Diffusion coefficient is the proportionality factor D in Fick's law (see Diffusion) by which the mass of a substance dM diffusing in time dt through the surface dF normal to the diffusion direction is proportional to the concentration gradient grad c of this substance: dM = −D grad c dF dt. Hence, physically, the diffusion coefficient implies that the mass of the substance diffuses through a unit surface in a unit time at a concentration gradient of unity. The dimension of D in the SI system is a square meter per second.
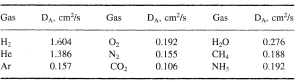
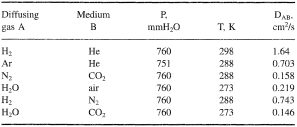
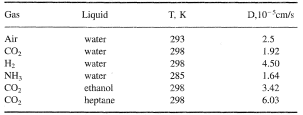
The diffusion coefficient is a physical constant dependent on molecule size and other properties of the diffusing substance as well as on temperature and pressure. Diffusion coefficients of one substance into the other are commonly determined experimentally and presented in reference tables. Here, examples of self-diffusion and interdiffusion (binary diffusion) coefficients in a gaseous and liquid media are given in Tables 1, 2, and 3.
As is obvious from comparing the data of Tables 1 and 2 with those of 3, the diffusion coefficients in a gaseous and a liquid phases differ by a factor of 104 − 105, which is quite reasonable considering that diffusion is the movement of individual molecules through the layer of molecules of the same substance (self-diffusion) or other substances (binary diffusion in which the molecules of two substances interdiffuse). The number density of molecules in liquid is also very much higher and their mobility is lower, which implies a much lower diffusion coefficient In solids, diffusion is still slower.
If experimental data are lacking, the diffusion coefficient can be calculated.
Diffusion in gases. For ideal gases, the diffusion coefficient does not depend on substance concentration. In accordance with the kinetic theory of gases, the mean free-path length l of molecules is inversely proportional to the mean cross-sectional area of the molecule S and the number density of the molecules n in a mixture. The latter is inversely proportional to the space occupied by the mixture, i.e., T/p, where T is the temperature and p, the pressure. The mean velocity of the molecules u is proportional to
 , where
, where
 is the molecular mass. Thus, in the case of interdiffusion of gases with the same molecular mass μ, or self-diffusion, the expression is:
is the molecular mass. Thus, in the case of interdiffusion of gases with the same molecular mass μ, or self-diffusion, the expression is:

If molecules of types A and B interact (binary diffusion), then the interdiffusion coefficient is:

where SAB is the mean value of the cross-sections of molecules of both types. The kinetic theory of gases makes it possible to determine the constant in Eq. (1), assuming the molecules are spherical and their cross-sections are equal to cross-sections of these spheres.
Sutherland has made a correction to Eq. (1), taking into account the forces of intermolecular attraction which influence the free-path length of molecules; thus,
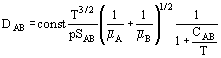
where CAB is the Sutherland coefficient.
Contemporary kinetic theory takes into account the intricate character of molecular interaction; molecules repel one another when they are close and attract one another at a distance. Many researchers have studied the potentials of this molecular interaction, but great recognition has been won by the so-called Lennard-Jones potential

where φ(r) is the potential energy; r, the distance between the centers of molecules; ε and σ are Lennard-Jones' interaction constants determined for many gases and summarized in tables.
For dilute gas mixtures, and assuming that the molecular collisions are only binary and elastic, that the motion of colliding molecules is in terms of classical mechanics, that quantum effects are absent, and, finally, intermolecular forces act only along the center line, the expression

for the diffusion coefficient in a binary mixture is obtained by Bird, Hirshfelder and Curtiss. Here, Ω = f(kT/εAB) is the collision integral and k is the Boltzmann's constant. The interaction parameters εAB and σAB determined for the binary system from the appropriate constants for pure substances:

If the data on ε and σ are not available, they can be estimated using the well-known critical parameters for a given substance:

where Tc and Vc are the critical temperature (K) and the critical molar volume (cm3/mol), respectively.
Wilke and Lee noted the coefficient 1.885Ч10−2 is not constant in reality and depends on molecular masses of the diffusing gases:
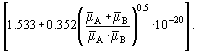
This accurate definition results in a better agreement between experimental and computed data.
A correlation formula obtained by Fuller, Schetter and Gittings by means of computer-aided correlation of 340 experimental points, expressed as:

has come to be widely known, where (∑ VA) and (∑ VB) are the values derived from summation of atomic diffusion volumes for each component of the binary mixture, i.e., molecules A and B. The values for some atoms and simple molecules are presented in Table 1.
In order to calculate the diffusion coefficient in multicomponent systems, Wilke used the Maxwell-Stefan equation to derive the expression

where D'A is the diffusion coefficient of the component A in the mixture with B, C, ..., YA, YB, YC are the molar fractions of the appropriate components; and DAB and DAC are the diffusion coefficients in the AB and AC binary systems, respectively.
Diffusion in liquids. As has been noted, diffusion in liquids encounters greater resistance and the diffusion coefficients for liquids lower than 104 to 105 times.
One of the earliest equations for determining the diffusion coefficient in dilute solutions was the Stokes-Einstein equation, based on the model of motion of a spherical particle of diffusing substance A in a viscous liquid continuum B

where r0 is the particle (molecule) radius and ηB, the liquid viscosity. The constant b depends on the size of diffusing molecules: b = 6 for molecules larger than those of the base substance; b = 4 for identical molecules; and b can be less than 4 for smaller molecules.
Assuming that the molecule diameter
 , where
, where
 is the molar volume of a diffusing substance and N0 is the Avogadro number, then
is the molar volume of a diffusing substance and N0 is the Avogadro number, then

Comparison of this formula with experimental data has shown that in most cases, the discrepancy is moderate and reaches 40% only in some cases.
In 1955, Wilke and Chang have suggested a more general formula based on extensive experimental investigations, but involving many empirical values as well

where DAB is the interdiffusion coefficient in an infinitely-dilute solution, cm2/s; φ, the parameter of association of solvent B;
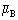 , the molecular mass of substance B;
, the molecular mass of substance B;
 , the molar volume of solute A at a boiling point under normal conditions, cm3/mol; ηB, the substance viscosity, Ns/m2; and T, the temperature, K.
, the molar volume of solute A at a boiling point under normal conditions, cm3/mol; ηB, the substance viscosity, Ns/m2; and T, the temperature, K.
Introduction of the association parameter into the formula is brought about by the fact that associated molecules behave like large-size molecules and diffuse at a lower rate; the degree of association varying with mixture composition and with molecule types. Therefore, Wilke and Chang presented the values for most widespread solvents: for water φ = 2.6; methanol, 1.9; ethanol, 1.5; benzene, ester, heptane and nonassociated solvents, 1.
A semiempirical formula suggested by Scheibel,

is worthy of attention. In some cases, it appears to be more exact than the preceding one; but for vA/vB ≤ (1 - 2), the deviation from experiment becomes important and the following relations are recommended:


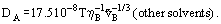
Reddy and Doraiswamy have suggested the equation
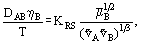
where KRS varies depending on the ratio of molar volumes: KRS = 8.5 10−8 for
 and KRS = 10−7 for
and KRS = 10−7 for
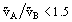 . Comparison of this equation with 96 experimental points has shown good agreement, the spread of points being about +15%.
. Comparison of this equation with 96 experimental points has shown good agreement, the spread of points being about +15%.
All formulas suggested above for calculating the diffusion coefficient hold true for low-viscosity liquids. For a high-viscosity solvent, they are in great error and therefore inapplicable.
The temperature effect on the diffusion coefficient has been poorly studied so far. Within a narrow temperature range—from 10 to 20°C—the temperature dependence of the diffusion coefficient can be assumed to be linear

where D298 is the diffusion coefficient at T = 298K,
 ; η298, the solvent viscosity at T = 298K, Ns/m; ρ, the solvent density, g/cm3.
; η298, the solvent viscosity at T = 298K, Ns/m; ρ, the solvent density, g/cm3.
Theoretically, this must be an exponential dependence of the type D = AT exp (-E/RT).
The experimental data of Wilke and Chang give available evidence that the activation energy varies from 12.6 to 28.1 kJ/mol.
The dependence of the diffusion coefficient on concentration of diffusing substance, strictly speaking, is a consequence of the fact that diffusion flow depends on the difference (gradient) of the thermodynamic potential of the system rather than concentration, i.e., the formula must allow for activity of the diffusing substance. Hence, at VB = const,

where D0 and D are the diffusion coefficients, respectively, in an infinitely-dilute solution and in a solution with finite concentration c; a and c, the activity and the concentration of diffusing substance; and n, the activity coefficient of this substance. The semiempirical formulas presented above are more exact than the theoretical ones because the latter were derived making assumptions. Nevertheless, to avoid an appreciable error it is advisable to make calculations by several formulas concurrently and to compare the results.
In electrolyte solutions, salts dissociate and diffuse as ions and molecules depending on the degree of dissociation. The theory of salt diffusion is elaborated mainly for dilute solutions in which the degree of dissociation is close to one. Thus, the diffusion coefficient for a simple salt that is infinitely diluted can be found using the Nernst-Heckell equation

where DAB is the diffusion coefficient, defined as the proportionality factor between the molecular flow of dissolved salt and the gradient of its molecular concentration, cm2/s; T, the temperature, K; Fa, the Faraday number, n+ and n-, the cation and anion valences;
 and
and
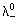 , the limit (under an infinite dilution) ionic conductions of cation and anion, cm2/Ω mol.
, the limit (under an infinite dilution) ionic conductions of cation and anion, cm2/Ω mol.
In electrolyte solutions, the diffusion coefficient substantially depends on the concentration of diffusing substance. If its concentration is no more than 2N, the formula
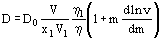
is suggested by Gordon, where D0 and D are the diffusion coefficients for an infinitely dilute solution and a molar solution, respectively; V, the solution volume; V1, the partial volume of the solvent; x1, the number of solvent moles in volume V; ν, the molarity of the solution; η and η1, the viscosity of solution and solvent; v, the molar activity coefficient.
REFERENCES
Hirschfelder, J. O., Curtiss, C. F., and Bird, R. B. (1954) Molecular Theory of Gases and Liquids, Wiley, New York.
Sherwood, T. K., Pigford, R. L., and Wilke, C. R. (1975) Mass Transfer, McGraw Hill, New York.
Использованная литература
- Hirschfelder, J. O., Curtiss, C. F., and Bird, R. B. (1954) Molecular Theory of Gases and Liquids, Wiley, New York. DOI: 10.1126/science.120.3131.1097
- Sherwood, T. K., Pigford, R. L., and Wilke, C. R. (1975) Mass Transfer, McGraw Hill, New York.