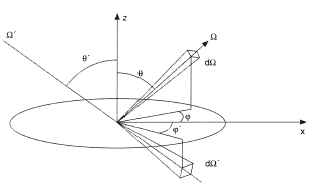
Emissivity (ε) is a measure of the ability of media to emanate thermal radiation (i.e., electromagnetic radiation in the wavelength range 10–1 to 102 μm) relative to radiation emanation from an ideal “black body” of a similar temperature.
In the general case, emissivity is determined using radiation spectral intensity —the electromagnetic radiation energy propagating inside a unit solid angle in the
—the electromagnetic radiation energy propagating inside a unit solid angle in the  -direction through a unit area at a unit time in a unit spectral range.
-direction through a unit area at a unit time in a unit spectral range.
For reference, black body spectral intensity Ib,w(T) is used which is given by:

Here, the units of Ib,w(T) are W/(cm2·micron).
The effective directional spectral intensity of a surface at distance  from the surface is a result of the directional intensity of self-radiation
from the surface is a result of the directional intensity of self-radiation  and reflected radiation
and reflected radiation  (Figure 1):
(Figure 1):

In local thermodynamic equilibrium, the effective directional spectral intensity  is given by:
is given by:
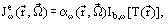
where  is the directional absorptivity.
is the directional absorptivity.
The spectral intensity of the reflected radiation is represented as:

where  is the spectral intensity of the radiation incident on a surface element
is the spectral intensity of the radiation incident on a surface element  in the
in the  -direction, and
-direction, and  is the spectral distribution function of the reflected radiation. For the particular cases of mirror-like and isotropically reflecting surfaces, the angle-dependence of the distribution function for the reflected radiation is supposed to be taken in the form of the δ-function, or constant. The directional spectral emissivity of any real surface at fixed temperature is always less than the intensity of radiation emanated by a black-body surface at the appropriate temperature and wave number.
is the spectral distribution function of the reflected radiation. For the particular cases of mirror-like and isotropically reflecting surfaces, the angle-dependence of the distribution function for the reflected radiation is supposed to be taken in the form of the δ-function, or constant. The directional spectral emissivity of any real surface at fixed temperature is always less than the intensity of radiation emanated by a black-body surface at the appropriate temperature and wave number.
The ratio

is called spectral emissivity.
If the Kirchhoff law holds, then  .
.
The spectral hemispherical emissivity is of the form

The total hemispherical emissivity is:

The spectral emissivity of the effective surface radiation is determined in a similar way when replacing  by
by 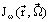 in Eqs. (5) and (6).
in Eqs. (5) and (6).
The directional spectral intensity from a volume element is defined by the relation
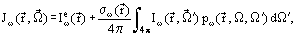
where  is the self-radiation intensity. Both
is the self-radiation intensity. Both  and
and  have the units of energy per unit volume per unit time into a unit solid angle in a unit spectral range:
have the units of energy per unit volume per unit time into a unit solid angle in a unit spectral range:  and
and  are the spectral scattering coefficient and spectral phase function of the radiation incident to a unit volume characterized by
are the spectral scattering coefficient and spectral phase function of the radiation incident to a unit volume characterized by  in the
in the  -direction. The self-radiation energy is emanated isotropically, therefore
-direction. The self-radiation energy is emanated isotropically, therefore  depends on the location of the elementary volume only. If the approximation of local thermodynamic equilibrium is valid, then the intensity of self-radiation
depends on the location of the elementary volume only. If the approximation of local thermodynamic equilibrium is valid, then the intensity of self-radiation 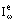 is expressed in terms of the spectral intensity of the black-body radiation according to Kirchhoff’s law
is expressed in terms of the spectral intensity of the black-body radiation according to Kirchhoff’s law

where  is the volumetric spectral absorption coefficient.
is the volumetric spectral absorption coefficient.
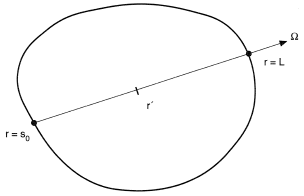
In a given medium volume, the spectral emissivity of the beam segment [s0, L] in a fixed direction (see Figure 2) is determined when solving the transfer equation. This solution can be expressed formally as:

where

It is assumed that the radiation does not reach the boundary r = s0 . When there is no light scattering and the medium properties are constant on the entire segment (i.e., the optical path is uniform) the spectral radiation intensity is expressed as:

The hemispherical (or total) emissive power which is a radiation flux density on the base of hemispherical uniform volume of the R radius is the most widely-used quantity and is of the form

The spectral emissive power of a plane layer characterizes the radiation flux density on the boundary of a uniform plane layer of H thickness

where E3(t) is an integro-exponential function of the third order. It has been shown by numeruous investigations that the emissive power of uniform volumes of various geometries can be approximately calculated using the hemispherical emissive power E(R) when an equivalent radius is given.
Like surface spectral emissivity, the concept of a spectral emissivity for a hemispherical volume is introduced

as well as that of a plane layer

and for other volumes. The physical meaning of spectral emissivity is a ratio of the spectral radiation flux density on the volume boundary to that of a black-body.
In the case of small optical thickness 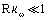 the following approximate relation for the spectral emissivity of a uniform flow holds
the following approximate relation for the spectral emissivity of a uniform flow holds

The total and group emissive power (directional, hemispherical, plane layer, etc.) are obtained by integrating the spectral emissive power over the entire range of wave numbers or over an isolated spectral interval, respectively:

In a similar way, total and group emissivities are defined, e.g., for a semispherical volume and plane layer:

To calculate total and group emissive power for volumes of various geometries, one needs to know the volumetric spectral absorption coefficient  which is, as a rule, a very complicated function of the radiation wave number with variations of an order of magnitude and with rapidly-oscillating spectral dependence due to monatomic and molecular absorption.
which is, as a rule, a very complicated function of the radiation wave number with variations of an order of magnitude and with rapidly-oscillating spectral dependence due to monatomic and molecular absorption.
Due to the complicated spectral dependence of the absorption coefficient, there are essential difficulties in calculating group and total emissive power even where there is no light scattering. For gases frequently used in engineering practice (air, CO2 and H2O), detailed experimental and theoretical results are classified in tabular and graphic data on spectral hemispherical emissive power [Siegel and Howell (1972); Ozisik (1973); Ludwig, Malkmus, and Reardon et al. (1973)].
If a line structure manifests itself only weakly in the absorption coefficient spectrum, emissive power can be calculated efficiently by group approximation. The spectral range under investigation is divided into a number of intervals (spectral groups) inside of which each of the spectral coefficient is assumed to be independent of the radiation wave number. In this case, the total emissive power is represented as a sum

where NΔω is the number of spectral groups, κΔω,l is the mean absorption coefficient of each interval, Δωl, and Ib,Δωl = ∫Δωl Ib,ω(T) dω. This approach gives satisfactory results for the line spectrum as well if conditions for full line overlapping are implemented and the spectrum practically becomes continuous.
To describe the spectrum line structure, the group approach may also be used. But within each spectral group, the absorption coefficient is no longer a constant value and models of the molecular line bands are used [Siegel and Howell (1972); Ozisik (1973); Ludwig, Malkmus, Reardon et al. (1973); Rodgers and Williams (1974); Goody (1964); Penner (1959); Edwards and Menard (1964); Tien (1968)]. When taking into account statistical models, the total emissive power is represented as:





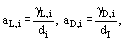
where Nb,l is the number of spectral line bands in a spectral range Δωl; Wi(L – s0) is the equivalent thickness of i-th spectral line band for a Voigt contour, WL,i; WD,i is the equivalent thickness for the Lorentz and Doppler contour; ki,l is the averaged absorption coefficient in the i-th line band of a spectral range 1; γL,i and γD,i are the line half-width widened by collision (the Lorentz profile) and the Doppler widening mechanisms; and di is the line density in the i-th band. In obtaining Eq. (20), a statistical model with exponential distribution of line intensities is used as well as methods that approximate equivalent length. For other approximation methods see Ludwig et al. (1973), Goody (1964), Penner (1959), Edwards and Menard (1964) and Tien (1968).
There are many methods to group lines in a band; the simplest one is to combine all the lines of the gas component into one band. Then Nb,l Eq. (20) is the number of gas mixture components which have lines in the range Δωl .
The numerical and experimental results on kl,i and di are given as tables by Ludwig et al. (1973) (CO, NO, CN, OH, HC1, HF, CO2, H2O) and in the form of approximations by Siegel and Howell (1972) and Tien (1968) (CO2, CH4, H2O, CO).
The method of line-by-line integration is also sometimes used, with the spectral range divided into thousands and tens of thousands of intervals to describe in detail the absorption in each line. Such laborous calculations are performed to obtain basic results which are compared with the results obtained by approximate methods.
In the case of scattering, the problem of determining emissive power becomes more complicated since it is necessary to find the scattering coefficients  and the phase functions
and the phase functions 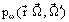 . For this the Mie theory, geometrical optics approximation and the Rayleigh theory [Bohren and Huffman (1983)] are used as well as solutions of the integro-differential radiation transfer equation. The general effect of radiation scattering on emissive power is to diminish it, and this usually occurs if the albedo is sufficiently high
. For this the Mie theory, geometrical optics approximation and the Rayleigh theory [Bohren and Huffman (1983)] are used as well as solutions of the integro-differential radiation transfer equation. The general effect of radiation scattering on emissive power is to diminish it, and this usually occurs if the albedo is sufficiently high

The determination of emissive power in a nonequilibrium medium hinges on solving kinetic equations which determine the population of excited states of radiating particles and which calculate the probabilities of radiation transition from highly-excited energetic states to lower ones. The relation between emissive power and volumetric absorption coefficients as in Eq. (9) is inapplicable here.
The total amount of spectral, group or total radiation energy emitted from a volume of a medium per unit time in all directions over the solid angle 4π is the total emissive power.
REFERENCES
Bohren, C. F. and Huffman, D. R. (1983) Absorption and Scattering of Light by Small Particles, A Wiley-Interscience Publication. John Wiley & Sons, Inc.
Edwards, D. K. and Menard, W. A. (1964) Comparison of models for correlation of total band absorption. Applied Optics. 3: 621–625.
Goody, R. M. (1964) Atmospheric Radiation. I. Theoretical Basis. Oxford, At the Clarendon Press.
Ludwig, C. B., Malkmus, W., Reardon, J. E. et al. (1973) Handbook of Infrared Radiation from Combustion Gases. Washington: NASA SP—3080: 486.
Ozisik, M. N. (1973) Radiative Transfer and Interaction with Conduction and Convection. A Wiley-Interscience Publication.
Penner, S. S. (1959) Quantitative Molecular Spectroscopy and Gas Emissivities. Addison-Wesley, Reading, MA. DOI: 10.1016/0016-0032(60)90912-1
Rodgers, C. D. and Williams, W. (1974) Integrated absorption of a spectral line with the Voigt Profile. JQSRT. 14(4) 319–323. DOI: 10.1016/0022-4073(74)90113-7
Siegel, R. and Howell, J. R. (1972) Thermal Radiation Heat Transfer. McGraw-Hill, New York.
Tien, C. L. (1968) Thermal radiation properties of gases. in Advances in Heat Transfer. 5. Academic Press, New York.
Referências
- Bohren, C. F. and Huffman, D. R. (1983) Absorption and Scattering of Light by Small Particles, A Wiley-Interscience Publication. John Wiley & Sons, Inc.
- Edwards, D. K. and Menard, W. A. (1964) Comparison of models for correlation of total band absorption. Applied Optics. 3: 621–625.
- Goody, R. M. (1964) Atmospheric Radiation. I. Theoretical Basis. Oxford, At the Clarendon Press. DOI: 10.1002/qj.49709138722
- Ludwig, C. B., Malkmus, W., Reardon, J. E. et al. (1973) Handbook of Infrared Radiation from Combustion Gases. Washington: NASA SP—3080: 486.
- Ozisik, M. N. (1973) Radiative Transfer and Interaction with Conduction and Convection. A Wiley-Interscience Publication. DOI: 10.1002/aic.690210139
- Penner, S. S. (1959) Quantitative Molecular Spectroscopy and Gas Emissivities. Addison-Wesley, Reading, MA. DOI: 10.1016/0016-0032(60)90912-1
- Rodgers, C. D. and Williams, W. (1974) Integrated absorption of a spectral line with the Voigt Profile. JQSRT. 14(4) 319–323. DOI: 10.1016/0022-4073(74)90113-7
- Siegel, R. and Howell, J. R. (1972) Thermal Radiation Heat Transfer. McGraw-Hill, New York.DOI: 10.1002/aic.690180243
- Tien, C. L. (1968) Thermal radiation properties of gases. in Advances in Heat Transfer. 5. Academic Press, New York.