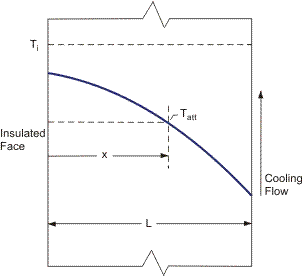
The Fourier Number (Fo) is a dimensionless group which arises naturally from the nondimensionalization of the conduction equation. It is very widely used in the description and prediction of the temperature response of materials undergoing transient conductive heating or cooling. The significance of the Fourier Number may be exemplified by considering a simple case of one-dimensional conduction. Figure 1 shows an instantaneous temperature profile at some time t during the cooling of a plate, which was initially at temperature Ti throughout, has one side insulated
 and the other side exposed to some cooling environment. In the absence of any internal energy conversion processes the conduction equation for this system (see Conduction) simplifies to:
and the other side exposed to some cooling environment. In the absence of any internal energy conversion processes the conduction equation for this system (see Conduction) simplifies to:

where κ is the thermal diffusivity of the material (λ/ρcp). The solution of this equation yields the required information on the spatial temperature distribution at any time t, as represented by the curve in Figure 1.
When a problem is posed in dimensionless form, the resulting solution is widely applicable to other problems in the same class. With transient conduction problems a dimensionless form of the conduction equation is easily obtained by scaling the dependent and independent variables using some convenient and constant system parameters. Choosing the initial, constant, temperature (Ti) and the plate width (L), a dimensionless temperature (θ = T/Ti) and dimensionless position (X = x/L) can be defined so that the conduction equation is transformed to:

To complete the nondimensionalization process a dimensionless time. κt/L2, the Fourier Number, is introduced so that the completely dimensionless form of the conduction equation becomes:
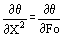
Solutions to transient conduction problems are often presented with a dimensionless temperature expressed as a function of Fourier Number [see Rohsenow et al. (1985)].
REFERENCES
Rohsenow, W. M., Hartnett, J. P. and Ganic, E. N. (1985) Handbook of Heat Transfer, 2nd ed., McGraw-Hill, New York.
Referencias
- Rohsenow, W. M., Hartnett, J. P. and Ganic, E. N. (1985) Handbook of Heat Transfer, 2nd ed., McGraw-Hill, New York.