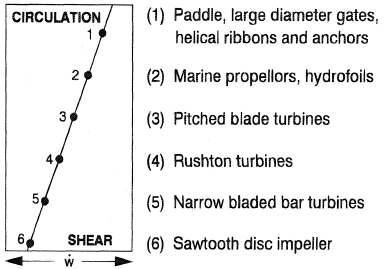
Impeller mixers are simple but versatile equipment used widely in the process industries to mix a liquid with another liquid, a gas or solids using forced convection (flow). A variety of impeller designs is available but their classification is not unique. Clearly the viscosity of the mix for which the impeller is intended is an important consideration and can be used as a first broad basis for classification. Low viscosity fluids are usually processed by small impellers but highly viscous fluids require comparatively bulkier impeller designs. A typical example is the distinct physical difference between a propeller and a helical ribbon impeller. Other bases, relating also to flow, are the way in which impellers generate flow (by shear stress or pressure) and the types of flow pattern they produce (tangential, radial, or axial). Paddle, turbine and propeller impellers, for example, transmit momentum by direct pressure of the blades on the liquid but a rotating disk impeller instead shears the liquid. A marine type mixing propeller will generate axial flow whereas a flat blade turbine generate a radial flow and some designs produce mixed radial and axial flows. An example of this classification is illustrated in Figure 1 and further details are given by Starbacek and Tausk (1965) and Zlokarnik and Judat (1988). From a hydrodynamic point of view, impeller mixers resemble pumps in which a power input,
 , is expended for the circulation of the liquid (pumping capacity,
, is expended for the circulation of the liquid (pumping capacity,
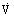 ) and the generation of shear as a result of the hydrodynamic head, Z, developed giving:
) and the generation of shear as a result of the hydrodynamic head, Z, developed giving:

where ρ is the density of the liquid. Consequently, impeller mixers can also be classified on the basis of their typical power input requirement (see Table 1) and ability to produce at a constant power input the required balance of flow circulation and shear as illustrated in Figure 2 and described further by McDonough (1992).
For example, dispersion of immiscible liquids and of solid agglomerates in liquids will be more effectively carried out in high shear devices whereas the blending of liquids will require axial flow impellers which are capable of producing high flow. Clearly, the power and flow-head characteristics of an impeller mixer are basic design and operation information. Because of the large number of variables involved in an impeller mixer system and the way in which the flow is induced, it is theoretically not yet possible to predict these characteristics (although much progress has been made in recent years with computational fluid dynamics). Experiments become necessary and are carried out usually with liquids in well baffled vessels (to prevent vortexing which hinders mixing) on a laboratory scale for application to a large scale.
Typically, experiments are carried out in cylindrical vessels filled with liquid to a height equal to the diameter of the vessel. The principal variables become: the impeller diameter, Di, and its rotational speed, ω (rev/s), the vessel diameter and the physical properties of the liquid (its density, ρ, and viscosity, η). For each impeller-vessel system there will also be a number of dimensions defining the geometrical arrangement. Measurements of power,
 , and flow circulation,
, and flow circulation,
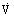 , are taken over a range of conditions and Dimensional Analysis principles are used to correlate the data which are expressed as power number, Nw =
, are taken over a range of conditions and Dimensional Analysis principles are used to correlate the data which are expressed as power number, Nw =
 /
/
 and circulation rate number, Nv =
and circulation rate number, Nv =
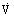 /
/
 as functions of the Reynolds Number, Re =
as functions of the Reynolds Number, Re =
 and the impeller vessel geometrical ratios which are numerous. In addition to these basic measurements, a tracer can be dropped in the liquid and a mixing time, t, evaluated and expressed as a mixing time number, Nt = ωt. It too is a function of the Reynolds number and impeller-vessel geometrical ratios.
and the impeller vessel geometrical ratios which are numerous. In addition to these basic measurements, a tracer can be dropped in the liquid and a mixing time, t, evaluated and expressed as a mixing time number, Nt = ωt. It too is a function of the Reynolds number and impeller-vessel geometrical ratios.
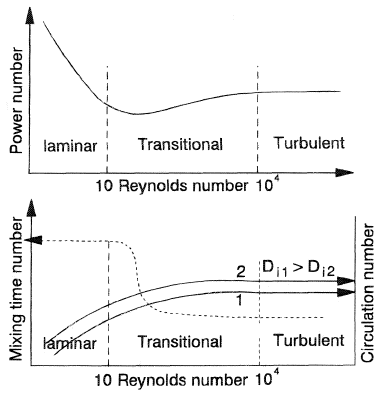
Some key observations can be made on these functions as illustrated in Figure 3. As expected, the Reynolds number which controls the nature of the flow is the dominant variable. We observe a unique relationship between Nw and Re in both the laminar (Nw = constant/Re) and turbulent (Nw = constant) regimes. The same holds with the mixing time and flow circulation numbers showing the beneficial effect of turbulence on mixing, but the geometry of the impeller in relation to the vessel also has an influence particularly on the pumping capacity-shear characteristics. In general, for a given power level, high circulation and low shear are observed with large impeller diameter running at low speeds. Small diameter impellers running at high speeds usually produce low circulation but intense shearing. An axial flow turbine shows typically:

The literature abounds with correlations and graphs which relate Nw, NV, Nt to Re and geometrical ratios [see, for example, Nagata (1975) and Uhl and Gray (1975]. When using these data, care must be taken in identifying the applicable geometrical ratios. This is very important when considering scale-up of equipment. Of course, scaling up cannot be based on geometry alone, kinematic (relating to velocities and flow patterns) and dynamic (relating to forces) similarities must also be taken into account. A number of scale-up criteria can result (see Table 2) but unfortunately not all similarities hold as they usually conflict with each other and a consideration of the important physical aspects of the operation become necessary. Even then, an intermediate scale-up prior to full scale design may be necessary. These considerations are clearly very important and are addressed in most of the references cited. All the treatment discussed so far applies strictly to a single Newtonian liquid. It forms however a fundamental basis for analyzing mixing in the more complex situations where often all that is required is an impeller mixer delivering the correct balance of flow and shear at minimum energy input.
REFERENCES
McDonough, R. J. (1992) Mixing for the Process Industries, Van Nostrand, Reinhold, New York.
Nagata, S. (1975) Mixing: Principles and Application, John Wiley & Sons, Inc., New York.
Sterbacek, Z. and Tausk, P. (1965) Mixing in the Chemical Industry. Pergamon Press, Oxford.
Uhl, V. W. and Gray, J. B. (1966) Mixing Theory and Practice, Academic Press.
Zlokarnik, M. and Judat, H. (1988) Stirring, in Ullmann’s Encyclopedia of Industrial Chemistry, 5th Edn., Vol. B2.
References
- McDonough, R. J. (1992) Mixing for the Process Industries, Van Nostrand, Reinhold, New York.
- Nagata, S. (1975) Mixing: Principles and Application, John Wiley & Sons, Inc., New York.
- Sterbacek, Z. and Tausk, P. (1965) Mixing in the Chemical Industry. Pergamon Press, Oxford.
- Uhl, V. W. and Gray, J. B. (1966) Mixing Theory and Practice, Academic Press.
- Zlokarnik, M. and Judat, H. (1988) Stirring, in Ullmann’s Encyclopedia of Industrial Chemistry, 5th Edn., Vol. B2.