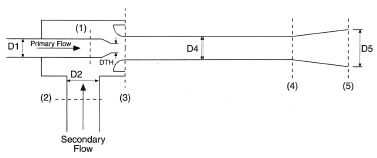
Ejectors, or jet pumps, utilize the pressure energy of a high-pressure fluid stream to boost the pressure and/or flow of a low-pressure source. They can operate with either incompressible or compressible fluids as the primary (driving) and secondary (driven) flows. The main features of an ejector are shown in Figure 1 . The figure also defines the subscripts used later for primary (1), secondary (2), etc.
The primary fluid is passed through a nozzle where the pressure energy is converted into kinetic energy. The high-velocity jet entrains the secondary fluid. The two streams mix in the mixing tube, leading to pressure recovery. Further static pressure is recovered in a narrow-angle diffuser downstream of the mixing tube.
Ejectors are generally inefficient devices. However, their simplicity and lack of moving parts make them worthy of consideration, particularly where a high-pressure stream of fluid is already available. Table 1 summarizes potential ejector applications.
Note that the term 'Jet Pump' is used to refer to a liquid—liquid ejector.
The most comprehensive source of design information for ejectors can be found in a series of Engineering Sciences Data Unit (ESDU) data items, Nos. 85032 and 84029. These are available on subscription as part of the ESDU Internal Flow series.
Three key parameters for a jet pump are the pressure ratio, defined by

where P1, etc. are total pressures, as indicated in Figure 1 ,
the flow ratio

and the ratio of mixing tube-to-nozzle diameter (R). These are related through the equation

where C is the density ratio (secondary to primary). The loss coefficients Kp, Ks, Km and Kd account for losses in the primary nozzle, secondary flow inlet, mixing chamber and diffuser, respectively. For high Reynolds number applications (above 2 × 105), values of 0.05,0.1,0.15 and 0.2 can be assumed for a well-designed jet pump.
The equation can be solved directly for N if C, M and R are known. Alternatively, either graphical (e.g., ESDU 85032) or equation solving methods can be used.
Ejector efficiency can be calculated from

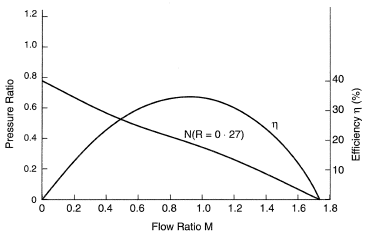
Figure 2 shows a typical efficiency and performance curve for a jet pump, as a function of secondary flow rate. Note the typical shape, with a peak efficiency of around 35%.
For a particular application (i.e., given primary and secondary flows/pressures), an optimum value of R can be found by trial and error.
Once the ratios have been determined, the primary nozzle can be sized from

For a well-designed nozzle, a value of 0.95 for discharge coefficient (CD) can be used. The nozzle should be conical with a half-angle of 5-10°. A parallel section at the nozzle outlet (see Figure 1) is not critical to performance, but can improve the mechanical strength of the design.
Entry to the mixing tube needs to avoid large secondary flow losses: either a converging conical section or a bell-mouth entry should be used. A mixing tube length of 7-10 (mixing tube) diameters is recommended.
To reduce downstream pressure losses, the flow needs to be expanded downstream of the mixing tube to lessen flow velocities to a reasonable level. As this may involve a large area ratio, a narrow angle diffuser is required (typically 2-3° half angle).
When operating at low suction pressures and high flow ratios, cavitation can prove to be a problem with jet pumps. Detailed information is available in Cunningham et al. (1969) or ESDU 85032.
For small pressure differences, gas-gas ejectors can be treated like liquid jet pumps. However, for higher pressure ratios, compressibility effects need to be taken into account. Above a critical pressure ratio between primary and secondary (around 1.8, depending on gas properties), flow in the primary nozzle reaches sonic velocity. Flow in the nozzle becomes independent of secondary pressure, and is given by;

where CD is the discharge coefficient, STH the throat area, γ the ratio of specific heat at constant pressure to the specific heat at constant volume and R, the specific gas constant. (See Critical Flow, Jets and Nozzles.)
Downstream of the nozzle, flow will expand in a series of supersonic shocks until the pressures of both streams become equal and mixing occurs.
In some ejector designs, a converging-diverging nozzle is utilized to accomodate the expanding jet. An 'on-design' condition can be defined where the static pressures of primary and secondary flows are equal at the nozzle exit. However, work by Ashton, Green and Reade (1993) suggests that the use of a diverging section is not necessary for effective operation, at least at moderate pressure ratios. Performance can be then calculated by considering conservation of mass, momentum and energy in the mixing tube and diffuser. Owing to the complexity of the equations, these cannot be solved directly. A complex graphical method is available in ESDU 84029.
As with a jet pump, the key geometric factor in the design is the mixing tube diameter. Performance increases by reducing mixing tube diameter up to a point where the expanding supersonic primary jet almost fills the mixing tube before mixing can take place and choking occurs. A further decrease in mixing tube diameter (or any attempt to increase secondary flow) causes performance to decrease rapidly.
Design requirements for the nozzle, mixing tube and diffuser are similar to those for jet pumps.
These ejectors utilize liquid as the primary fluid: generally, gas-driving liquid is not a very effective arrangement due to differences in density (and hence momentum) between the streams. Performance can be generally characterized by an equation of the form

where G and L refer to the gas and liquid, respectively and VLmin is a minimum value of liquid flow below which no gas flow will occur. An expression for VLmin has been derived by Henzler (1980), given by:

Given the different densities of the two streams, mixing duty tends to be more arduous than in a single-phase ejector, and generally longer mixing tubes than those for single-phase ejectors are used (typically 20-30 diameters). However, where mixing does occur, this is very intensive (the 'mixing shock'). This tends to result in significant energy losses. A spinner upstream of the primary nozzle is sometimes used to help disintegrate the jet and induce early mixing.
Gas-liquid ejectors can be very effective devices for mass transfer applications. They can be used either as stand-alone devices, or in combination with a contact vessel. They have the combined benefits of being able to draw in gas without the need for compression, and providing a very fine dispersion in the mixing tube.
Ejectors are characterized by cocurrent plug flow in the mixing tube, with very high energy dissipation rates (typically in the range 100-1,000 W/kg), but short residence times (less than 1 second). This leads to mass transfer coefficients typically 2-3 orders of magnitude greater than a typical stirred tank, making them particularly suited to absorption with rapid, competing chemical reactions where fast mixing is required to reduce byproduct formation.
Where longer residence time is required, ejectors are often combined with a contact vessel. In such cases, the ejector provides rapid initial mixing, a fine bubble dispersion and, if properly designed, good liquid mixing in the vessel. Gas can either be recycled, by using the suction characteristics of the ejector to draw gas back from the headspace of the vessel, or operated in once-through mode. The 'Buss Reactor,' successfully used for hydroginations, sulphonations, animations, etc. is designed on the former principle [e.g., see van Dierendonck and Leuteritz (1988)].
REFERENCES
Ashton, K. J., Green, A. J., and Reade, A. (1993) Gas Production Improvements Using Ejectors. SPE Paper 26684. Society of Petroleum Engineers.
Cunningham, R. G., Hansen, A. G., and Na, T. Y. (1969) Jet Pump Cavitation. Paper 69-WA/FE-29. ASME.
ESDU 84029 (1984) Ejectors and jet pumps. Design for compressible air flow. Engineering Sciences Data Unit.
ESDU 85032. (1984) Ejectors and Jet Pumps. Design and performance for incompressible liquid flow. Engineering Sciences Data Unit.
Henzler, H. J. (1980) Chem. Ing. Tech. 47: 5: 659 (in German).
van Dierendonck, L. L. and Leuteritz, G. M. (1988) Proc. Sixth Euro. Conf. on Mixing. Pavia. Italy. 287.
References
- Ashton, K. J., Green, A. J., and Reade, A. (1993) Gas Production Improvements Using Ejectors. SPE Paper 26684. Society of Petroleum Engineers.
- Cunningham, R. G., Hansen, A. G., and Na, T. Y. (1969) Jet Pump Cavitation. Paper 69-WA/FE-29. ASME.
- ESDU 84029 (1984) Ejectors and jet pumps. Design for compressible air flow. Engineering Sciences Data Unit.
- ESDU 85032. (1984) Ejectors and Jet Pumps. Design and performance for incompressible liquid flow. Engineering Sciences Data Unit.
- Henzler, H. J. (1980) Chem. Ing. Tech. 47: 5: 659 (in German).
- van Dierendonck, L. L. and Leuteritz, G. M. (1988) Proc. Sixth Euro. Conf. on Mixing. Pavia. Italy. 287.