The gas turbine is a turbine in which potential energy of heated and compressed gas is converted into kinetic energy as a result of its expansion in the tubine blading. Subsequently, the energy is converted into mechanical work on the rotating shaft. The process of expansion of the gas in a gas turbine takes place in one, or more often several, stages. As a rule, the total number of stages in a gas turbine is not large (not more than 3—5). In this aspect, gas turbines differ greatly from steam turbines (see Steam Turbine) in which the number of stages may reach several dozen. Reaction stages have higher efficiency than impulse stages and are therefore those mostly used in gas turbines. Either combustion products of organic fuels (liquid or gaseous) or clean air or other clean gases (for example, inert gases or their mixtures), heated in a special heat-exchanger heater, are used as the gas turbine working fluid. In the latter case, the clean air and other clean gases should not get mixed with the fuel combustion products. Mixtures of organic fuel combustion products with water or steam also can be used as gas turbine working fluids.
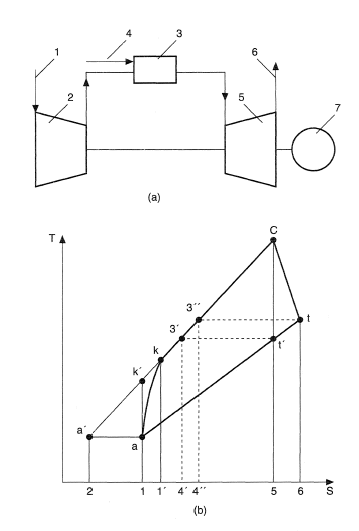
Gas turbines are usually components of gas turbine engines or gas turbine units. Therefore the term gas turbine often denotes both the gas turbine engine and the gas turbine unit. Here, only one term—a gas turbine unit—will be used whenever it does not result in the distortion of the meaning. In addition to the gas turbine, the simplest open-cycle gas turbine unit (see Figure 1a) consists of a compressor, 2, (see Compressor) with intake system, 1; combustion chamber, 3, (see Combustion Chamber); auxilliary systems (in particular the fuel feed system), 4. The air from the atmosphere passes from the intake system, 1, into the compressor, 2, where it is compressed and then delivered into the combustion chamber, 3, where the fuel is burnt. The combustion products (gas) enter the turbine, 5, and are expanded to a pressure close to atmospheric and after that they are exhausted into the atmosphere through the exhaust unit, 6. Some portion of the turbine power is used for driving the compressor, 2, for driving the auxiliary units (pumps, electric generators, mechanisms etc.) of the complete gas turbine unit and for overcoming hydraulic resistance in the gas turbine unit. The remaining power is used for driving the payload mounted on the turbine shaft, 7.
In all modern gas turbine units the process of heat input takes place at constant working fluid pressure in the combustion chamber, therefore these gas turbine units are defined as working through the cycle p = const.
Within the p = const gas turbine unit cycle the actual compression work in the "temperature-entropy" diagram (Figure 1b) is proportional to the area l'ka'2, adiabatic work lk0 is measured by the area lk'a'2'. Thus lk > lk0 and the difference lk – lk0 is proportional to the area lk'kl'. The predicted expansion work lt0 is proportional to the area 4'3'c5, the actual work of the turbine lt is measured by the area 4"3"c5. Therefore lt < lt0 and the difference lt0 – lt is proportional to the area 4'3'3"4". The specific useful work of the actual cycle is equivalent to the difference of areas l'kc5 and lat6. This difference is considerably smaller than the area akct, which is limited by the actual processes of the cycle (in the ideal cycle the work leid proportional to the area ak'ct' is limited by the ideal processes).
The specific useful work of the simplest gas turbine unit actual cycle le ≈ γRTa [ (1 – 1/χ) ηt – (χ – 11)], where R is the gas constant and γ is the adiabatic exponent for the process of compression in the compressor (or similar values for the expansion process in the turbine which are approximately assumed to be identical). Ta is the initial air temperature (corresponding to point "a", in Figure 1b);
(1 – 1/χ) ηt – (χ – 11)], where R is the gas constant and γ is the adiabatic exponent for the process of compression in the compressor (or similar values for the expansion process in the turbine which are approximately assumed to be identical). Ta is the initial air temperature (corresponding to point "a", in Figure 1b);  = Tc/Ta; Tc is the initial temperature of the combustion products (gas) (point "c"); χ = p(γ–1)/γ is a function of the pressure ratio π = pk/pa in the cycle and ηt and ηk are the efficiencies of the turbine and the compressor. The gas turbine unit capacity is
= Tc/Ta; Tc is the initial temperature of the combustion products (gas) (point "c"); χ = p(γ–1)/γ is a function of the pressure ratio π = pk/pa in the cycle and ηt and ηk are the efficiencies of the turbine and the compressor. The gas turbine unit capacity is  , where
, where  is the air (gas) flow rate through the compressor (the turbine). The simplest gas turbine unit cycle efficiency is
is the air (gas) flow rate through the compressor (the turbine). The simplest gas turbine unit cycle efficiency is

The cycle efficiency ηe as well as specific work le increases with the growth of  and with the efficiency of the turbine and the compressor. Approximate dependence of ηe (solid lines) and le (dashed lines) on π at Tc = 1000, 1100, 1200, 1300, 1500 K (curves 1, 2, 3, 4, 5) are given in Figure 2. Calculations were performed without taking into account losses connected with the turbine cooling. ηe and le grow considerably with the increase of Tc From the figure it also follows that it is necessary to increase π with the increase of
and with the efficiency of the turbine and the compressor. Approximate dependence of ηe (solid lines) and le (dashed lines) on π at Tc = 1000, 1100, 1200, 1300, 1500 K (curves 1, 2, 3, 4, 5) are given in Figure 2. Calculations were performed without taking into account losses connected with the turbine cooling. ηe and le grow considerably with the increase of Tc From the figure it also follows that it is necessary to increase π with the increase of  in order to employ the advantages connected with the increase of
in order to employ the advantages connected with the increase of  (or Tc). This is the current tendency of practical application of simple-cycle gas turbine units. The efficiency of such gas turbine units is not high (for example, for stationary industrial or heavy duty gas turbine units for power, ηe ≈ 28-33%).
(or Tc). This is the current tendency of practical application of simple-cycle gas turbine units. The efficiency of such gas turbine units is not high (for example, for stationary industrial or heavy duty gas turbine units for power, ηe ≈ 28-33%).
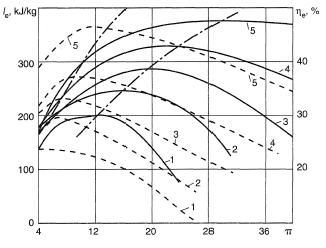
Figure 2. Variation of specific useful work le and unit efficiency ηe with π = Tc/Ta at various Te values.
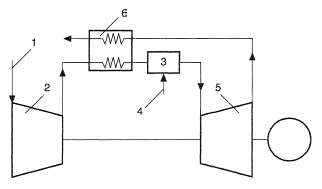
In the cycle of a regenerative gas turbine unit (Figure 3), the air entering through the intake system and compressed in the compressor, 2, passes into the heat exchanger, 6, where it is heated by gases issuing from the turbine, 5. The fuel flow rate, 4, in the combustion chamber, 3, can be decreased because the waste gas heat is used for heating the air. The advantage of schemes using heat regeneration is the possibility to maintain the efficiency of the unit practically constant and equal to the efficiency at design conditions in a wide range of loads (from 50 to 100%). The predicted efficiency of the turbine unit with regeneration at steady gas temperature Tc is higher than the efficiency of the simple-cycle gas turbine unit. Most gas turbine engines for wheeled vehicles and crawler-type vehicles are designed and constructed with the regenerative cycle because other possibilities of increasing the efficiency of these engines are rather limited.
For other types of gas turbine units, above all for stationary gas turbine units, regeneration is not applied in practice. This is connected with the large size of the heat-exchanger and with the necessity to use long and structually complicated piping systems, which causes additional hydraulic resistance. High specific power and efficiency (up to 50%) may be obtained in multicomponent gas-turbine units. In such plants, the value of p may be considerably higher (up to 22-55 and even 120) than in regenerative-type gas-turbine units. In simple-cycle gas-turbine units, the number of turbines and compressors is larger. However, they have no heavy and large-size regenerator and are less metal-intensive than regenerative-type gas-turbine units.
Closed-cycle gas-turbine units differ from the open-cycle gas-turbine units in construction. In addition to the regenerator, they also have a gas cooler at the exit which lowers the gas temperature to its initial level. In closed-cycle gas-turbine unit there is no combustion chamber. Instead, they have a heater (a furnace or a nuclear reactor) in which the working fluid (air, inert gases or their mixtures) do not mix with the combustion products of the fuel.
There are also combined units with gas and steam turbines—steam-gas units and gas-steam units—in which two working fluids, namely gas and steam, are used in one power-generating system. These units have better characteristics than modern steam-turbine systems and gas-turbine units. These combined gas and steam-turbine units make it possible to combine, in one thermal cycle, the high-temperature heat input (characteristic for gas-turbine units) and low-temperature (as in a steam-turbine unit condensor) heat removal. As a result, they provide conditions for obtaining high thermal efficiency of the cycle, thus high economy of energy generation. The efficiency of these combined units (steam-gas and gas-steam) may reach 50% at high values of the gas-turbine unit parameters; therefore, they are considered promising systems for power engineering. The high efficiency of turbine units with steam and gas turbines facilitate the solution of a very important problem of decreasing the amount of dangerous effluents with the aim of environmental protection.
The numerous combined turbine units in operation or under development differ by their heat schemes and the equipment used. They are classified mainly in accordance with the principle by which the fuel combustion heat is utilized.
If the main portion of heat is supplied with the fuel in the furnace of the boiler of the steam-turbine part these combined units are termed steam-gas units. If the main portion of heat is supplied with the fuel to the gas-turbine unit combustion chamber, these units are termed gas-steam units.
On the basis of the principle of interaction of working fluids, the combined systems are divided into two main groups: separate circuit units in which steam-water and gaseous working fluid move along separate paths and interact only across the heat exchanger surface, and contact-type units in which the combustion products mix with the steam-water working fluid prior to expansion in the gas-steam turbine.
Steam-gas units have separate circuits. There are steam-gas units of three types: those with a high head steam generator, those with a low head steam generator and those units using the waste heat of the gas turbine for heating the feed water in the steam-turbine unit. In the steam-gas units of the first type, the high head steam generator, is usually combined with the gas-turbine unit combustion chamber and the fuel burns at high pressure. In order to decrease the temperature of the waste gases, a gas-water heater is usually mounted downstream of the gas turbine. The heater partially replaces steam regeneration in the steam-turbine section of the unit. In steam-gas units with a low head steam generator, the waste gases from the gas-turbine unit pass into the furnace of a conventional boiler and are used for burning additional fuel, which may be not only liquid or gaseous but also solid, such as coal. There is also a gas-water heater downsteam of the low head steam generator. In such plants, the gas turbine unit is a sort of topping plant; this scheme is therefore used for reconstructing steam-turbine plants operating at lowered steam parameters. In the units of the third type, the exhaust gases from the gas-turbine unit are directed into the gaseous-feed water boiler where the heat of the exhaust gases is utilized. This heat may be sufficient to exclude regenerative feed water heaters. However, greater economic effect may be reached if the steam-gas system consists of multicomponent gas-turbine and steam-turbine units. In such a scheme, the condensate is heated in intermediate air coolers of the gas turbine unit and in the heater at the gas turbine unit exit. In order to create this type of combined system, it is not necessary to considerably change the boiler and the steam turbine regenerative system.
Gas-steam units may have either separate circuits or contact schemes. In gas-steam units with separate circuits, the fuel—or its main portion—is burnt in the gas-turbine unit combustion chamber. Sometimes the thermal cycle without fuel heat input to the steam-water working fluid is referred to as the binary gas-steam cycle. In some cases, a small amount of fuel (up to 15-20% of the total fuel flow rate of the gas circuit) is fed upsteam of the waste heat boiler. In the contact-type steam-gas units, water or steam is supplied to the high pressure circuit (downsteam of the compressor, into the combustion chamber or upsteam of the turbine). In gas-steam units with steam supply, a waste heat boiler is used for steam generation and utilizes a part of the turbine exhaust gases heat. This supply of water or steam increases the working fluid flow rate through the turbine as compared with the air flow rate through the compressor and thus increases its output. As the amount of power required for pumping the water is small, the capacity of the unit increases not less than 100 per cent. The disadvantage of the contact type gas-steam units is the requirement of chemical cleaning of the water which is exhausted with the gas.
One of the most promising designs is the steam-gas turbine which uses low calorific gas generated in the process of coal gasification as the gas-turbine unit fuel. The schemes of this type of units are essentially similar to the schemes of steam-gas units with high head steam generators and steam-gas units with low head steam generators. Their main structural difference is the inclusion of the gasification system with purification of the fuel gas generated of unburnt particles and sulfur.
Among other fields of application one should mention the application of driving stationary gas-turbine units in gas pipelines. Superchargers and gas-turbine units comprise the gas-pumping system. Some of these system were created on the basis of existing aircraft and marine gas-turbine engines.
Gas-turbine units for power generation are used mainly as peak-load units, that is the units operating 500-1500 hours per year during peak loads in the power system. The main advantages of gas-turbine units which make them applicable in power engineering are their higher manoevrability (the possibility of quick start and reliable operation under cyclic conditions) as compared with steam-turbine units, simplicity of automation, compactness, and independence of water sources.
Gas-turbine units which are elements of steam-gas units and gas-steam units use gaseous and liquid fuel and have unit capacity from 100 to 600 mW. These units are especially widely used in the USA.
About 10 per cent of all gas-turbine units produced in the world are used in different kinds of ships. The marine gas-turbine units may be competitive with Diesel engines as far as their main economic characteristics are concerned. Both steam-gas and gas-steam units may be used as marine propulsion units. Specific fuel consumption of existing marine gas-steam units of about 40 mW capacity is not larger than 240 g/(kW hr). Also in use are combined marine propulsion systems consisting of a gas-turbine engine and a Diesel engine which are not combined by a common thermodynamic cycle.
Automotive gas-turbine engines are considered as a good alternative to piston-type internal combustion engines. Their further progress is closely linked with the development of ceramic blades and disks.
Gas-turbine engines are widely used in aviation. Their monopoly is connected with their high specific power, thrust and high efficiency.
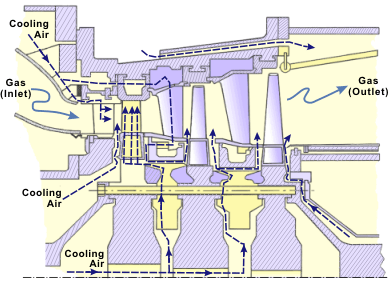
Gas turbines and gas-turbine units are characterized by a great variety of designs (depending on their application). However, with the exception of automotive gas-turbine engines, all of them have one common feature; as a rule, they all need cooling. The air bled from the compressor outlet is generally used as a cooling medium. Practically the whole turbine flow passage is air cooled (see Figure 4). The cooling should be intensive because the thermal resistance of metal alloys is limited and ceramic materials for turbine blades are still in the process of development.
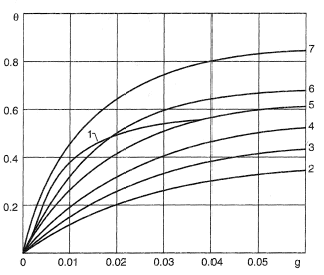
The general trend of research and development is to increase the turbine blade cooling efficiency which is determined by the depth of cooling θ = (Tg – Tw)/(Tg – Ta), where Tg is the temperature of the gas flowing over the blade, Ta is the coolant temperature and Tw is the temperature of the blade external surface. Dependences like those given in Figure 5 are used to evaluate the cooling efficiency (g is the relative cooling air flow rate, which is determined as the ratio of the flow rate of the air used for cooling to the flow rate of the air at the compressor inlet). The blade with a porous sheath has the highest cooling efficiency (curve, 7); the cooling efficiency of the blade with film cooling is somewhat lower. Blades with film cooling (curve, 6) have several hundreds of small diameter holes (0.4 to 0.6 mm) in the thin-walled sheath. Curves 1 through 5 illustrate the cooling efficiency of blades cooled using different methods of convective cooling.
Intensification of heat transfer in the internal passages of cooled blades and reduction of additional losses due to cooling may increase the efficiency of gas-turbine units with cooled turbines.
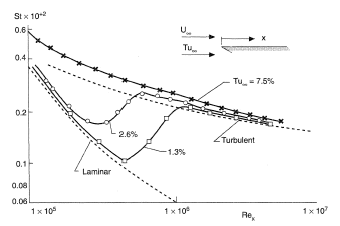
Thermal conditions of gas-turbine blades differ somewhat from those of stationary surfaces across which a gas flows. They are characterized by a high turbulence level of the incoming flow, by surface curvature, pressure gradient and body forces. Transition from laminar to turbulent flow in the boundary layer at the turbine blade surface is very important for determining heat transfer. There are factors which either accelerate this process or retard it.
Figure 6 presents experimental data for the dependence of the dimensionless heat flux (Stanton number St) on the Reynolds number Rex at the flat plate for various turbulence levels of the incoming flow Tu∞.
An increase of Tu∞ from 1.3 to 7.5% decrease the value of the Reynolds number at which turbulent flow is developed from 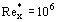 to
to  .
.
As compared with the flat plate case, the flow around the gas-turbine blade is characterized by a high level of flow acceleration over the suction surface. This high flow acceleration retards transition from laminar to turbulent flow, that is, its action is opposite to the incoming flow turbulence level.
To describe accelerated flows, the dimensionless acceleration parameter  is used where Re(l) is the unit Reynolds number Re(l) = Ue/νβ = (dUe/ds) is the gradient of velocity of the flow in the interblade channel and ν is the kinematic viscosity.
is used where Re(l) is the unit Reynolds number Re(l) = Ue/νβ = (dUe/ds) is the gradient of velocity of the flow in the interblade channel and ν is the kinematic viscosity.
The acceleration parameter K may be defined without solving the boundary layer equation on the basis of known distributions of the flow gas dynamic parameters in the interblade channel.
The analysis of results of temperature measurements on the rotating blades shows that the determining factor is not the incoming flow turbulence level Tu∞, but its local value Tue in a given interblade channel section. It may be assumed that
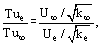
where ke is the local value of turbulent kinetic energy, k∞ is the same parameter in the incoming flow. Calculations show approximately 10 per cent decrease in ke in the area from the leading edge to the trailing edge of the turbine blade. This allows the determination of the local turbulence intensity using the following relationship for inviscid flow: Tue/Tu∞ = U∞/Ue.
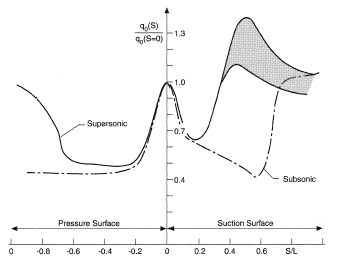
Figure 7 presents the comparison of the heat flux q0 distribution along the same profile for supersonic and subsonic flows. The variation of the heat flux along the relative coordinate S/L is complex and nonmonotonic. From the analysis of the results obtained it follows that intensive turbulent pulsation of the flow around a supersonic blade accelerates transition to turbulent flow in the boundary layer at the blade surface. In the case of a subsonic blade, especially at the suction surface, this transition is retarded, which results in a considerable difference in the heat transfer level.
Suppression of turbulence in the boundary layer is observed only in the case where the acceleration parameter K is higher than 3 × 10−6 . If the free stream turbulence is not high, even relaminarization of already developed turbulent boundary layer is possible.
REFERENCES
Horlock, J. H. (1966) Axial Flow Turbines, Butterworths, London, 1966.
Kostyuk, A. and Frolov, V. (1988) Steam and Gas Turbines, Moscow, Mir. Heat Transfer and Fluid Flow in Rotating Machinery, (1987).
Wen-jei Yang, Ed., Washington etc., Hemisphere.
References
- Horlock, J. H. (1966) Axial Flow Turbines, Butterworths, London, 1966.
- Kostyuk, A. and Frolov, V. (1988) Steam and Gas Turbines, Moscow, Mir. Heat Transfer and Fluid Flow in Rotating Machinery, (1987).
- Wen-jei Yang, Ed., Washington etc., Hemisphere.