The term flashing flow is reserved for the flow with dramatic evaporation of liquid due to a drop of pressure P. The process of production of the vapor phase is usually accompanied by massive thermodynamic and mechanical nonequilibrium by virtue of a difference in temperature and velocity of both phases. The rate of evaporation in a fluid volume during the flashing flow changes according to two factors the number of nuclei and the superheat of liquid. Thermodynamic nonequilibrium, which plays the most important role in the flashing flow reflects the necessity of liquid being superheated above its saturation temperature Ts(P), to encourage the production of vapor bubbles. The vapor phase can be created on nuclei like particles of a gas dissolved in the liquid or solid particles. With the emergence of vapor bubbles on these nuclei, there begins a process of heterogeneous flashing. In the case of pure and gas-free liquid, the vapor phase can be produced at the occurrence of fluctuations of density in the liquid due to temperature fluctuations. That type of flashing is referred to as homogeneous flashing and takes superheating of dozen or several dozen of degrees. The initial difference between temperature of the liquid T1, and temperature of the vapor Tv, namely ΔT = T1 – Tv > 0, is a driving force of the growth of vapor bubbles and thus for the increase in void fraction.
Several stages of the Bubble Growth can be distinguished. In the first early stage, as the vapor bubble is small, the inertia force of the liquid surrounding the bubble has to be taken into account and the Rayleigh-Lamb equation is appropriate. The second stage is called the thermal stage when bubble growth is determined entirely by the heat flux from the liquid to the vapor due to the superheat ΔT

where α is the heat transfer coefficient referring to the transfer of heat from the superheated liquid to the interfacial area (e.g., to the vapor bubble in the early stage of the flashing flow). In practical applications, when surface tension is neglected, it can be assumed that the entire heat flux from the superheated liquid to the interfacial area is used for the production of the mass flux of the vapor phase per unit of the volume

where x denotes the dryness fraction, ρ density of the two-phase mixture being produced and hfg the heat of evaporation. For the two-phase flow through a channel, the dryness fraction can be averaged across the channel, being a function of the distance z from the origin of the coordinate system and of time t. In the case of flashing flow, the dryness fraction x has a lower value than the dryness fraction x referred to the equivalent equilibrium state. The latter is determined by means of two thermodynamic parameters, e.g., pressure P and enthalpy h.

where h'(P) is enthalpy of saturated liquid corresponding to the line of
 .
.
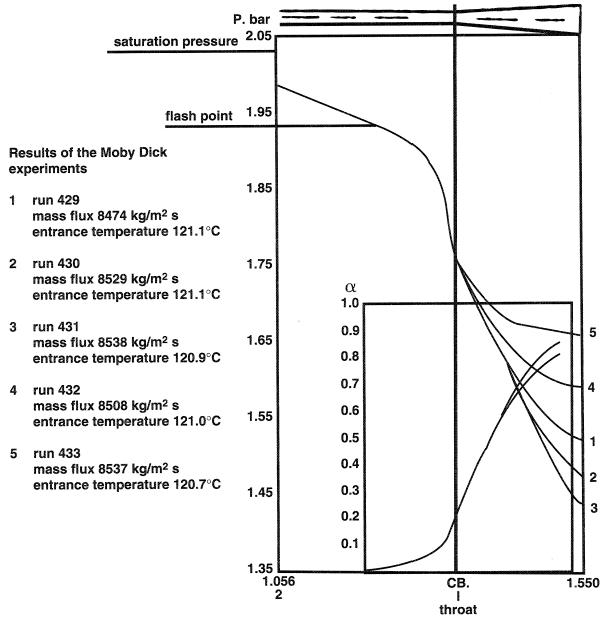
Flashing flow was investigated in detail on the basis of the well-documented Moby Dick experiments described by Réocreux1 and Bouré et al.2 The Moby Dick experiments were carried out in a channel consisting of a straight portion followed by a conical expander provided with a 7° included-angle divergence. Measurements of pressure and void fraction, as functions of longitudinal distance, were reported. A typical pressure profile is shown in Figure 1 which represents runs at the same upstream conditions and mass-flow rate, but at different back pressures. The diagram also plots the variation of the void fraction, measured by beta-ray absorption.
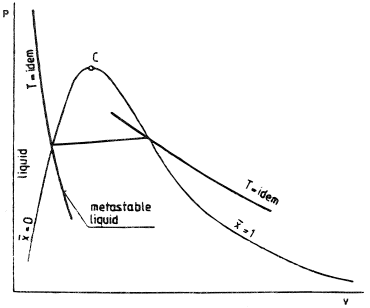
A distinct feature of flashing flow is that the liquid is in a metastable region, that is, at temperature T1 higher than the saturation temperature Ts(P); T1 > Ts. The transition which the liquid undergoes during flashing flow with a pressure drop bears much resemblance to the isothermal transition as shown in Figure 2. Heterogeneous flashing in a channel can be initiated at a superheat of 2-3°C like that found in the Moby Dick experiments. Practically, it can be established that in the early stage, when the flashing flow starts becoming bubbly in structure, the temperature of the vapor is equal to its saturation temperature.
A theoretical description of flashing flow based on the one-dimensional relaxation model3 was proposed by Bilicki et al.4 The assumption was made that the flow turns into two-phase at a state where the liquid becomes superheated by ΔT. The value of superheat at the flashing point was determined from experiments and ranged from 2.66 to 2.91°C. So far, no theory exists which would make it possible to determine ΔT for heterogeneous nucleation, although such a possibility was considered, among others, in Skripov et al.5 The above mentioned mathematical model of flashing flow draws on the set of one-dimensional equations of conservation of mass, momentum and energy:




where w denotes the barycentric velocity of the two-phase mixture, τ is the shear stress given by a closure equation, C the circumference of the channel, A its cross-section area. The above set of equations is supplemented with the rate equation which describes nonequilibrium state

where θx is the relaxation time, x denotes the actual dryness fraction as different from its equilibrium value. The state equation must also be added

where v is the specific volume of the two-phase mixture during the flashing flow, h1 enthalpy of the liquid in the metastable region.
The presented model of flashing flow assumes knowledge of the relaxation time and superheat at the flashing point. Both quantities should be determined from experiments as we do not have at our disposal any method for their theoretical determination. In Figure 3 there is presented a comparison of pressure profiles obtained theoretically and from the Moby Dick experiments.

Figure 3. Experimental results for run 401 of the Moby Dick experiments1 and theoretical predictions3.
A different model of flashing flow was recently proposed by Riznio and Ishii.6 This model relies on the wall nucleation theory, bubble growth model and drift flux transport model.
In the preceding years flashing flow was linkend with critical flow.6 The papers of7-13 illustrate the variety of approaches to this problem.
REFERENCES
1. Réocreux, M. L. (1974) Contribution a 1'étude des debits critiques en écoulement diphasique eau-vapeur. Ph.D. thesis. Université Scientifique et Medicale de Grenoble.
2. Bouré, J. A., Fritte, A. A., Giot, M. M. and Réocreux, M. L. (1976) Highlights on two-phase critical flow. Int. J. Multiphase Flow, 3, 1-22. DOI: 10.1016/0301-9322(76)90030-6
3. Bilicki, Z., Kestin, J., and Pratt, M. M. (1990) A reinterpretation of the Moby Dick experiments in terms of nonequilibrium model. J. Fluids Engineering, Trans. ASME, 112, 112-117.
4. Bilicki, Z. and Kestin, J. (1990) Physical aspects of the relaxation model in two-phase flow, Proc. Royal Soc., Lond. A, 428, 379-397.
5. Skripov, V. P., Sinitsyn, E. N., Pavlov, P. A., Ermakov, G. V., Muratov, G. N., Bulanov, N. V. and Baidakov, V. G. (1988) Thermophysical Properties of Liquids in the Metastable (Superheated) State. Gordon and Breach Science Publishers New York, London.
6. Riznic, J. R. and Ishii, M. (1989) Bubble number density and vapor generation in flashing flow. Int. J. Heat Mass Trans. 32, 1821-1833. DOI: 10.1016/0017-9310(89)90154-3
7. Ardron, K. H. and Furness, R. A. (1976) A study of the critical flow models used in reactor blowdown analysis. Nucl. Eng. Des. 39, 257-266. DOI: 10.1016/0029-5493(76)90074-1
8. Jones, Jr. O. C. and Saha, P. (1977) Non-equilibrium aspects of water reactor safety, Proc. Symp. on the Thermal and Hydraulic Aspects of Nucl. Reactor Safety, Vol. 1 Liquid Water Reactors (Edited by O. C. Jones, Jr. & S. G. Bankoff). ASME, New York.
9. Weismann, J. and Tentner, A. (1978) Models for estimation of critical flow in two-phase systems. Prog. Nucl. Energy, 2, 183-197. DOI: 10.1016/0149-1970(78)90007-0
10. Abdollahian, D. Healzer, J. and Janseen, E. (1980) Critical Flow Data Review and Analysis. Part I—Literature Survey, SLI-7908-1, revised 11/80, November.
11. Jones, Jr. O. C. (1979) Flashing inception in flowing liquids, Non-equilibrium Two-phase Flow (Edited by J. C. Chen and S. G. Bankoff), 29-34. ASME, New York.
12. Shin, T. S. and Jones, O. C. (1993) Nucleation and flashing in nozzles-1. A distributed model. Int. J. Multiphase Flow, 19, 943-964. DOI: 10.1016/0301-9322(93)90071-2
13. Blinkov, V. N., Jones, O. C. and Nigmatulin, B. I. (1993) Nucleation and flashing in nozzles-2. Comparison with experiments using a five-equation model for vapor void development. Int. J. Multiphase Flow, 19,965-986. DOI: 10.1016/0301-9322(93)90072-3
References
- Réocreux, M. L. (1974) Contribution a 1'étude des debits critiques en écoulement diphasique eau-vapeur. Ph.D. thesis. Université Scientifique et Medicale de Grenoble.
- Bouré, J. A., Fritte, A. A., Giot, M. M. and Réocreux, M. L. (1976) Highlights on two-phase critical flow. Int. J. Multiphase Flow, 3, 1-22. DOI: 10.1016/0301-9322(76)90030-6
- Bilicki, Z., Kestin, J., and Pratt, M. M. (1990) A reinterpretation of the Moby Dick experiments in terms of nonequilibrium model. J. Fluids Engineering, Trans. ASME, 112, 112-117. DOI: 10.1115/1.2909390
- Bilicki, Z. and Kestin, J. (1990) Physical aspects of the relaxation model in two-phase flow, Proc. Royal Soc., Lond. A, 428, 379-397.
- Skripov, V. P., Sinitsyn, E. N., Pavlov, P. A., Ermakov, G. V., Muratov, G. N., Bulanov, N. V. and Baidakov, V. G. (1988) Thermophysical Properties of Liquids in the Metastable (Superheated) State. Gordon and Breach Science Publishers New York, London.
- Riznic, J. R. and Ishii, M. (1989) Bubble number density and vapor generation in flashing flow. Int. J. Heat Mass Trans. 32, 1821-1833. DOI: 10.1016/0017-9310(89)90154-3
- Ardron, K. H. and Furness, R. A. (1976) A study of the critical flow models used in reactor blowdown analysis. Nucl. Eng. Des. 39, 257-266. DOI: 10.1016/0029-5493(76)90074-1
- Jones, Jr. O. C. and Saha, P. (1977) Non-equilibrium aspects of water reactor safety, Proc. Symp. on the Thermal and Hydraulic Aspects of Nucl. Reactor Safety, Vol. 1 Liquid Water Reactors (Edited by O. C. Jones, Jr. & S. G. Bankoff). ASME, New York.
- Weismann, J. and Tentner, A. (1978) Models for estimation of critical flow in two-phase systems. Prog. Nucl. Energy, 2, 183-197. DOI: 10.1016/0149-1970(78)90007-0
- Abdollahian, D. Healzer, J. and Janseen, E. (1980) Critical Flow Data Review and Analysis. Part I—Literature Survey, SLI-7908-1, revised 11/80, November.
- Jones, Jr. O. C. (1979) Flashing inception in flowing liquids, Non-equilibrium Two-phase Flow (Edited by J. C. Chen and S. G. Bankoff), 29-34. ASME, New York.
- Shin, T. S. and Jones, O. C. (1993) Nucleation and flashing in nozzles-1. A distributed model. Int. J. Multiphase Flow, 19, 943-964. DOI: 10.1016/0301-9322(93)90071-2
- Blinkov, V. N., Jones, O. C. and Nigmatulin, B. I. (1993) Nucleation and flashing in nozzles-2. Comparison with experiments using a five-equation model for vapor void development. Int. J. Multiphase Flow, 19,965-986. DOI: 10.1016/0301-9322(93)90072-3