Thermal conduction is the transfer of heat from hotter to cooler parts of a body resulting in equalizing of temperature. In contrast to heat transfer by convection, thermal conduction has nothing to do with macroscopic displacements in the body, but is a result of a direct energy transfer between particles, such as molecules, atoms, and electrons, with higher energy and ones with lower energy. Contrary to heat transfer by radiation, there is no thermal conduction in vacuum.
The basic law of thermal conduction is the Fourier law which states that the heat flux density
 is proportional to the temperature gradient T in an isotropic body:
is proportional to the temperature gradient T in an isotropic body:
 =−λgradT. The constant of proportionally λ is the thermal conductivity. The minus sign indicates that the temperature decreases in the direction of heat transport and, hence, the temperature gradient is a negative quantity.
=−λgradT. The constant of proportionally λ is the thermal conductivity. The minus sign indicates that the temperature decreases in the direction of heat transport and, hence, the temperature gradient is a negative quantity.
Deviations from the Fourier law can be observed at extremely high values of gradT, e.g., in powerful shock waves, at low temperatures for liquid helium HeII, and at high temperatures on the order of tens of thousands of degrees when energy transfer in gases is due mainly to radiation. In highly rarefied media, in which molecules collide with the walls of the vessel rather than with one another, the concept of local temperature is meaningless and the Fourier law is inapplicable. In this case, we deal not with thermal conduction in a gas, but with heat exchange between the bodies in it.
Among solid, anisotropic substances (e.g., crystals, sedimentary rocks, lamellar and pyrolytic materials) occur for which the heat flux density vector
 does not coincide with the normal to an isothermal surface. The simplest assumption generalizing the Fourier hypothesis is that each component of the vector
does not coincide with the normal to an isothermal surface. The simplest assumption generalizing the Fourier hypothesis is that each component of the vector
 at the point (x, y, z) is a linear combination of all the components of the temperature gradient in it
at the point (x, y, z) is a linear combination of all the components of the temperature gradient in it

the coefficients of thermal conductivity λik of anisotropic body form a tensor in the 2nd dimension. For crystals, it is found, within the measurement error, that thermal conductivity in mutually opposite directions is the same.
In multicomponent gas mixtures, one has to take into account the so-called "cross effects" such as mass flows brought about by the temperature gradient (thermal diffusion or the Soret effect), energy flows due to density gradient (diffusion thermal effect or the Dufour effect). The heat flux density in a n-component gas mixture is written down as a sum

where n and ni are the total number of molecules and the number of molecules of a given species per unit volume, hi and mi the enthalpy and the mass of a single particle of the ith species,
 the diffusion rate, Dij the coefficient of binary diffusion,
the diffusion rate, Dij the coefficient of binary diffusion,
 the coefficient of thermal diffusion (Dufour effect), and K is Boltzmann’s constant. Thus, in multicomponent gas mixtures energy transfer is also accomplished, in addition to convection and heat conduction, by diffusion flow of molecules relative to the bulk velocity and by the Dufour effect. In this case the apparent thermal conductivity may be far different from the molecular thermal conductivity λ.
the coefficient of thermal diffusion (Dufour effect), and K is Boltzmann’s constant. Thus, in multicomponent gas mixtures energy transfer is also accomplished, in addition to convection and heat conduction, by diffusion flow of molecules relative to the bulk velocity and by the Dufour effect. In this case the apparent thermal conductivity may be far different from the molecular thermal conductivity λ.
If we assume that the coefficient of thermal conductivity λ as well as the coefficient of heat capacity c and the density ρ of a substance do not depend on other parameters, then in the absence of internal heat sources the temperature inside the body is described by the differential equation of thermal conductivity

where
 is the Laplacian, τ the time, and x, y, z the Cartesian coordinates.
is the Laplacian, τ the time, and x, y, z the Cartesian coordinates.
The group k = (λ/ρc) is known as thermal diffusivity. It characterizes the velocity of propagation of isothermal surfaces in a body.
Solving equations of thermal conduction enables the establishment of the temperature distribution T(τ, x, y, z) to a certain degree of accuracy for any body. The degree of accuracy depends on the initial and boundary conditions. Solution of the equation of thermal conductance in a general form, including the variable coefficients λ, c, and ρ, using high-speed computers, in principle presents no difficulties. But this specifies higher requirements for reliability in determining the varable coefficient of thermal conductivity λ for the given substances. Numerous theoretical and experimental investigations have led to the discovery of some specific features and regularities.
The highest thermal conductivity is inherent in metals (see Table 1). Amongst the metals silver shows the highest thermal conductivity and bismuth the lowest. In the temperature range above ambient, λ for nearly all pure metals falls with increasing temperature. λ is greatly affected by the presence of additives and impurities. Thus, the coefficient of thermal conductivity for steel containing 1% carbon is 40% lower than for pure iron. For metals it depends to a great extent on their treatment. Quenching and cold treatment of metals decrease λ, while preheating up to a high temperature increases it.
Table 1. The values of the coefficient of thermal conductivity for various substances at atmospheric pressure and moderate temperatures

Thermal conductivity of nonmetallic liquids under normal conditions is much lower than that of metals and ranges from 0.1 to 0.6 W/mK. In the interval between the melting point and the boiling point, thermal conductivity of liquids may change by a factor of 1.1 to 1.6.
Finally, the lowest thermal conductivity is observed in gases (under normal conditions it is from 0.006 to 0.1 W/mK). Hydrogen and helium are distinguished among gases for the highest thermal conductivity.
The coefficients of thermal conductivity presented in the table evidence that this parameter varies widely. It is determined using various techniques based on the molecular kinetic theory, the phenomenological approaches of the generalized conductivity theory, and generalization of experimental data. Below the investigation results are presented for the different classes of substances.
Thermal conductivity in gases is brought about by energy transfer by gas molecules in the same way as viscosity is related with momentum transfer and diffusion, with mass transfer. Therefore, all these phenomena appreciably depend on
 , that is the mean free path of molecules.
, that is the mean free path of molecules.
For the model of gas consisting of solid spherical molecules which do not interact at a distance and possess only the energy of translational motion, the coefficient of thermal conductivity X is determined by the kinetic theory of gases as λ =
 , where ρ is the gas density, cv the heat capacity of unit of mass at constant volume, and
, where ρ is the gas density, cv the heat capacity of unit of mass at constant volume, and
 the arithmetical mean velocity of the molecules. The viscosity coefficient η for this gas is equal to
the arithmetical mean velocity of the molecules. The viscosity coefficient η for this gas is equal to
 . Because of a highly simplified gas model underlying the calculation of λ and η, we cannot expect a fair agreement of theory and experiment. For instance, these are departures from the theoretical deduction of independence of λ and p since there are deviations from the relationships ρ
. Because of a highly simplified gas model underlying the calculation of λ and η, we cannot expect a fair agreement of theory and experiment. For instance, these are departures from the theoretical deduction of independence of λ and p since there are deviations from the relationships ρ
 p and
p and

 1/p. However, the relation between the coefficients of transfer λ = ηcv observed theoretically is quite correct.
1/p. However, the relation between the coefficients of transfer λ = ηcv observed theoretically is quite correct.
Contemporary kinetic theory takes into account the existence of the attraction and repulsion forces between molecules. Expression for these forces can in principle be derived from quantum mechanics although this is a laborious task if all atoms and molecules are considered, except in the simplest ones. Therefore, the molecular interaction is described, as a rate, by simple empirical functions, that is interaction potentials containing variable parameters.
The Lennard- Jones potential

is used as a function for gases and gas mixtures at moderate temperatures, where ε is the depth of the potential pit, σ the effective diameter of the molecule or the radius r for which φ = 0. Selection of interaction potentials allows us to construct theoretical models, which quite adequately approximate experimental data for nonatomic gases over the entire temperature range, except for the very lowest temperatures, where light gases exhibit quantum effects.
Internal degrees of freedom of polyatomic molecules are commonly taken into account using the Euken correction λ = η(2.5ct + cr), where ct is the heat capacity due to translational motion of molecules alone and cr the heat capacity due to the energy of rotational, and vibrational degrees of freedom and due to electron energy. Considering that cv = ct + cr and ct =
 where R is the universal gas constant and
where R is the universal gas constant and
 the molecule mass, we can write
the molecule mass, we can write

where cp is the heat capacity at a constant pressure. The minimum and the maximum Euken corrections are 1/19 and 2.5, respectively.
Euken's relation can be explained theoretically if we assume that energy exchange between translational and the remaining degrees of freedom takes little time, i.e., the relaxation time is short. Euken's hypothesis better agrees with reality at high temperatures when the number of collisions per second is great.
Many efforts have been made to attain a better consistency with experimental data for polyatomic gases by a further complication of the model of energy exchange between degrees of freedom. Thus, Mason and Monchick discussed another limit case when the time of relaxation is long. Taking into account this fact leads to a smaller contribution of translational and a larger contribution of rotational degrees of freedom to thermal conductivity.
The molecular kinetic theory takes account only of pairwise molecule collisions, therefore, it is not applicable at high gas densities when ternary collisions come into play. The experimental data demonstrate that, as pressure rises, the coefficient of thermal conductivity grows for all the gases. It has been established that at low and medium pressures (up to a few bars) the increase in λ with increasing p is relatively small and is no higher than 1% of the coefficient of thermal conductivity per bar.
Thermal conductivity of gas mixtures generally is not a linear function of the mixture composition and can be higher or lower than the ones for the original component. Methods based on molecular kinetic concepts and those based on phenomenological concepts have been developed. Thus, a gas mixture is sometimes represented as a hypothetical quasi-homogeneous gas the molecule size of which is determined as a mean arithmetical sum taken over effective diameters of components, σ = 1/2 (σ1 + σ2) and the depth of the potential pit is related to similar parameters of components as
 . The reduced mass of molecules of a quasi-homogeneous gas is determined by the relation
. The reduced mass of molecules of a quasi-homogeneous gas is determined by the relation
 .
.
There exist a great vanity of correction factors taking account of nonsymmetric molecule shape, incomplete momentum and energy exchange during the time of a single collision, and different types of interaction potentials (Mason, Saxena, et al.).
For mixtures of nonpolar gases, Brocaw suggested an easy rule supported in practice, λm = 1/2 (λsm + λrm), where λsm and λrm are respectively thermal conductivities of structures formed by alternating plane layers, arranged parallel and perpendicular to the heat flux direction


Here x1, x2, ... are the molar fractions of the components.
For gas mixtures containing polar molecules or for high pressure mixtures Brocaw's formula has to be replaced by a more intricate expression.
Most theoretical and semiempirical expressions for the coefficient of thermal conductivity in liquids are based on the model, suggested by Bridgman, which recognizes that the sound velocity Us in a liquid exceeds by 5- to 10-fold velocity of motion of the molecules determined from the kinetic theory. Another distinction from gases consists in the fact that in the relation for the coefficient for thermal conductivity, instead of heat capacity at a constant volume cv, the heat capacity at a constant pressure cp is taken
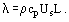
Here L is the mean intermolecular spacing, L = Δ – d and Δ the center-to-center distance of molecules of diameter d.
The coefficient of thermal conductivity λ calculated by the above formula substantially differs from the value calculated by the molecular kinetic theory of gases. However, the consistency of calculation results and experimental data is also not good enough, commonly the difference is from 5% to 15%, but sometimes it amounts to 50%.
The coefficients of thermal conductivity and viscosity of liquids obey more intricate laws than these for gases. In particular, no simple proportionality characteristic of gases exists between λ and μ. As a rule, λ and μ for liquids diminish with temperature, nevertheless the effect of temperature on λ is far weaker than on μ.
Such an extraordinary behavior is accounted for by the fact that, in contrast to gases, interaction of intermolecular force fields in liquids prevents any relative motion of neighboring layers. With increasing T the energy of thermal motion loosens the molecules decreasing the attraction forces and, hence, the coefficients of viscosity η and of thermal conductivity λ decrease. The function λ(T) can be approximated by a linear dependence with the proportionality factor from −0.0005 to –0.002 for different types of liquids.
Since the velocity of sound for many liquids is uncertain, semiempirical relations based on more certain physical characteristics received recognition. Thus, Missenard suggested the formula λ =
 , where B can be considered a constant for all the liquids with the same number of atoms in the molecule N (B is approximately proportional to N−0.25) and Ts is the boiling point of the liquid.
, where B can be considered a constant for all the liquids with the same number of atoms in the molecule N (B is approximately proportional to N−0.25) and Ts is the boiling point of the liquid.
For all liquids the coefficient of thermal conductivity increases with increasing pressure. Upon compression molecules draw together, their mutual attraction grows, therefore, viscosity and thermal conductivity increase. However, up to pressures of the order of 50 bars, λ increases only slightly and the variation can be neglected. At high pressures (p = 12000 bars) thermal conductivity of water grows by less than 50% and that of n-pentane, by no more than 70%.
Contrary to gas mixtures in which components are mixed at the atomic and molecular level, the structure of systems with liquid components can differ essentially, viz., from ideal solutions to emulsions in which aggregations of homogeneous components may be higher than 109 units and more. But reliable and systematized data are still scarce.
Based on generalized experimental data Filippov suggested an empirical relation for estimating thermal conductivity of solutions

where C1 and C2 are the mass concentrations of components with thermal conductivities λ1 and λ2 respectively.
To calculate thermal conductivity of electrolytes (salt solutions), Missenard recommends the expression

where
 , N, ρ, and Tm are the molecular mass of the molecules, the number of atoms in a molecule, the electrolyte density, and the melting point, respectively.
, N, ρ, and Tm are the molecular mass of the molecules, the number of atoms in a molecule, the electrolyte density, and the melting point, respectively.
Thermal conductivity of solids is of a different nature depending on whether or not they are conductors. In dielectrics with no free electrical charges, thermal energy is transferred by phonons. The collective vibrations of atoms in crystal lattice take the form of displacement waves, the interference of which generates wave packets, i.e., phonons. The displacement waves bring about fluctuations of density that can be manifested as a variation of refractive index. If the waves pass through a region in which the refractive index differs from the mean volumetric value, the subsequent displacement waves carrying the energy of thermal motion will be scattered.
The scattering is the stronger, the more the maximum deviation of atoms from their mean positions in the lattice, i.e., the higher the T. This accounts for the experimentally established fact that thermal conductivity of crystal dielectrics decreases at fairly high temperatures: λ
 1/T (Figure 1).
1/T (Figure 1).
Debye gave an insight into a peaklike character of λ(T) variation at low T within the framework of quantum mechanical concepts. He elaborated a dipole theory of dielectrics based on the concept of a molecule as a rigid dipole. In this model Debye introduced the concept of the so-called Debye temperature θD proportional to the maximum frequency of atomic vibrations in a solid. For most substances θD is either lower than or close to the room temperature (an exception is diamond for which θD = 1850 K and berrylium for which θD = 1160K).
In the quantum theory of solids, the crystal lattice is considered as a volume filled with phonon gas to which the deduction of the simplest kinetic theory is applied

where c is the heat capacity of a dielectric that coincides with that of phonon gas, v the mean velocity of phonons approximately equal to the sound velocity,
 the mean free path of phonons. The existence of a certain finite value of
the mean free path of phonons. The existence of a certain finite value of
 is the result of phonon scattering on phonons, on defects of crystal lattice and, in particular, on grain boundaries over the entire specimen. The temperature dependence λ(T) is determined by that of
is the result of phonon scattering on phonons, on defects of crystal lattice and, in particular, on grain boundaries over the entire specimen. The temperature dependence λ(T) is determined by that of
 and c on temperature.
and c on temperature.
At high temperatures substantially exceeding the Debye temperature θD, the basic mechanism limiting
 is a phonon-phonon scattering due to anharmonicity of atom vibrations in a crystal. The phonon-phonon mechanism of thermal resistance ((1/λ) is known as the coefficient of thermal resistance) is feasible only owing to a transition resulting in retardation of phonon flow and appreciable changing of quasi-momentum. The higher the T, the higher the probability of the transition with
is a phonon-phonon scattering due to anharmonicity of atom vibrations in a crystal. The phonon-phonon mechanism of thermal resistance ((1/λ) is known as the coefficient of thermal resistance) is feasible only owing to a transition resulting in retardation of phonon flow and appreciable changing of quasi-momentum. The higher the T, the higher the probability of the transition with
 decreasing:
decreasing:

 (1/T). Since at T > θD heat capacity c only slightly increases with temperature, hence, λ
(1/T). Since at T > θD heat capacity c only slightly increases with temperature, hence, λ
 1/T.
1/T.
At temperatures lower than the Debye temperature, T<<θD, the length of the mean free path
 determined by the phonon-phonon scattering grows drastically,
determined by the phonon-phonon scattering grows drastically,
 expθD/T and, as rule, is confined to the size of a crystal R. According to the Debye law heat capacity c in this temperature range varies as c
expθD/T and, as rule, is confined to the size of a crystal R. According to the Debye law heat capacity c in this temperature range varies as c
 (T/θD)3. Consequently, at T → 0 the coefficient of thermal conductivity λ must decrease in proportion to T3. The temperature for which thermal conductivity has a peak is determined from
(T/θD)3. Consequently, at T → 0 the coefficient of thermal conductivity λ must decrease in proportion to T3. The temperature for which thermal conductivity has a peak is determined from
 ≈ R, which commonly corresponds to T ≤ 0.05θD.
≈ R, which commonly corresponds to T ≤ 0.05θD.
This theory also accounts for the behavior of the coefficient of thermal conductivity for amorphous substances having no long-range order, i.e., the size of their "crystals" is of the order of atomic sizes. By virtue of this, scattering at the "boundaries" of these substances must prevail at all T and
 ≈ const. The coefficient of thermal conductivity of amorphous substances λ
≈ const. The coefficient of thermal conductivity of amorphous substances λ
 T3 at low temperatures and must grow slightly, in proportion to heat capacity, at moderate and high temperatures, T > θD.
T3 at low temperatures and must grow slightly, in proportion to heat capacity, at moderate and high temperatures, T > θD.
All this provides a qualitative explanation of the dependence λ(T) in real crystal dielectrics, but takes no account of deviations from the constant lattice due to atomic impurities of other elements and their own isotopes. At a high temperature the resistance which is offered by impurities to heat transport is independent of temperature. This makes it possible to estimate the degree of crystal purity from variation of its thermal conductivity with temperature. The same fact enables us to determine the distribution between glassy and crystal substance in the natural mineral if the glass is considered as an impurity in a crystal.
Thermal conductivity in metals depends on the motion and interaction of current carriers, i.e., conduction electrons. Generally, the coefficient of thermal conductivity λ of a metal equals the sum of lattice (phonon) λph, and electron λe components, λ = λe + λph; at ordinary temperatures, as a rule, λe >>λph.
If we apply a simple kinetic theory of gases to the flow of free electrons and assume that the length of their free path does not depend on velocity, then the theory implies that

where e is the electron charge, K Boltzrnann's constant, and σ the electrical conductivity. A strict quantum mechanical theory offers a similar relation,

In both formulas the ratio of the electron part of the coefficient of thermal conductivity λ to electrical conductivity σ, in a wide temperature range, appears to be in proportion to the temperature according to the Wiedemann-Franz law, λ/σ = LT, where L is the Lorentz number. This law is used to calculate λe from the measured electrical conductivity. However, it is violated at temperatures below θD when an electron-phonon interaction prevails (σ grows with decreasing T as T−5 while le varies more slightly as T−2).
The experimental findings evidence that, as a rule, thermal conductivity of metals at high temperatures is a slightly decreasing function of temperature. But there are many exceptions. Thus, thermal conductivity of iron strongly decreases with temperature while tantalum and niobium show a positive temperature coefficient.
Of interest are the attempts to compare the coefficients of thermal conductivity for different substances for a single characteristic temperature, for instance, for the melting point Tm of solids. Thus, the statistical processing of experimental data carried out by Missenard has shown that thermal conductivity of metals at the melting point λ(T = Tm) = λm is in proportion to λ

 and thermal conductivity of dielectrical crystals at T = Tm is in proportion to
and thermal conductivity of dielectrical crystals at T = Tm is in proportion to
 , where m is the molecular mass, N the number of atoms in the chemical formula, ρ the density, and the melting point Tm is in Kelvins.
, where m is the molecular mass, N the number of atoms in the chemical formula, ρ the density, and the melting point Tm is in Kelvins.
Heat transport in semiconductors is more complex than in dielectrics and metals because the phonon and the electron components are equally essential for them. Another reason for the complexity is the considerable effect of impurities, bipolar diffusion, and other little studied factors on heat transfer.
The effect of pressure on thermal conductivity of solids can be assumed, with a good accuracy, to be linear, λ for many metals growing with p.
For the effect of porosity on thermal conductivity of solids see Porous Medium.
REFERENCES
Wakeham, W. A., Nagashima, A. and Sengers, J. V. (1991) (Eds.), Experimental Thermodynamics, Vol. III, Chapters 6, 7 and 8, Blackwell Scientific Publications, Oxford.
Millat, J., Dymond, J. H. and Nieto de Castro, C. A. (1996) (Eds.), Transport Properties of Fluids: Their Correlation, Prediction and Estimation, Cambridge University Press, New York.
References
- Wakeham, W. A., Nagashima, A. and Sengers, J. V. (1991) (Eds.), Experimental Thermodynamics, Vol. III, Chapters 6, 7 and 8, Blackwell Scientific Publications, Oxford.
- Millat, J., Dymond, J. H. and Nieto de Castro, C. A. (1996) (Eds.), Transport Properties of Fluids: Their Correlation, Prediction and Estimation, Cambridge University Press, New York.
