RADIATIVE TRANSFER IN TURBULENT FLAMES
Following from: Radiative transfer in combustion systems; Combustion phenomena affected by radiation; Radiative transfer in laminar flames
Leading to: Radiative transfer in combustion chambers; Radiative transfer in two-phase combustion; Thermal radiation in unwanted fires
In spite of the fact that turbulent flames are commonly encountered in practical combustion systems, the effects of radiative transfer on the flame structure have been neglected in fundamental turbulent diffusion or premixed flame modeling studies (Borghi, 1988; Bilger, 2000). Many excellent textbooks on the fundamentals of combustion are available (Williams, 1985; Glassman, 1996; Turns, 2000), but they provide little discussion, if any, on turbulence and/or radiation coupling in flames and practical combustion systems. Practical needs have motivated many studies on turbulent flame radiation, and a comprehensive account of earlier fundamental studies on small laboratory flames is available (Faeth et al., 1989). In small-scale studies, the past research efforts include, but are not limited to, scalar flame structure, generation of pollutants in nonluminous and luminous flames, prediction of radiative transfer characteristics given the instantaneous or time-averaged scalar structure, and turbulence-radiation interaction (TRI). Requirements for the modern design of industrial combustion systems are efficient combustion, minimization of nitrogen oxide and particulate emissions, optimization of heat transfer, and thermal performance. These and other requirements are being addressed in current CFD codes (Baukal et al., 2001).
Global Radiation from Turbulent Flames
As discussed in Radiative transfer in laminar flames, loss of radiant energy from a flame has a number of consequences including the lowering of the flame temperature and thereby affecting the flame structure, NOx emissions, combustion characteristics, etc. One of the simplest ways of assessing the relative importance of radiation (global) on combustion is to determine (measure) the radiant fraction χr, which represents the ratio of radiant energy lost (radiated) from a free flame to the surroundings Qr to the rate of heat released by the combustion process in the flame Qc,

|
(1) |
where mF is the mass flow rate of the fuel and ΔHc is the heat of combustion of the fuel.
Radiant fractions have been measured for different fuels, and a discussion is available (Viskanta, 2005). For example, the radiant fractions have been measured for a number of different fuels and various-size burners. The maximum radiant fractions for C2H2, C3H8, and CH4 are about 0.6, 0.45, and 0.15, respectively. These values should depend strongly on the optical paths and flame scales. The fractions for the same burner size are lower for methane (CH4) and larger for ethylene (C2H2) than for propane (C3H8) flames. This is because C2H2 has a greater propensity for soot formation than C3H8 and CH4. For a given burner diameter, the fraction decreases with the increase in the heat release rate.
The effect of air preheating on the radiant fraction in turbulent diffusion flames has been studied for both ethylene and methane as a fuel, and preheated air (up to 1230 K) as an oxidizer (Fujimori et al., 2000). The radiant fraction χr was found with the air temperature and, for ethylene (C2H4), the fraction was found to exceed 0.6 for an air temperature of 1120 K (Fig. 1). To change the amount of in-flame soot, the fuel was diluted with N2. As expected, it was found that the radiant fraction decreased rapidly with the dilution (i.e., a decrease in the mass fraction of fuel χFin the jet).

Figure 1. Effect of preheated air temperature on radiation fraction (Fujimori et al., 2000).
Modeling of Turbulent Flames
Chemically reacting turbulent flows were first simulated using the mean-property model (Faeth et al., 1989). The properties needed for the calculations are time-averaged scalar quantities, which are supplied from the predictions of the flow-thermal model (Bilger, 1976; Pope, 2000). The model assumes that turbulent fluctuations have no effect on spectral and total radiation characteristics. The mean-property model, including flame radiation, has received significant research attention, but is only briefly highlighted here.
As an illustration of the mean-property model for calculating the flame structure and radiation characteristics of a nonluminous axisymmetric turbulent flame, we follow here the analysis used by Faeth et al. (1989). The major assumptions of the analysis are as follows: (i) low-velocity (low-Mach number) flow with no swirl, (ii) equal turbulent exchange coefficients of all species and heat, (iii) buoyancy affects only the mean flow, and (iv) the absence of turbulence-radiation interactions. Under these assumptions, the conserved-scalar formulation (Bilger, 1976) can be used, relating all scalar properties to the mixture fraction through the laminar flamelet state relationships.
The governing equations for the conservation of mass, momentum, energy, and mixture fraction f, as well as additional modeled governing equations for turbulent kinetic energy k, the rate of dissipation of turbulent kinetic energy ε, and the square of the mixture fraction fluctuations g, are found from the solution of the Favre-averaged generalized equation of the form
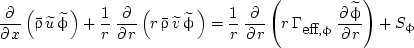
|
(2) |
where 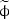 = 1, ũ,
= 1, ũ,  ,
,  , k, ε, or g. The formulation is based on Favre-averaged (mass-weighted) quantities
, k, ε, or g. The formulation is based on Favre-averaged (mass-weighted) quantities 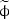 as follows:
as follows:

|
(3) |
where the overbar represents a conventional time average and P(f) is the time-averaged PDF (probability density function). Expressions for μeff,ϕ and Sϕ appearing in Eq. (2), along with all empirical constants, are available elsewhere (Faeth et al., 1989). The constants employed were established by matching predictions and measurements. Of course, the initial and boundary conditions must also be specified to complete the mathematical formulation of the problem and the solution of Eq. (3).
Mean and stochastic turbulent flame radiation models have been assessed (Faeth et al., 1989). Scalar properties of different fuel flames have been compared with available experimental data, and reasonably good agreement has been found. Spectral radiation intensity predictions based on mean and stochastic models for nonluminous and luminous turbulent flames are found to be in good agreement with data for H2-, CH4-, and C2H2-air flames (Faeth et al., 1989; Viskanta, 2005). For the acetylene-air diffusion flame, spectral radiation is dominated by strong continuum radiation from soot, but the 4.3 μm CO2 gas band is still evident.
The calculations based on the mean-property approach and the time and space series simulation approach for non-premixed and partially premixed flames were compared with each other, and the two sets of results were compared with experimental data for non-premixed and premixed flames (Zheng et al., 2003). The simulated spectral radiances, including both mean and rms, were generally within 10-20% of the measurements. Some typical spectral radiances for a partially premixed flame D at 4.27 μm(Zheng et al., 2003) are shown in Fig. 2. The mean intensifies are about five times higher at λ = 4.3 μm than at λ = 2.51 μm.The data and findings reported are of fundamental value in the assessment of radiation models for turbulent flames, which are needed for turbulent combustion simulations.

Figure 2. Comparison of measured and calculated spectral radiation intensities for premixed flame D at 4.27 μm (after Zheng et al., 2003).
Chemically Reacting Turbulent Flows with Radiation
The continuous need to improve combustion efficiency and reduce pollutant emissions has motivated the need to continue development of computational methods to accurately simulate turbulent chemically reacting flows. Reynolds-averaged Navier-Stokes (RANS) methods have been used for a long time and continue to be employed for simulation of practical combustion systems. Newer methods such as large eddy simulation (LES) and direct numerical simulation (DNS) provide enhanced accuracy and/or can resolve all turbulent scales, but with significantly higher computational requirements. Accounting for radiation in turbulent reactive flows introduces additional computational challenges.
It is well known that turbulence-radiation interaction (TRI) may significantly impact radiative transfer in chemically reactive flows and the structure of flames (Viskanta, 2005; Coelho, 2007). Three approaches have been used in modeling chemically reactive turbulent flow with radiative transfer: (i) neglect the turbulence-radiation interaction altogether, (ii) account for turbulence-radiation interaction using the optically thin fluctuation approximation, and (iii) fully account for turbulence-radiation interaction. The optically thin fluctuation approximation is based on the assumption that individual eddies in a turbulent flow are homogeneous and optically thin, and the properties of fluctuating eddies are statistically independent. The approximation does not hold for optically thick media (e.g., strongly radiating sooty flames) or for wavelengths in the vicinity of the center of strong absorption levels of radiatively participating gaseous species (Coelho, 2007). Only the third approach is discussed in the paragraphs to follow.
As an alternate to the optically thin fluctuation approximation approach, the TRI model accounts for both the spectral absorption coefficient and temperature fluctuation of the radiating gaseous fuel combustion product species (Viskanta, 2005; Coelho, 2007). We note that spectral absorption coefficient depends on the radiating species’ concentration and temperature.
The RTE for an emitting-absorbing nonscattering medium may be written as

|
(4) |
where I is the radiation intensity, κ the absorption coefficient, Ib the blackbody radiation intensity, and s the direction of propagation of radiation. The subscript ν stands for the wave number, frequency, or wavelength. In the case of a turbulent flow, numerical simulations are generally performed using the time-averaged form of the governing equations, except in the case of direct or large eddy simulations. The time-averaged form of Eq. (4) takes the following form:

|
(5) |
The term κ'νI'ν is neglected if the optically thin fluctuation approximation is used, while κν and κνIbν may be evaluated from the PDF of mixture fraction in the case of a prescribed PDF shape or computed from a PDF transport model. In fact, the absorption coefficient is a function of temperature, pressure, and molar fraction of the absorbing species, and the Planck function depends only on the temperature. The temperature and the molar fraction of the species may be determined from the mixture fraction. Therefore, if the pressure variation is small, as is often the case in incompressible flows, then κν and Ibν may also be determined from the mixture fraction. Accordingly, κν and κνIbν may be evaluated without any additional closure assumption, besides those involved in the PDF shape of mixture fraction.
It is well known that in turbulent flames, TRI may significantly increase the mean radiation intensity, and the flame temperature as well as the radiant energy loss/gain are affected (Viskanta, 2005; Coelho, 2007). This interaction has been mainly studied in the framework of RANS simulations in which the time-averaged form of the RTE needs to be solved. Large errors may occur if the TRI is ignored (Coelho et al., 2003; Li and Modest, 2003). A few recent studies have investigated TRI in turbulent non-premixed (Habibi et al., 2007; Deshmuk et al., 2007) and premixed (Wu et al., 2004) combustion. For example, Habibi et al. represented turbulence by RANS, while chemistry was modeled by means of steady laminar flamelets, and TRI was studied systematically using three different formulations. As required by DNS, the geometries and the chemical kinetics models employed by Wu et al. (2004) and Deshmukh et al. (2007) are relatively simple.
A detailed analysis of the relevance of TRI recently was carried out in the framework of LES for the turbulent reactive flows in Sandia flame D, a widely studied piloted turbulent non-premixed flame (Coelho, 2009). It is concluded that the errors resulting from neglecting TRI in LES are much smaller than those found in RANS calculations.
Recently, a novel approach for coupling large eddy simulations of turbulent combustion and radiative transfer has been proposed by Gonçalves dos Santos et al. (2008). The authors perform LES and radiative transfer calculations by two independent computer codes that exchange data when needed through a specialized interface, COBRA, using an internal computer network or over the Internet. The radiation code gets temperature and mass fraction fields from the combustion code, and returns radiative flux divergence (net loss/gain of radiant energy per unit volume). The authors claim that the coupling is easy to implement, portable, flexible, and versatile; however, the coupling may not be easy to implement since complex adaption codes must be written, and this makes the methodology less flexible and less versatile. Simulations of a turbulent premixed propane-air flame stabilized downstream of an obstacle have been reported. The preliminary results generated, taking into account radiative transfer, reveal that radiation strongly modifies the flame dynamics and leads to results that are in better agreement with experimental data. The approach has potential for enhancing the coupled large eddy simulations of turbulent combustion and radiative transfer, and should be explored further.
Radiation in Luminous Turbulent Non-Premixed Flames
Great progress continues to be made in the understanding and phenomenology of soot formation in turbulent flames. The processes are important in many practical combustion systems, and this accounts for the past research attention that the topic has received. A comprehensive review and discussion of the chemistry of soot formation, growth, and oxidation has been prepared (Kennedy, 1997). A discussion of radiation transfer in sooting turbulent flames is available (Viskanta, 2005).
In addition to the usual system of balance equations for mass, momentum, energy, mixture fraction (mean and variance), and turbulence characteristics (k and ε, for example, in case the k-ε turbulence model is used), which might be typically employed to describe Favre-averaged turbulent combustion, a simplified two-equation soot formation model that accounts for nucleation, surface growth, and coagulation has been proposed (Young and Moss, 1995),
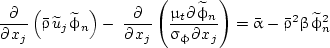
|
(6) |
and

|
(7) |
where fv is the soot volume fraction, n is the particle number density, and ϕn = n/ρN0, with N0 being the Avogadro number (6 × 1026), ϕf = (ρs/ρ)fv, and ρ and ρs denoting the local mixture and soot density, respectively. The terms α and δ identify the influence of nucleation on the number density and soot volume fraction, while β, γ, and wox denote the processes of coagulation, surface growth, and oxidation, respectively. Numerous extensions of the above model and applications to turbulent luminous flames are discussed by Kennedy (1997).
Radiative transfer in turbulent luminous flames has been studied by numerous investigators using a variety of approaches and levels of sophistication (Viskanta, 2005). For example, Leung et al. (1991) accounted for the radiation effects by assuming that a fixed fraction of the chemical energy released due to combustion is lost to the surroundings via thermal radiation. An optically thin approximation that accounts for emission by gases and soot, but neglects the effects of self-absorption, has been used by Kronenberg et al. (2000). A practical radiative transfer model for turbulent sooty flames is that of Bresloff et al. (1998). They used a DTM to solve the RTE and employed the WSGG for gas and soot emittance, but neglected turbulence-radiation interaction. Zimberg et al. (1998) simulated strongly radiating, non-premixed acetylene-air flames in stationary homogeneous turbulence, and studied coupled turbulence, soot chemistry, and radiation interactions. The linear eddy transport model is used to simulate turbulent advection, and the laminar flamelet is employed to treat combustion along with two different soot models. Radiation effects are accounted for in the thermal energy equation using the optically thin approximation, and the contribution of gases is neglected in comparison to soot in evaluating the Planck mean absorption coefficient. The volumetric radiative source/sink term is represented by

|
(8) |
where Co = 2.77 × 10-7 kW/m3K5. The fifth power dependence of temperature results from the wavelength dependence of the spectral absorption coefficient of soot (Viskanta, 2005).
Probably the most realistic and detailed simulation of radiative transfer in a sooty turbulent ethylene-air diffusion flame has been carried out by Tessé et al. (2004). Radiative transport within the sooty flame was modeled out using a Monte Carlo method, and an accurate CK model for the gas. The influence of TRI on radiative transfer has been accounted for. Contributions of soot and gas, only soot, only gas, only H2O, and only CO2 on the global radiation absorption and emission rates by the flame have been calculated both by neglecting and by considering TRI. The influence of turbulence-radiation interaction on the global radiation emission and absorption rates by the flame have been calculated without and with TRI, the uncorrelated assumption, and for different turbulent integral lengths. A hybrid model for sooting turbulent flames has been described (Aksit and Moss, 2006). A Lagrangian Monte Carlo solution for the mixture fraction and representative soot properties, coupled with a Eulerian solution for the turbulent flow field, accompanies significant computational economy by adopting the laminar flamelet approach for the source terms in the soot rate equations and the reduced number of scalars computed stochastically. Radiative transfer has not been considered in the model, but would have to be included for more realistic simulation for turbulent sooting flames.
Reference is made to a recent paper by El-Asrag et al. (2007), which describes a soot formation model in premixed flames as well as provides an extensive list of references dealing with soot formation in flames. A subgrid model for soot dynamics is developed for LES that uses a method of moments approach, and that requires no a priori knowledge of the particles’ distribution. The soot formation model is implemented within a subgrid mixing and combustion model. Radiative transfer is treated using the optically thin approximation in which absorption by soot particles as well as gaseous species (CO2 and H2O) is not considered.
REFERENCES
Aksit, I. M. and Moss, J. B., A Hybrid Scalar Model for Sooting Turbulent Flames, Combust. Flame, vol. 145, pp. 231-244, 2006.
Baukal, Jr., C. E., Gershtein, V. Y., and Li, X. (eds.), Computational Fluid Dynamics in Industrial Combustion, CRC Press, Boca Raton, 2001.
Bilger, R. W., Turbulent Jet Diffusion Flames, Prog. Energy Combust. Sci., vol. 1, pp. 87-109, 1976.
Bilger, R. W., Future Progress in Turbulent Combustion Research, Prog. Energy Combust. Sci., vol. 26, pp. 367-380, 2000.
Borghi, R., Turbulent Combustion Modeling, Prog. Energy Combust. Sci., vol. 14, pp. 245-292, 1988.
Bresslof, N. W., Moss, J. B., and Rubini, P. A., CFD Prediction of Coupled Radiation Heat Transfer and Soot Production in Turbulent Flames, Proc. Combust. Inst., vol. 26, pp. 2379-2386, 1998.
Coelho, P. J., Teerling, J., and Roekerts, D., Spectral Radiative Effects and Turbulence-Radiation Interaction in a Turbulent Jet Diffusion Flame, Combust. Flame, vol. 133, 7 pp. 5-91, 2003.
Coelho, P. J., Numerical Simulation of the Interaction between Turbulence and Radiation in Reactive Flows, Prog. Energy Combust. Sci., vol. 33, pp. 311-383, 2007.
Coelho, P. J., Approximate solutions of Filtered Radiative Transfer Equation in Large Eddy Simulations in of Turbulent Reactive Flows, Combust. Flame, vol. 156, pp. 1099-1110, 2009.
Deshmukh, K. V., Howorth, D. C., and Modest, M. F., Direct Numerical Simulation of Turbulence-Radiation Inter-One-Dimensional Non-Premixed System, J. Quant. Spectrosc. Radiat. Transfer, vol. 109, pp. 2391-2400, 2007.
El-Asrag, H., Lu, T., Law, C. K., and Menon, S., Simulation of Soot Formation in Turbulent Premixed Flames, Combust. Flame, vol. 150, pp. 108-126, 2007.
Faeth, G. M., Gore, J. P., Church, S. G., and Jeng, S.-M., Radiation from Diffusion Flames, In C. L. Tien and T. C. Chawla (eds.), Annual Review of Numerical Fluid Mechanics and Heat Transfer, Hemisphere Publishing, New York, pp. 1-38, 1989.
Fujimori, T., Hamano, Y., and Sato, J., Radiation Heat Loss and NOx Emission of Turbulent Jet Flames in Preheated Air up to 1230 K, Proc. Combust. Inst., vol. 28, pp. 455-461, 2000.
Glassman, I., Combustion, 3rd ed., Academic Press, New York, 1996.
Gonçalves dos Santos, R., Lecanu, M., Ducruix, S., Gicquel, O., Iacona, E., and Veynante, D., Coupled Large Eddy Simulations of Turbulent Combustion and Radiative Heat Transfer, Combust. Flame, vol. 152, pp. 387-400, 2008.
Habibi, A., Merci, B., and Roekaerts, D., Turbulence Radiation Interaction in Reynolds-averaged Navier-Stokes Simulations of Nonprexixed Piloted Turbulent Laboratory-Scale Flames, Combust. Flame, vol. 151, pp. 303-320, 2007.
Kennedy, L. M., Models of Soot Formation and Oxidation, Prog. Energy Combust. Sci., vol. 23, pp. 95-132, 1997.
Kronenberg, A., Bilger, R. W., and Kent, J. H., Modeling Soot Formation in Turbulent Jet Diffusion Flames, Combust. Flame, vol. 121, pp. 24-40, 2000.
Leung, K. M., Lindenstedt, R. P., and Jones, W. P., A simplified Reaction Mechanism for Soot Formation in Nonpremixed Flames, Combust. Flame, vol. 87, pp. 289-305, 1991.
Li, G. and Modest, M. F., Importance of Turbulence-Radiation Interaction in Turbulent Diffusion Jet Flames, J. Heat Transfer, vol. 125, pp. 831-838, 2003.
Pope, S. B., Turbulent Flows, Cambridge University Press, Cambridge, England, 2000.
Tessé, L., Dupoirieux, F., and Taine, J., Monte Carlo Modeling of Radiative Transfer in a Turbulent Sooty Flame, Int. J. Heat Mass Transfer, vol. 47, pp. 555-572, 2004.
Turns, S. R., An Introduction to Combustion, 2nd ed., McGraw-Hill, New York, 2000.
Viskanta, R., Radiative Transfer in Combustion Systems: Fundamental and Applications, Begell House, New York and Reddin, CT, 2005.
Williams, F. A., Combustion Theory: The Fundamental Theory of Chemically Reacting Flow Systems, 2nd ed., Benjamin/Cummings Publishing, Menlo Park, CA, 1985.
Wu, Y., Howarth, D. C., Modest, M. F., and Cuenot, B., Direct Numerical Simulation of Turbulence/Radiation Interaction in Premixed Combustion Systems. Proc. Combust. Inst., vol. 30, pp. 639-646, 2004.
Young, K. J. and Moss, J. B., Modeling Sooting Turbulent Jet Flames Using an Extended Flamelet Technique, Combust. Sci. Technol., vol. 105, pp. 33-53, 1995.
Zheng, Y., Barlow, R. S., and Gore, J. P., Measurements and Evaluations of Spectral Radiation Intensities of Turbulent Non-Premixed and Partially Premixed Flames, J. Heat Transfer, vol. 125, pp. 1065-1073, 2003.
Zimberg, J. J., Frankel, S. H., Gore, J. P., and Sivanathu, Y. R., A Study of Coupled Turbulent Mixing, Soot Chemistry and Radiation Effects Using the Linear Eddy Model, Combust. Sci. Technol, vol. 113, pp. 454-469, 1998.
Referências
- Aksit, I. M. and Moss, J. B., A Hybrid Scalar Model for Sooting Turbulent Flames, Combust. Flame, vol. 145, pp. 231-244, 2006.
- Baukal, Jr., C. E., Gershtein, V. Y., and Li, X. (eds.), Computational Fluid Dynamics in Industrial Combustion, CRC Press, Boca Raton, 2001.
- Bilger, R. W., Turbulent Jet Diffusion Flames, Prog. Energy Combust. Sci., vol. 1, pp. 87-109, 1976.
- Bilger, R. W., Future Progress in Turbulent Combustion Research, Prog. Energy Combust. Sci., vol. 26, pp. 367-380, 2000.
- Borghi, R., Turbulent Combustion Modeling, Prog. Energy Combust. Sci., vol. 14, pp. 245-292, 1988.
- Bresslof, N. W., Moss, J. B., and Rubini, P. A., CFD Prediction of Coupled Radiation Heat Transfer and Soot Production in Turbulent Flames, Proc. Combust. Inst., vol. 26, pp. 2379-2386, 1998.
- Coelho, P. J., Teerling, J., and Roekerts, D., Spectral Radiative Effects and Turbulence-Radiation Interaction in a Turbulent Jet Diffusion Flame, Combust. Flame, vol. 133, 7 pp. 5-91, 2003.
- Coelho, P. J., Numerical Simulation of the Interaction between Turbulence and Radiation in Reactive Flows, Prog. Energy Combust. Sci., vol. 33, pp. 311-383, 2007.
- Coelho, P. J., Approximate solutions of Filtered Radiative Transfer Equation in Large Eddy Simulations in of Turbulent Reactive Flows, Combust. Flame, vol. 156, pp. 1099-1110, 2009.
- Deshmukh, K. V., Howorth, D. C., and Modest, M. F., Direct Numerical Simulation of Turbulence-Radiation Inter-One-Dimensional Non-Premixed System, J. Quant. Spectrosc. Radiat. Transfer, vol. 109, pp. 2391-2400, 2007.
- El-Asrag, H., Lu, T., Law, C. K., and Menon, S., Simulation of Soot Formation in Turbulent Premixed Flames, Combust. Flame, vol. 150, pp. 108-126, 2007.
- Faeth, G. M., Gore, J. P., Church, S. G., and Jeng, S.-M., Radiation from Diffusion Flames, In C. L. Tien and T. C. Chawla (eds.), Annual Review of Numerical Fluid Mechanics and Heat Transfer, Hemisphere Publishing, New York, pp. 1-38, 1989.
- Fujimori, T., Hamano, Y., and Sato, J., Radiation Heat Loss and NOx Emission of Turbulent Jet Flames in Preheated Air up to 1230 K, Proc. Combust. Inst., vol. 28, pp. 455-461, 2000.
- Glassman, I., Combustion, 3rd ed., Academic Press, New York, 1996.
- Gonçalves dos Santos, R., Lecanu, M., Ducruix, S., Gicquel, O., Iacona, E., and Veynante, D., Coupled Large Eddy Simulations of Turbulent Combustion and Radiative Heat Transfer, Combust. Flame, vol. 152, pp. 387-400, 2008.
- Habibi, A., Merci, B., and Roekaerts, D., Turbulence Radiation Interaction in Reynolds-averaged Navier-Stokes Simulations of Nonprexixed Piloted Turbulent Laboratory-Scale Flames, Combust. Flame, vol. 151, pp. 303-320, 2007.
- Kennedy, L. M., Models of Soot Formation and Oxidation, Prog. Energy Combust. Sci., vol. 23, pp. 95-132, 1997.
- Kronenberg, A., Bilger, R. W., and Kent, J. H., Modeling Soot Formation in Turbulent Jet Diffusion Flames, Combust. Flame, vol. 121, pp. 24-40, 2000.
- Leung, K. M., Lindenstedt, R. P., and Jones, W. P., A simplified Reaction Mechanism for Soot Formation in Nonpremixed Flames, Combust. Flame, vol. 87, pp. 289-305, 1991.
- Li, G. and Modest, M. F., Importance of Turbulence-Radiation Interaction in Turbulent Diffusion Jet Flames, J. Heat Transfer, vol. 125, pp. 831-838, 2003.
- Pope, S. B., Turbulent Flows, Cambridge University Press, Cambridge, England, 2000.
- Tessé, L., Dupoirieux, F., and Taine, J., Monte Carlo Modeling of Radiative Transfer in a Turbulent Sooty Flame, Int. J. Heat Mass Transfer, vol. 47, pp. 555-572, 2004.
- Turns, S. R., An Introduction to Combustion, 2nd ed., McGraw-Hill, New York, 2000.
- Viskanta, R., Radiative Transfer in Combustion Systems: Fundamental and Applications, Begell House, New York and Reddin, CT, 2005.
- Williams, F. A., Combustion Theory: The Fundamental Theory of Chemically Reacting Flow Systems, 2nd ed., Benjamin/Cummings Publishing, Menlo Park, CA, 1985.
- Wu, Y., Howarth, D. C., Modest, M. F., and Cuenot, B., Direct Numerical Simulation of Turbulence/Radiation Interaction in Premixed Combustion Systems. Proc. Combust. Inst., vol. 30, pp. 639-646, 2004.
- Young, K. J. and Moss, J. B., Modeling Sooting Turbulent Jet Flames Using an Extended Flamelet Technique, Combust. Sci. Technol., vol. 105, pp. 33-53, 1995.
- Zheng, Y., Barlow, R. S., and Gore, J. P., Measurements and Evaluations of Spectral Radiation Intensities of Turbulent Non-Premixed and Partially Premixed Flames, J. Heat Transfer, vol. 125, pp. 1065-1073, 2003.
- Zimberg, J. J., Frankel, S. H., Gore, J. P., and Sivanathu, Y. R., A Study of Coupled Turbulent Mixing, Soot Chemistry and Radiation Effects Using the Linear Eddy Model, Combust. Sci. Technol, vol. 113, pp. 454-469, 1998.