Chemical reaction is a process of conversion of some chemical compounds into others. In general, chemical reaction can be represented by the equation
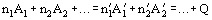
where Ai are the reactants;
 are the products; ni and
are the products; ni and
 are the corresponding stoichiometric coefficients; and Q is the thermal effect of the reaction. Both reactants and products can be atoms, molecules or charged particles (ions or electrons); in photochemical reactions, photons are included as well. The sign of Q can be positive (which means that heat is evolving through the reaction; such reactions are called exothermic) or negative (when heat is absorbed through the reaction; such reactions are called endothermic). The thermal effect of the reaction does not depend on the method of transformation from reactants to products (Hess' law, 1836).
are the corresponding stoichiometric coefficients; and Q is the thermal effect of the reaction. Both reactants and products can be atoms, molecules or charged particles (ions or electrons); in photochemical reactions, photons are included as well. The sign of Q can be positive (which means that heat is evolving through the reaction; such reactions are called exothermic) or negative (when heat is absorbed through the reaction; such reactions are called endothermic). The thermal effect of the reaction does not depend on the method of transformation from reactants to products (Hess' law, 1836).
Any chemical reaction proceeds simultaneously in two directions: forward and reverse. At equilibrium, both reactions have the same rates, thus the rate of the total process is equal to zero. The relationship between concentrations (or partial pressures for reactions in the gaseous state) at equilibrium is called the mass action law (Huldberg and Waage, 1867):

or

where pnii(Ai)[or cnii(Ai)] are the partial pressures (concentrations) of Ai and Kp(T)[or Kc(T)] is the equilibrium constant which depends on the temperature T, but does not depend on partial pressures (concentrations) of the components Ai. Strictly, the mass action law can be applied only to the ideal case where no interaction occurs between the molecular particles of the gas or the solute. This assumption is usually justified for gaseous reactions if the total pressure is not considerably higher than 0.1 MPa. Generally, it is not applied to reactions in the solution phase, except for very dilute solutions. The more correct form of this law applied to real systems requires the inclusion of fugacity fi instead of the partial pressure pi, or activity ai instead of concentrations ci.
When doing mass action law calculations, a distinction must be drawn between homogeneous and heterogeneous reactions. A homogeneous reaction is one which takes place completely in one phase, such as H2 + I2 = 2HI, or
 . For them, the mass action law can be written as:
. For them, the mass action law can be written as:

and

where Kp and Kc are the mass action constants at a certain temperature, p denotes partial pressure and c is the molar concentration. In heterogeneous reactions, one or more condensed phases appear in addition to the gaseous or solution phase. The mass action relationship is then expressed as in the following example for the reaction Fe2O3(cr) + 3C(cr) = 2Fe(1) + 3CO(g):

In practice, equilibrium can be shifted when only the products of the reaction are present and the concentration of the reactants is so small that it can be neglected. In this case, only the forward reaction takes place. These reactions are called kinetic one-sided or kinetic unreversible. In such reactions, one of the products formed is constantly removed, thereby continuously displacing the system from equilibrium.
Written in its usual form, the equation of a chemical reaction shows only the initial and final states of the process. This equation can be considered as a symbolic expression of the mass action law. Actually, many reactions proceed through a series of intermediate stages. These individual stages may be referred to as elementary reactions. In most cases, the exact mechanism of the reaction is unknown because of the difficulty in correctly revealing all the intermediate products which the reaction is going through.
The rate of reaction v is proportional to the concentrations of each substance [A1], [A2], … participating in the reaction raised to a power which is equal to a corresponding stoichiometric coefficient n1, n2, …:

This equation is often called the mass action law for the rate of the chemical process. The factor k is the rate constant of the chemical reaction. For simple reactions, the degrees n1, n2, … are integer. Each of these values is called the order of the reaction for a given substance. The sum N = n1 + n2 + … is called the overall order of the reaction. For more complex reactions, this expression can also be applied, but the order of such a reaction may not be an integer. For example, consider a reaction with reactants A1 and A2. If the reaction is of the first order in A1 and the first order in A2, the overall order of the reaction is equal to two.
There are reactions of zero order, in which the rate is unaffected by changes in the concentrations of one or more reactants because it is determined by some limiting factor other than concentration, such as the amount of light absorbed through a photochemical reaction or the amount of catalyst in a catalytic reaction.
To determine the change of the concentrations of the components with time for the case of a complex chemical reaction, the system of differential equations must be solved. This system is defined through the reaction mechanism and the equations of material balance, and usually can be very complicated. If a multistage process proceeds through the formation of short-lived molecules, the initial differential equation system can be simplified assuming that dc/dt = 0 for these molecules, and thus facilitate the process of solving the system.
The dimensions of the rate constants depends on the order of the reaction N and on the dimensions of the concentration. Concentrations are usually expressed either in a number of molecules per unit of volume (m−3) or in a number of moles of the substance per m3 (mol m−3). The units of the rate constant k for chemical reactions of the overall order N can be expressed by the general formula (m3mol−1)N − 1s−1.
The dependence of the rate constant on temperature is given by the Arrhenius equation (1889)

where A is a factor which may also vary with temperature, Ec is the energy of activation, k is the Boltzmann constant and T is the absolute temperature. The exponential dependence of the rate constant on temperature had been detected experimentally before Arrhenius, but he was the first who proposed its theoretical interpretation. According to his hypothesis, molecules whose energy exceed Ea are the only ones undergoing chemical conversion. The fraction of such molecules in a Boltzmann distribution is directly proportional to exp(−Ea/kT). The dependence of (the constant A on temperature can be described by the relation A = A0Tn, where n is defined by the characteristics of a process.
Calculation of rate constants is the typical task of the theory of elementary chemical processes. The process of chemical reaction depends on the electronic, vibrational, and rotational states of the colliding particles participating in the reaction. If the density of gas is not too high, the time of the collision (10−12 − 10−19s) is sufficiently smaller than the time between the collisions of the molecules (10−10s under normal conditions). Therefore, the problem can be separated in two parts: determination of the reaction cross-sections s and microscopical rate constants (i.e., the value which characterizes the rates of reaction for a particle in a given state), on the one hand, and evaluation of the partition function F of molecules, on the other. Such a problem is usually very difficult to solve. In the method of transitional states, the following basic assumptions are used:
The phase space of the molecular system is divided into parts which correspond to the reactants, products and intermediate species;
These parts of phase space are separated by critical surfaces. The region of phase space which corresponds to the location of the system on the critical surface is called an activated complex;
Concentration of the activated complex is assumed to be at equilibrium and can be calculated;
The rate of the elementary process coincides with the flux from the region of reactants into the region of products.
Using all these assumptions, the rate constant of the chemical reaction can take the following form:

This is the basic formula of the transitional states method; Z and Z≠ are the partition functions for the initial molecular system and transitional state, respectively. The transmission factor χ in a classical case cannot be greater than 1. Since the calculation of the value of χ is a rather difficult problem, the critical surface is usually chosen so that χ is equal to 1.
Chemical reactions are usually classified in correspondence with the number of molecules participating in each elementary chemical process. The reaction in which only one molecule undergoes chemical transformation is called monomolecular. The most typical transformation of this kind is a reaction of thermal dissociation. If the pressure is high enough, the reaction will be of the first order; if the pressure is low, the order of the reaction is close to two. Bimolecular reactions form the most common class of chemical reactions. In these reactions, both colliding particles undergo chemical transformation. Usually the reactions are of the second order. The simplest process of this class is a reaction of A+ BC = AB + C. In trimolecular reactions, all three particles in collision undergo chemical transformation. Under normal conditions, the rate of such reactions is approximately two orders less than for bimolecular ones. Therefore, trimolecular reactions occur very rare. A classical example of this reaction is 2NO2 + X2 = 2NOX, where X is the halogen or oxygen atom.
In open systems, the rate of concentration change of a substance is not equal to the rate of the chemical reaction, and mass transfer should been taken into account.
REFERENCES
Benson, S. W. (1976) Thermochemical Kinetics. 2nd ed. John Wiley and Sons, Inc.
Daniels, F. and Alberty, R. A. (1975) Physical Chemistry. 4th ed. John Wiley and Sons, Inc.
参考文献
- Benson, S. W. (1976) Thermochemical Kinetics. 2nd ed. John Wiley and Sons, Inc.
- Daniels, F. and Alberty, R. A. (1975) Physical Chemistry. 4th ed. John Wiley and Sons, Inc.