RADIATIVE TRANSFER FOR COUPLED ATMOSPHERE AND OCEAN SYSTEMS: OVERVIEW
Leading to: Radiative transfer for coupled atmosphere and ocean systems: the discrete ordinate method
A beam of radiation propagating in a turbid medium can be scattered, absorbed, or re-emitted. For simplicity, the inelastic process that involves radiation energy transfer from one wavelength to others is not considered in this article. The radiative transfer equation (RTE) is introduced to describe these interaction processes phenomenologically (Chandrasekhar, 1960; Preisendorfer, 1965). The derivation of the RTE from the classical Maxwell equations has also been published (Mishchenko et al., 2006). The RTE has important applications in many fields (Kattawar, 1991; Dombrovsky, 1996; Liou, 2002; Marshak and Davis, 2005; Modest, 2003). In this article, we are particularly interested in the radiative transfer process in a coupled atmosphere and ocean system (AOS), which plays an essential role in ocean color remote sensing, the general circulation model, and many other studies (Mobley, 1994; Thomas and Stamnes, 1999).
The RTE is a differential-integral equation that can be solved analytically only in a few cases (Chandrasekhar, 1960). Mostly, one has to rely on numerical techniques. As an introductory and educational effort, contributors of this series will discuss the methods of discrete ordinate (DISORT), successive order of scattering (SOS), doubling and adding, and Monte Carlo (MC). We will also introduce a hybrid method. Note that this is not a complete list of methods. There are a few other methods, for instance, the spherical harmonics method (Kourganoff, 1952; Garcia and Siewert, 1986), the multicomponent method (Zege et al., 1993; Zege and Chaikovskaya, 1996), the spherical harmonics discrete ordinate method (Evans, 1998, 2007), and the FN method (Garcia and Siewert, 1989; Wauben and Hovenier, 1992). Mobley et al. (1993) have compared a few numerical models for underwater radiance simulations. We will introduce the RTE and the boundary conditions for the AOS in this article. The methods of DISORT, SOS, Monte Carlo, and hybrid will be presented in the following series.
Consider a beam of light with radiant energy dEλ within a small solid angle dΩ that crosses an area element dA in time dt. The subscript λ means that energy is within the wavelength interval of (λ, λ + dλ). The angle between the normal vector of the area element and the light propagation direction is θ. The radiance of light is then defined as
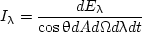
|
(1) |
Also, we will drop the subscript λ from now on, but always keep in mind that I is wavelength dependent. The monochromatic irradiance is defined by
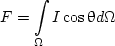
|
(2) |
which is interpreted as the power per unit area per unit wavelength interval that passes across the area element.
If the beam of light propagates in a homogenous turbid medium, the radiance will decrease due to scattering and absorption. The amount of decrease dI is proportional to the radiance I and the propagation distance ds (see Fig. 1 for the coordinate system with direction s defined in terms of zenith angle θ and azimuth angle ϕ),

|
(3) |
where βe is called the extinction coefficient. The extinction coefficient is the sum of the absorption βa and scattering βs coefficients: βe = βa + βs. On the other hand, the radiance could also increase because of emission from the medium and multiple scattering from other directions. The amount of increase dI can be written in the following way:
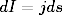
|
(4) |
where j is the source function

|
(5) |
P is the phase function that describes the angular distribution of the scattered radiance. B is the Planck function representing the thermal emission. The phase function satisfies the normalization condition,

|
(6) |
The overall change dI of radiance is the sum of Eqs. (3) and (4),
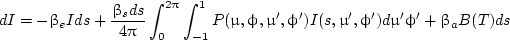
|
(7) |
Now, we limit ourselves to the case of plane parallel medium in which the optical properties are allowed to change only in the z dimension (see Fig. 1). Now, it is convenient to introduce the concept of optical depth τ, which is a dimensionless quantity defined by
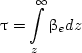
|
(8) |
so that dτ = -βedz, ds = dz/μ, where μ = cosθ and θ is the zenith angle of the directions of propagation. The RTE can then be written in the following format:
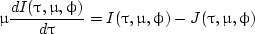
|
(9) |
where
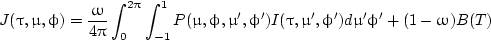
|
(10) |
and ω = βs/βe is the single-scattering albedo. Equation (10) assumes the scattering properties P, ω, and temperature T are constants in the medium. If variation of these quantities is desired, one can simply replace P(θ,ϕ) by P(τ,θ,ϕ), ω by (ωτ), and T by T(τ) in Eq. (10).

Figure 1. Coordinate system with definitions of zenith and azimuth angles.
An integral form of Eq. (9) can be written as (Liou, 2002)

|
(11) |
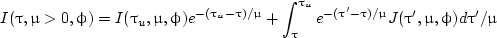
|
(12) |
where τl < τ < τu; τl and τu are used to denote the lower and upper boundaries of the plane-parallel medium, respectively.
For simplicity, the polarization is ignored in this article. If polarization is desired, the radiance I will be replaced by the Stokes parameters (I,Q,U,V), where the first component I is the same as the radiance, Q and U contain the linear polarization information, and V is the circular polarization component. Accordingly, the 4 × 4 phase matrix will take the place of the phase function. The readers are referred to the references for further information (Chandrasekhar, 1960).
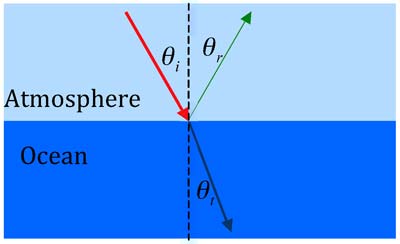
The focus of this article is to introduce the radiative transfer theory in the coupled atmosphere and ocean system. The key part is how light interacts with the dielectric interface between the atmosphere and ocean. It is well known that light will be reflected and refracted by the interface. Here, the primary task is to quantify the reflection and refraction (transmission) processes in terms of radiance and irradiance. In other words, we need to find the boundary conditions related to the interface. There are two cases we need to deal with, namely, flat [see Fig. 2(a)] or rough [see Fig. 2(b)] ocean surfaces. The boundary conditions for a calm (flat) ocean are simple, while those for a rough (wavy) ocean are relatively lengthy and complicated. In this section, we will introduce the boundary conditions for both cases.
|

|
| (a) | (b) |
Figure 2. (a) An atmosphere and ocean system with flat ocean surface; (b) an atmosphere and ocean system with rough ocean surface.
Consider a beam of light incident at a flat ocean surface. It is then reflected and refracted by the ocean surface. There are three angles associated with the scenario, i.e., the angles of incidence θi, reflection θr, and refraction θt. These angles are defined as the angles between the normal vector of the flat surface and the incident, reflected, and transmitted light rays. It is well known that θi = θr, and nisinθi = ntsinθt (Snell’s law), where ni and nt are the refractive index of the incident and transmitted media, respectively. In general, the index of refraction is a complex quantity. In this series, we assume it is a real number in the atmosphere as well as in the ocean. The incident, reflected, and transmitted light rays are all contained within one plane, which is called the incident plane. If the light is incident from the air, the values are ni ≈ 1 and nt = nw, where nw is the refractive index of water. If light is incident from the water, the values are ni = nw and nt ≈ 1. The symbols Ii, Ir, and It are used to denote the radiances of incident, reflected, and transmitted lights. The relations between them for a flat surface are then

|
(13a) |

|
(13b) |

|
(13c) |

|
(13d) |
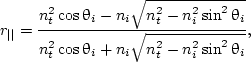
|
(13e) |
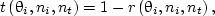
|
(13f) |
where r(θi,ni,nt) and t(θi,ni,nt) are the reflection and transmission coefficients, respectively. r|| and r⊥ are Fresnel’s reflection coefficients for the electric fields that are parallel or perpendicular to the incident plane. The factor (nt/ni)2 in Eq. (13b) is due to the n-squared law for radiance across a dielectric interface, which is a net consequence of changes of the solid angle and projected area before and after the light passes across the interface. We are referring readers to page 159 of Mobley (1994) for the detailed derivation. Thoughtful readers may now begin to doubt that the n-squared law violates the law of energy conservation. Indeed, the n-squared law only applies to the radiances across a dielectric interface. If the irradiances are calculated by integrating the radiances across the interface, the energy conservation law is actually satisfied. Furthermore, r(θi,ni,nt) and t(θi,ni,nt) will be replaced by 4 × 4 matrices if polarization is included (Zhai et al., 2010).
The reflection and refraction of a beam of light by a flat surface have been covered so far. Now, we consider the case in which there are diffuse radiance fields at both sides of the interface. The relations between the diffuse radiance fields across a dielectric interface are called the interaction principles (Mobley, 1994). The term Ia(θ,ϕ) denotes the diffuse radiance field in the atmosphere just above the interface, and Iw(θ,ϕ) stands for the diffuse radiance field in the ocean just below the interface. Also, it is understood that θ < 90 deg or μ = cosθ > 0, corresponding to upwelling radiance, and vise versa. The boundary conditions of the dielectric interface say the following:
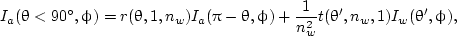
|
(14a) |
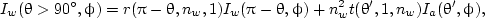
|
(14b) |
where θ and θ' satisfy Snell’s law, i.e., nisinθ' = ntsinθ. Equation (14a) means that the upwelling radiance just above the interface is equal to the sum of the reflection of the downwelling atmospheric radiance and transmission of the upwelling oceanic radiance, while Eq. (14b) says that the downwelling radiance just below the interface is equal to the sum of transmission from downwelling atmospheric radiance and reflection from upwelling oceanic radiance.
The flat interface is an important ideal case to illustrate the optical principles. In reality, however, the presence of ocean waves is almost certain. Thus, it is meaningful to discuss the boundary conditions across a rough ocean surface. If a rough surface is present, the reflected/refracted light of a monodirectional beam light will now spread over a range of solid angle [see Fig. 2(b)]. To describe the distribution of the light after interaction with the interface, the bidirectional reflection distribution function (BRDF) Br(μ,ϕ,μ',ϕ') and bidirectional transmission distribution function (BTDF) Bt(μ,ϕ,μ',ϕ') are introduced. Consider a beam of light with irradiance E' at direction (μ',ϕ') incident on a dielectric interface. The reflected radiance is denoted by Ir(μ,ϕ) in the direction (μ,ϕ). The BRDF Br is defined as

|
(15a) |
Similarly, the BTDF is defined in terms of the transmitted radiance It(μ,ϕ) as

|
(15b) |
If the BRDF and BTDF are known, we can find Ir and It easily from Eqs. (15). To obtain the BRDF and BTDF, we may start with an appropriate ocean surface model. The pioneer work of Cox and Munk (1954) describes the rough ocean surface as a collection of water facets, whose normal vectors follow a Gaussian distribution. Figure 3 shows a schematic drawing of a segment of rough ocean surface (blue line). The black arrow stands for a local normal vector of the ocean surface. The zenith angle of the normal vector is θn, and the azimuth angle is ϕn (not shown in the figure). The wave slope statistics can be written as
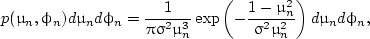
|
(16) |
where μn = cosθn, and p(μn,ϕn)dμndϕn is the probability of wave vector falls in the interval of (μn,μn + dμn) and (ϕn,ϕn + dϕn). In other words, p(μn,ϕn) is the probability density function for the ocean wave in terms of μn and ϕn. The variance σ2 is parametrized in terms of wind speed W (in meters per second) at 12 m above the ocean surface as
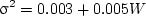
|
(17) |

Figure 3. A rough ocean surface with incident and reflected rays.
It can be shown that the BRDF can be written as (Mishchenko and Travis, 1997; Jin et al., 2006; Lenoble, 2007; Zhai et al., 2010)
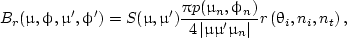
|
(18) |
where θi is the incident angle formed by the anti-incident direction (μ',π - ϕ') and the local surface normal (μn,ϕn). It can be conveniently calculated by θi(π - Θ)/2, and

|
(19) |
S(μ,μ') is the shadowing function (Smith, 1967; Sancer, 1969),
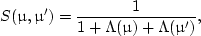
|
(20a) |
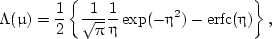
|
(20b) |

|
(20c) |
where erfc is the complementary error function (Gautsch, 1964). The shadowing function is to consider part of a rough surface may be blocked by other part of the surface if viewing from either the incident or reflected direction of the light.
The BTDF is (Zhai et al., 2010)

|
(21) |
where θi is the incident angle, and nisinθ = ntsinθt. For the case of air incidence, we have
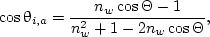
|
(22a) |

|
(22b) |
where Θ is the scattering angle given by Eq. (19). For the case of water incidence, the expressions of cosθi and cosθt will be exchanged as
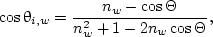
|
(23a) |

|
(23b) |
The interaction principles for a rough surface can be obtained from the following definitions of BRDF and BTDF:

|
(24a) |
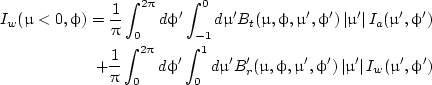
|
(24b) |
in which B'r and B't denote the BRDF and BTDF for the water incidence case.
REFERENCES
Chandrasekhar, S., Radiative Transfer, Dover, New York, 1960.
Cox, C. and Munk, W., Measurement of the Roughness of the Sea Surface from Photographs of the Sun’s Glitter, J. Opt. Soc. Am., vol. 44, pp. 838-850, 1954.
Dombrovsky, L. A., Radiation Heat Transfer in Disperse Systems, Begell House, New York and Redding, CT, 1996.
Evans, K. F., The Spherical Harmonic Discrete Ordinate Method for Three-Dimensional Atmospheric Radiative Transfer, J. Atmos. Sci., vol. 55, pp. 429-446, 1998.
Evans, K. F., SHDOMPPDA: A Radiative Transfer Model for Cloudy Sky Data Assimilation, J. Atmos. Sci., vol. 64, pp. 3858-3868, 2007.
Garcia, R. D. M. and Siewert, C. E., A Generalized Spherical Harmonics Solution for Radiative Transfer Models that Include Polarization Effects, J. Quant. Spectrosc. Radiat. Transfer, vol. 36, pp. 401-423, 1986.
Garcia, R. D. M. and Siewert, C. E., The FN Method for Radiative Transfer Models that Include Polarization Effects, J. Quant. Spectrosc. Radiat. Transfer, vol. 41, pp. 117-145, 1989.
Gautsch, W., Error Function and Fresnel Integrals, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematics Tables, vol. 55, Abramowitz, M. and Stegun, I. A., (eds.), National Bureau of Standards; Washington, pp. 295-329, 1964.
Jin, Z., Charlock, T. P., Rutledge, K., Stamnes, K., and Wang, Y., Analytical Solution of Radiative Transfer in the Coupled Atmosphere-Ocean System with a Rough Surface, Appl. Opt., vol. 4, pp. 7443-7455, 2006.
Kattawar, G. W., Multiple Scattering in Plane Parallel Atmospheres and Oceans: Techniques, SPIE Press, Bellingham, 1991.
Kourganoff, V., Basic Methods in Transfer Problems, Clarendon Press, London, 1952.
Lenoble, J., Herman, M., Deuz&eakute;, J. L., Lafrance, B., Santer, R., and Tanr&eakute;, D., A Successive Order of Scattering Code for Solving the Vector Equation of Transfer in the Earth’s Atmosphere with Aerosols, J. Quant. Spectrosc. Radiat. Transfer, vol. 107, pp. 479-507, 2007.
Liou, K. N., An Introduction to Atmospheric Radiation, 2nd ed., Academic Press, New York, 2002.
Marshak, A. and Davis, A. B. (eds.), 3D Radiative Transfer in Cloudy Atmospheres, Springer, New York, 2005.
Mishchenko, M. I. and Travis, L. D., Satellite Retrieval of Aerosol Properties over the Ocean Using Polarization as Well as Intensity of Reflected Sunlight, J. Geophys. Res., vol. 102, pp. 16989-17013, 1997.
Mishchenko, M. I., Travis, L. D., and Lacis, A. A., Multiple Scattering of Light by Particles, Cambridge University Press, New York, 2006.
Mobley, C. D., Gentili, B., Gordon, H. R., Jin, Z., Kattawar, G. W., Morel, A., Reinersman, P., Stamnes, K., and Stavn, R.H., Comparison of Numerical Models for Computing Underwater Light Fields, Appl. Opt., vol. 32, pp. 7484-7504, 1993.
Mobley, C. D., Light and Water: Radiative Transfer in Natural Waters, Academic Press, New York, 1994.
Modest, M. F., Radiative Heat Transfer, 2. ed., Academic Press, New York, 2003.
Preisendorfer, R. W., Radiative Transfer on Discrete Spaces, Pergamon Press, Oxford, 1965.
Sancer, M. I., Shadow-Corrected Electromagnetic Scattering from a Randomly Rough Surface, IEEE Trans. Antennas Propagat., 17, pp. 577-585, 1969.
Smith, B. G., Geometrical Shadowing of a Random Rough Surface, IEEE Trans. Antennas Propagat., vol. 15, pp. 668-671, 1967.
Thomas, G. E. and Stamnes, K., Radiative Transfer in the Atmosphere and Ocean, Cambridge University Press, Cambridge, UK, 1999.
Wauben, W. M. F. and Hovenier, J. W., Polarized Radiation of an Atmosphere Containing Randomly Oriented Spheroids, J. Quant. Spectrosc. Radiat. Transfer, vol. 47, pp. 491-504, 1992.
Zege, E. P., Katsev, I. L., and Polonsky, I. N., Multicomponent Approach to Light Propagation in Clouds and Mists, Appl. Opt., vol. 32, pp. 2803-2812, 1993.
Zege, E. P. and Chaikovskaya, L. I., New Approach to the Polarized Radiative Transfer Problem, J. Quant. Spectrosc. Radiat. Transfer, vol. 55, pp. 19-31, 1996.
Zhai, P., Hu, Y., Chowdhary, J., Trepte, C. R., Lucker, P. L., and Josset, D. B., A Vector Radiative Transfer Model for Coupled Atmosphere and Ocean Systems with a Rough Interface, J. Quant. Spectrosc. Radiat. Transfer, vol. 111, 1025-1040, 2010.
参考文献
- Chandrasekhar, S., Radiative Transfer, Dover, New York, 1960.
- Cox, C. and Munk, W., Measurement of the Roughness of the Sea Surface from Photographs of the Sun’s Glitter, J. Opt. Soc. Am., vol. 44, pp. 838-850, 1954.
- Dombrovsky, L. A., Radiation Heat Transfer in Disperse Systems, Begell House, New York and Redding, CT, 1996.
- Evans, K. F., The Spherical Harmonic Discrete Ordinate Method for Three-Dimensional Atmospheric Radiative Transfer, J. Atmos. Sci., vol. 55, pp. 429-446, 1998.
- Evans, K. F., SHDOMPPDA: A Radiative Transfer Model for Cloudy Sky Data Assimilation, J. Atmos. Sci., vol. 64, pp. 3858-3868, 2007.
- Garcia, R. D. M. and Siewert, C. E., A Generalized Spherical Harmonics Solution for Radiative Transfer Models that Include Polarization Effects, J. Quant. Spectrosc. Radiat. Transfer, vol. 36, pp. 401-423, 1986.
- Garcia, R. D. M. and Siewert, C. E., The FN Method for Radiative Transfer Models that Include Polarization Effects, J. Quant. Spectrosc. Radiat. Transfer, vol. 41, pp. 117-145, 1989.
- Gautsch, W., Error Function and Fresnel Integrals, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematics Tables, vol. 55, Abramowitz, M. and Stegun, I. A., (eds.), National Bureau of Standards; Washington, pp. 295-329, 1964.
- Jin, Z., Charlock, T. P., Rutledge, K., Stamnes, K., and Wang, Y., Analytical Solution of Radiative Transfer in the Coupled Atmosphere-Ocean System with a Rough Surface, Appl. Opt., vol. 4, pp. 7443-7455, 2006.
- Kattawar, G. W., Multiple Scattering in Plane Parallel Atmospheres and Oceans: Techniques, SPIE Press, Bellingham, 1991.
- Kourganoff, V., Basic Methods in Transfer Problems, Clarendon Press, London, 1952.
- Lenoble, J., Herman, M., Deuz&eakute;, J. L., Lafrance, B., Santer, R., and Tanr&eakute;, D., A Successive Order of Scattering Code for Solving the Vector Equation of Transfer in the Earth’s Atmosphere with Aerosols, J. Quant. Spectrosc. Radiat. Transfer, vol. 107, pp. 479-507, 2007.
- Liou, K. N., An Introduction to Atmospheric Radiation, 2nd ed., Academic Press, New York, 2002.
- Marshak, A. and Davis, A. B. (eds.), 3D Radiative Transfer in Cloudy Atmospheres, Springer, New York, 2005.
- Mishchenko, M. I. and Travis, L. D., Satellite Retrieval of Aerosol Properties over the Ocean Using Polarization as Well as Intensity of Reflected Sunlight, J. Geophys. Res., vol. 102, pp. 16989-17013, 1997.
- Mishchenko, M. I., Travis, L. D., and Lacis, A. A., Multiple Scattering of Light by Particles, Cambridge University Press, New York, 2006.
- Mobley, C. D., Gentili, B., Gordon, H. R., Jin, Z., Kattawar, G. W., Morel, A., Reinersman, P., Stamnes, K., and Stavn, R.H., Comparison of Numerical Models for Computing Underwater Light Fields, Appl. Opt., vol. 32, pp. 7484-7504, 1993.
- Mobley, C. D., Light and Water: Radiative Transfer in Natural Waters, Academic Press, New York, 1994.
- Modest, M. F., Radiative Heat Transfer, 2. ed., Academic Press, New York, 2003.
- Preisendorfer, R. W., Radiative Transfer on Discrete Spaces, Pergamon Press, Oxford, 1965.
- Sancer, M. I., Shadow-Corrected Electromagnetic Scattering from a Randomly Rough Surface, IEEE Trans. Antennas Propagat., 17, pp. 577-585, 1969.
- Smith, B. G., Geometrical Shadowing of a Random Rough Surface, IEEE Trans. Antennas Propagat., vol. 15, pp. 668-671, 1967.
- Thomas, G. E. and Stamnes, K., Radiative Transfer in the Atmosphere and Ocean, Cambridge University Press, Cambridge, UK, 1999.
- Wauben, W. M. F. and Hovenier, J. W., Polarized Radiation of an Atmosphere Containing Randomly Oriented Spheroids, J. Quant. Spectrosc. Radiat. Transfer, vol. 47, pp. 491-504, 1992.
- Zege, E. P., Katsev, I. L., and Polonsky, I. N., Multicomponent Approach to Light Propagation in Clouds and Mists, Appl. Opt., vol. 32, pp. 2803-2812, 1993.
- Zege, E. P. and Chaikovskaya, L. I., New Approach to the Polarized Radiative Transfer Problem, J. Quant. Spectrosc. Radiat. Transfer, vol. 55, pp. 19-31, 1996.
- Zhai, P., Hu, Y., Chowdhary, J., Trepte, C. R., Lucker, P. L., and Josset, D. B., A Vector Radiative Transfer Model for Coupled Atmosphere and Ocean Systems with a Rough Interface, J. Quant. Spectrosc. Radiat. Transfer, vol. 111, 1025-1040, 2010.