A coordinate system is a system of surfaces in n-dimensional space which allows the association of every point in that space point with an ordered set of numbers (ξ1, ξ2, ... , ξn) (in customary three-dimensional space—three numbers (ξ1, ξ2, ξ3). The proper choice of a coordinate system in a mathematical description of a process in some volume can significantly simplify its mathematical formulation and problem solution.
Cartesian (rectangular) coordinates are formed by three families of self-perpendicular planes: x = const; y = const; z = const. If one puts three other families of surfaces, which are not parallel with each other, on this system, then the location of every point (x,y,z) can be defined by a crossing of three surfaces from these families, which form a new system of curvilinear coordinates. If the surfaces of curvilinear coordinates are described by the equations ξ(x,y,z) = const, ξ2(x,y,z) = const, ξ3(x,y,z) = const, the location of some point is fixed by coordinates (ξ1, ξ2, ξ3), as well as by coordinates (x,y,z). The Jacobian transformation (x,y,z) → (ξ1, ξ2, ξ3), which is a coefficient of an elementary volume change through the transformation, isn't equal to zero.
The distance between two close points is predicted as:
where Hij are the Lamé coefficients, describing the metrics of the coordinate system.
For orthogonal coordinate systems with self-perpendicular coordinate surfaces, Hij = 0 for i ≠ j and
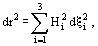
where Hi = Hii. Then, the values of surface and volume elements are:
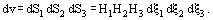
In orthogonal coordinate systems, a function gradient is written as:
where
, are unit vectors normal to surfaces ξi = const
A vector divergence is written as:
a Laplacian function
Components of a vector rotor are:
In the Cartesian coordinate system, x,y,z H1 = H2 = H3 = 1.
In a cylindrical coordinate system, ρ, φ, z (x = ρ cos φ, y = ρ sin φ, z = z), H1 = 1, H2 = r. H3 = 1 (an equivalent coordinate system on a plane ρ, φ is called the polar coordinate system).
In a spherical coordinate system, r, θ, φ (x = ρ sin θ cos φ, y = ρ sin θ sin φ, z = ρ cos θ) Hi = 1, H2 = r, H3 = r sin θ.
For some problems characterized by particular volume geometry, some other coordinate systems can be employed, such as ellipsoidal (elliptic), paraboloidal, bicylindrical (bipolar), conical, etc.