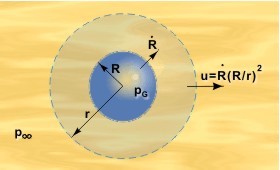
Vapor bubble growth in a superheated liquid is part of the process of nucleate boiling. It is also related to depressurization (flashing) processes. The early stages of bubble growth — when the bubble is still microscopic — are complicated by the uncertainties surrounding the nucleation process itself, and by the fact that the excess pressure due to surface tension across the liquid-vapor interface, 2σ/R, is comparable with the pressure difference driving bubble growth pG − p∞ . Once this initial period is over the process of bubble growth, in a uniformly superheated liquid at least, is straightforward.
Obviously, a vapor bubble in a superheated liquid is unstable. It will grow while superheated liquid remains. There are two main constraints to the rate of growth. There is the inertia of the surrounding liquid, which has to be pushed out of the way, and there is the need for heat to diffuse from the surrounding liquid to the interface to cause evaporation.
Inertia-controlled growth is more likely to exist in the early stages, particularly at low pressures when only a small amount of heat is needed to create a large volume of vapor. If the bubble radius is R then, as shown in Figure 1, the velocity of the bubble boundary is

Continuity requires that the outward flow rate of liquid at every radius r is the same, i.e.,

where u is the velocity at r.
The kinetic energy of this moving liquid is:

This energy is supplied by the expanding vapor. Oversimplifying the derivation, with vapor pressure pG expanding against the external pressure p∞, it yields

Equating expressions 1 and 2 gives

and the bubble radius is given by

which is essentially the solution originally derived, much more rigorously, by Rayleigh in 1917. The pressures can be replaced by temperatures using the Clausius–Clapeyron equation, i.e.,

In practice the diffusion, heat transfer controlled, regime is more important. The solution has been obtained by Plesset and Zwick (1954). One may observe that to supply the latent heat required for a bubble of radius R, the heat has to diffuse over a distance proportional to R. The time taken to diffuse such a distance is itself proportional to R2, so the expected solution is:

The Plesset and Zwick solution gives B as

where Ja is the Jacob number given by:

A particularly convenient solution, that avoids the problem of deciding whether Eq. (4) or (6) is the more appropriate has been given by Mikic et al. in 1970. Defining the dimensionless variables

the solution is

which in the limit of t+ << 1 gives Eq. (4) and for t+ >> 1 gives Eq. (6).
Most practical situations do not involve isolated bubbles surrounded by infinite seas of uniformly superheated liquid. One complication, with bubble growth on a solid surface, is that the spread of vapor over the surface often leaves a microlayer of liquid behind. The effect of this microlayer on bubble growth is discussed in the article on nucleate boiling.
Recent papers that discuss more complex situations include one that analyzes a bubble on a wall in a linear temperature gradient, taking into account the effect of the wall thermal conductivity [Klimenko (1989)], and another that assumes a falling liquid pressure, i.e., depressurization {Wang and Bankoff (1991)].
REFERENCES
Fyodorov, M. V. and Klimenko, V. V. (1989) Vapor bubble growth in boiling under quasi-stationary heat transfer condition in a heating wall, Int. J. Heat Mass Transfer, 32:227–242. DOI: 10.1016/0017-9310(89)90170-1
Mikic, B. B., Rohsenow, W. M., and Griffith, P. (1970). On bubble growth rates, Int. J. Heat Mass Transfer, 13:657–666.
Plesset, M. S. and Zwick, J. A. (1954) Growth of vapour bubbles in superheated liquids, J. Applied Phys. 25:493.
Rayleigh, L. (1917) Pressure due to Collapse of Bubbles, Phil. Mag. 34:94
Wang, Z. and Bankoff, S. G. (1991) Bubble growth on a solid wall in a rapidly depressurizing liquid pool, Int. J. Multiphase Flow, 17:425–437. DOI: 10.1016/0301-9322(91)90040-A
Les références
- Fyodorov, M. V. and Klimenko, V. V. (1989) Vapor bubble growth in boiling under quasi-stationary heat transfer condition in a heating wall, Int. J. Heat Mass Transfer, 32:227–242. DOI: 10.1016/0017-9310(89)90170-1
- Mikic, B. B., Rohsenow, W. M., and Griffith, P. (1970). On bubble growth rates, Int. J. Heat Mass Transfer, 13:657–666.
- Plesset, M. S. and Zwick, J. A. (1954) Growth of vapour bubbles in superheated liquids, J. Applied Phys. 25:493.
- Rayleigh, L. (1917) Pressure due to Collapse of Bubbles, Phil. Mag. 34:94
- Wang, Z. and Bankoff, S. G. (1991) Bubble growth on a solid wall in a rapidly depressurizing liquid pool, Int. J. Multiphase Flow, 17:425–437. DOI: 10.1016/0301-9322(91)90040-A