In the following entry, Rotating Disc Systems, Basic Phenomena are classified in terms of the parameter Γ, the ratio of the speed of the slower disc to that of the faster one. The main application of these systems is to model the conditions found inside the wheel-space of gas-turbine-engines, where the cases Γ = 0, +1 and –1 are the most important. The rotor-stator system (Γ = 0) is used to model the flow and heat transfer associated with an air-cooled turbine disc and an adjacent stationary casing; the rotating cavity (Γ = +1) is used to model conditions between corotating turbine or compressor discs; contra-rotating discs (Γ = –1) are used to model the wheel-space between the contra-rotating turbine discs of some existing (or future) engines.
The designer of internal air systems needs to know the heat transfer coefficients and frictional windage of the discs, the pressure drop of the cooling air, and the amount of air required to prevent, or reduce to safe levels, the ingress of hot mainstream gas past the rim seals into the wheel-space. For these practical cases, the gap ratio (or ratio of the axial clearance, s, to disc radius, b) is of the order of s/b = 10–1, for which clearances there are usually separate boundary layers on the two discs. The flow is turbulent throughout most of the wheel-space, but it is often instructive to study the laminar flow cases in advance of the turbulent ones.
A number of nondimensional variables are used to characterize these flows, and the most useful of these are defined below:


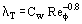


Here Ω is the angular speed of the disc, b the radius of the disc, V the coolant volumetric flow rate (positive for radial outflow and negative for inflow), M the factional moment (or windage torque) on one side of the rotating disc, 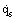 the heat flux from the disc surface to the fluid, and ΔT a representative temperature difference; r is radius, λ thermal conductivity, ρ fluid density and ν kinematic viscosity. Reφ, Cw, λT, Cm and Nu are referred to, respectively, as the rotational Reynolds Number, the nondimensional flow rate, the turbulent flow parameter, the moment coefficient and the local Nusselt Number.
the heat flux from the disc surface to the fluid, and ΔT a representative temperature difference; r is radius, λ thermal conductivity, ρ fluid density and ν kinematic viscosity. Reφ, Cw, λT, Cm and Nu are referred to, respectively, as the rotational Reynolds Number, the nondimensional flow rate, the turbulent flow parameter, the moment coefficient and the local Nusselt Number.
For engine applications, Reφ and λT are of the order of 107 and 10–1, respectively. A value of λT 0.22 is associated with the free-disc entrainment rate: the flow rate entrained by a disc rotating in a quiescent fluid. For most turbine-disc cooling applications, λT < 0.22.
0.22 is associated with the free-disc entrainment rate: the flow rate entrained by a disc rotating in a quiescent fluid. For most turbine-disc cooling applications, λT < 0.22.
Many of these (axisymmetric) rotating-disc flows have been successfully computed by a variety of methods using the integral equations, differential boundary-layer equations and elliptic solvers. In the latter case, the low-Reynolds-number k- turbulence model has proved particularly effective, and it is that model that is used here to compute the streamlines of the various flow structure. Comprehensive accounts of the cases for Γ = 0 and Γ = +1 are given by Owen and Rogers (1989, 1995).
turbulence model has proved particularly effective, and it is that model that is used here to compute the streamlines of the various flow structure. Comprehensive accounts of the cases for Γ = 0 and Γ = +1 are given by Owen and Rogers (1989, 1995).
Figure 1 shows computed streamlines for Γ = 0 and Reφ = 1.25 × 106 for a) Cw = 0 and b) Cw = 9688.
For Cw = 0 (the enclosed rotor-stator system), there is radial outflow in a thin boundary layer on the rotor (at z = 0) and inflow in a boundary layer on the stator (at z = s). Between the boundary layers, the inviscid core rotates in quasi-solid-body rotation (at about 40% the speed of the rotor) and there is an axial flow from the stator to the rotor. In the inviscid core, the Taylor-Proudman theorem applies so that u∞ = 0, ∂v∞/∂z = 0 and dw∞/∂z = 0, where u, v and w, respectively, refer to the radial, tangential and axial components of velocity relative to a rotating frame, and the subscript ∞ refers to conditions in the core. This flow structure, which occurs in laminar as well as turbulent flow, is often referred to as Batchelor-type flow after Batchelor (1951).
For Cw > 0, a source region is formed near the inlet where the incoming fluid is entrained into the boundary layer on the rotor. If the incoming fluid has no swirl, then there is no rotation in the source region, and the core rotation is less than that associated with Cw = 0. The radial extent of the source region increases as λT increases, and for λT ≥ 0.22 the source region fills the entire system. Both Cm and Nu depend on λT: for λT = 0.22, Cm is equal to that of the free disc; for λT = 0, Cm is approximately half that of the free disc.
The rotating flow in the core can create a negative pressure inside the wheel-space, allowing the ingress of hot mainstream gas. A minimum nondimensional flow rate, Cw,min is required to prevent this ingress, which depends on the rim-seal geometry, on Reφ, and on the conditions inside the mainstream gas itself. The ingress problem is discussed extensively by Owen and Rogers (1989).
Computed streamlines for isothermal rotating cavities with a radial outflow and inflow of cooling air are shown in Figure 2 for Γ = +1 and Reφ = 1.1 × 106 for a) Cw = +1500 (radial outflow) and b) Cw = –1500 (radial inflow). For both cases, the fluid enters the cavity without swirl.
Referring to Figure 2a, fluid enters the cavity at r = a forming a source region, that distributes the flow into Ekman-type layers on each disc, and leaves via a sink layer at r = b that distributes the flow into a slot or holes in the peripheral rotating shroud. In the rotating inviscid core between the Ekman-type layers, the Taylor-Proudman theorem applies and, consequently, the axial and radial components of velocity are zero.
Fluid is entrained into the boundary layers in the source region, and the (nonentraining) Ekman-type layers start where all the available fluid has been entrained: the tangential velocity of the core, which is lower than that of the discs, adjusts to ensure that the mass flow rate in the Ekman-type layers is invariant with radius.
For the case of heated discs, the Nusselt numbers increase radially in the entraining boundary layers in the source region and decrease in the nonentraining Ekman-type layers, reaching a maximum value near the outer edge of the source region. As for the rotor-stator case, the size of the source region increases as λT increases.
Referring to Figure 2b, fluid enters through the rotating shroud at r = b, forming a source region, and leaves at r = a, via a sink layer. Outside the source region, where all the available fluid is entrained into the boundary layers, nonentraining Ekman-type layers are formed on the discs. The Taylor-Proudman theorem holds in the inviscid core, which rotates faster than the discs.
As well as depending on λT, the size and structure of the source region depends strongly on the inlet swirl ratio, c, where c is the ratio of the tangential speed of the incoming fluid to that of the discs at r = b. If c > 1, the flow is radially inward throughout the cavity. If c < 1, the flow in the boundary layers in the source region is radially outward where the fluid rotates slower than the discs and radially inward where it rotates faster. Consequently, for c < 1, there is recirculation in the source region as shown in Figure 2b: mixing between the recirculating flow and the fluid entering the cavity causing the effective swirl ratio, ceff, to be larger than the inlet swirl ratio, c. The angular momentum of the fluid in the source region is virtually conserved resulting in quasi-free-vortex flow. Outside the source region, the tangential velocity corresponds to that required to maintain a constant flow rate in the Ekman-type layers.
Radial-inflow presents more problems than outflow, and the complex structure of the source region makes computation of the flow and heat transfer more difficult. The large tangential velocities generated by the free-vortex-type flow mean that the radial pressure gradients in the rotating cavity can be large. The flow rate of turbine-cooling air depends on the pressure difference between the compressor and the turbine: the pressure drop created by radial inflow can significantly reduce the coolant flow rate.
For the radial inflow and outflow cases, the flow rates used in gas turbines are usually large enough to ensure that (axisymmetric) forced convection dominates. For the case of a rotating cavity with no superposed flow or with an axial throughflow of cooling air, buoyancy effects are usually significant: the flow can then become nonaxisymmetric and unsteady, and the Nusselt numbers are significantly smaller than for the forced convection cases.
For the case of a sealed cavity where one disc is hot and other cold, fluid flows radially outward in a boundary layer on the cold disc and radially inward on the hot disc. Such flows can be axisymmetric and steady. For the cases of a sealed cavity where the outer cylindrical casing (or shroud) is hot and the inner one cold, free convection takes place through a system of cyclonic and anti-cyclonic vortices, as described in Part 1. These vortices create circumferential regions of low and high pressure which provide the necessary Coriolis forces to allow simultaneous radial inflow and outflow of fluid between the hot and cold surfaces.
The axial throughflow case is further complicated by the possibility of vortex breakdown. This is the abrupt change in the structure of an axial jet of swirling fluid which, in the case of a rotating cavity, can create nonaxisymmetric, unsteady flow even under isothermal conditions. The interaction between a central jet undergoing vortex breakdown and buoyancy-induced flow in the cavity itself makes this case the Everest of the rotating-disc problems: it is a challenge to both computational and experimental research workers!
Figure 3 shows computed streamlines for T = –1 and Reφ = 1.19 × 106 for a) Cw = 0 and b) Cw = 9350.
For Cw = 0, there is radial outflow in the boundary layers on the rotating discs and radial inflow in the core between the boundary layers. The core is virtually nonrotating (so the Taylor-Proudman theorem does not apply), and this flow structure is often referred to as Stewartson-type flow after Stewartson (1953), (For laminar flow, Batchelor (1951) predicted a flow structure with contra-rotating cores; this can be computed but it does not appear to exist in practice.)
For Cw = 9350, a source region is formed near the inlet where the incoming (nonswirling) fluid is entrained into the boundary layers on the discs. Outside the source region, recirculation occurs in a similar way to that described above for Cw = 0. The moment coefficients for Γ = –1 can be up to twice the magnitude of those for Γ = 0, but the difference decreases as Cw increases.
If, as is customary, the Nusselt number is defined using the temperature difference, ΔT, between the surface of the disc and the fluid at inlet to the system then Nu for Γ = –1 is less than Nu for Γ = 0. This apparent contradiction of the Reynolds Analogy (see Part 1) is caused by the use of inappropriate reference temperatures.
The double transition from laminar to turbulent flow and from Batchelor-type flow at Γ = 0 to Stewartson-type flow at Γ = –1 has been investigated by Kilic et al. (1994). For –1 < Γ < 0, a two-cell structure occurs with Batchelor-type flow (with a rotating core) in the (radially) outer cell and Stewartson-type flow (with a nonrotating core) in the inner one. If Γ is reduced, the relative sizes of cells change until at Γ = –1 there is only Stewartson-type flow.
The flow and heat transfer for Γ = –1 appears to remain axisymmetric under all observed conditions, and agreement between computed and measured values is mainly good.
REFERENCES
Batehelor, G. K. (1951) Note on a class of solutions of the Navier-Stokes equations representing steady rotationally-symmetric flow, Quart. J Mech. Appl. Math., 4, 29–41.
Kilic, M., Gan, X. and Owen, J. M. (1994) Transitional flow between contra-rotating discs, J. Fluid Mech. 281, 119–135.
Owen, J. M. and Rogers, R. H. (1989) Flow and Heat Transfer in Rotating Disc Systems, Vol. 1: Rotor-stator systems, Research Studies Press, Taunton, John Wiley, New York.
Owen, J. M. and Rogers, R. H. (1995) Flow and Heat Transfer in Rotating Disc Systems, Vol. 2: Rotating cavities, Research Studies Press, Taunton, John Wiley, New York.
Stewartson, K. (1953) On the flow between two rotating coaxial discs, Proc. Camb. Phil. Soc., 49, 333–341.
Les références
- Batehelor, G. K. (1951) Note on a class of solutions of the Navier-Stokes equations representing steady rotationally-symmetric flow, Quart. J Mech. Appl. Math., 4, 29–41. DOI: 10.1093/qjmam/4.1.29
- Kilic, M., Gan, X. and Owen, J. M. (1994) Transitional flow between contra-rotating discs, J. Fluid Mech. 281, 119–135. DOI: 10.1017/S0022112094003058
- Owen, J. M. and Rogers, R. H. (1989) Flow and Heat Transfer in Rotating Disc Systems, Vol. 1: Rotor-stator systems, Research Studies Press, Taunton, John Wiley, New York.
- Owen, J. M. and Rogers, R. H. (1995) Flow and Heat Transfer in Rotating Disc Systems, Vol. 2: Rotating cavities, Research Studies Press, Taunton, John Wiley, New York.
- Stewartson, K. (1953) On the flow between two rotating coaxial discs, Proc. Camb. Phil. Soc., 49, 333–341.


