RADIATIVE TRANSFER IN COUPLED ATMOSPHERE AND OCEAN SYSTEMS: THE ADDING AND DOUBLING METHOD
Following from: Radiative transfer in coupled atmosphere and ocean systems: the Successive Order of Scattering method
Leading to: Radiative transfer in coupled atmosphere and ocean systems: the Monte Carlo method
We have been using the concepts of the bidirectional reflection distribution function (BRDF) and bidirectional transmission distribution function (BTDF) for a rough surface. In this section, it is necessary to extend the concepts to a layer of general scattering medium. If a layer of media is illuminated by a monodirectional source light from the top, the scattered light will exit the layer from either the top (reflection) or bottom (transmission) of the layer. Then, the BRDF for the scattering layer is defined by the reflected light from the top and the incident light in a similar way as Eq. (15a) in Zhai and Hu (2011),
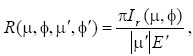
|
(1a) |
where E′ is the incident irradiance perpendicular to the propagation direction, μ′ is the cosine of the incident zenith angle, and Ir is the diffuse light exiting from the top of the scattering layer. The BTDF for the same scattering layer is defined by

|
(1b) |
where It is the transmitted light at the bottom of the layer. If the scattering layer is illuminated from below, the reflection and transmission functions is denoted as R* and T*.
Now, suppose there are two layers of scattering media and the reflection and transmission for both layers are known. The reflection and transmission from the combined layer can be obtained by computing the successive reflection between the two layers. If the two layers are identical, the results can be computed rapidly. This procedure is called doubling. Stokes (1862) has used a similar physical principle to treat the reflection and transmission of a stack of glass plates. Van de Hulst (1963) and Grant and Hunt (1969) are among the early publications on the adding method. Note that another method for the RTE called the matrix operator method is essentially the same as the adding and doubling method, at least from the computational point of view (Plass et al., 1973; Kattawar et al., 1973). A review of the adding and doubling method has been given by Hansen and Travis (1974). Wiscombe (1976) has extended the doubling and adding method to treat inhomogeneous sources within layers. Recent developments include Wauben et al. (1994) and Liu and Weng (2006). Particularly, Chowdhary et al. (2006) have used the adding and doubling method to solve the polarized RTE in the AOS (Chowdhary, 1999).
Figure 1(a) shows a visual explanation of the adding method. There are two layers of media with optical depths of τa and τb. The BRDF and BTDF for the top layer are Ra and Ta, respectively. For the lower layer, we change the subscript a to b. Also, we will use a superscript asterisk to denote the BRDF and BTDF for both layers if illuminated from below. The total reflection from the combined layer is the sum of a series of successive reflections R = R1 + R2 + R3 + L, and the total transmission is T = T1 + T2 + T3 + L. This way, the total reflection R and transmission T can be conveniently expressed in terms of the reflection and transmission of the two layers [see Eq. (3.23) in Hansen and Travis (1974)] as


Figure 1. (a) The successive reflections and transmissions between two layers of media and (b) three-layer definition in the AOS for the use with the adding and doubling method

|
(2a) |
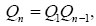
|
(2b) |

|
(2c) |

|
(2d) |

|
(2e) |

|
(2f) |

|
(2g) |
where μ0 and μ are the cosines of the incident and exiting zenith angles, respectively. The quantities Qn, S, D, U, R, and T in Eqs. (2) are functions of (μ, φ, μ′, φ′). The multiplications of these quantities imply an integration over adjoining angles. Therefore, a general expression of Z = XY can be written explicitly as

|
(3) |
A general plane-parallel scattering medium can be divided into thin sub–scattering layers, and the reflection and transmission for a very thin layer can be analytically obtained by using the single-scattering approximation [Eqs. (6.4.7a) and (6.4.7b) in Liou (2002)]. A more accurate method of obtaining it was shown by Kattawar et al. (1973). Therefore, the reflection and transmission of the finite thickness layer can be obtained by summing up thin optical depth layers one after another according to Eqs. (2). A general solution to the RTE is then obtained.
For the case of AOS, one could treat the atmosphere as one layer with the understanding that an inhomogeneous atmosphere is allowed by putting together homogenous sublayers. Similarly, the ocean body could be treated as one layer. The ocean interface is a degenerate layer with infinitesimal optical depth. After the reflection and transmission of the atmosphere and ocean are solved separately, the total reflection and transmission from the three-layer system can be solved by first combining atmosphere and interface layers, then adding the ocean layer into the system [see Fig 1(b)]. The BRDF and BTDF of the rough ocean interface have been presented in Zhai and Hu (2011). Here, we have outlined the ideas of the adding and doubling method to solve the RTE in the AOS. More information on the topic could be found in Chowdhary (1999), Chowdhary et al. (2006), and He et al. (2010).
REFERENCES
Chowdhary, J., Multiple Scattering of Polarized Light in Atmosphere-Ocean Systems, PhD, Columbia University, New York, 1999.
Chowdhary, J., et al., Contribution of Water-Leaving Radiances to Multiangle Multispectral Polarimetric Observations over the Open Ocean: Bio-Optical Model Results for Case 1 Waters, Appl. Opt., vol. 45, pp. 5542-5567, 2006.
Grant, I. P. and Hunt, G. E., Discrete Space Theory of Radiative Transfer. II. Stability and Non- Negativity, Proc. R. Soc. Lond. A, vol. 313, pp. 199-216, 1969.
Hansen, J. E. and Travis, L. D., Light Scattering in Planetary Atmospheres, Space Sci. Rev., vol. 16, pp. 527-610, (1974).
He, X., et al., A Vector Radiative Transfer Model of Coupled Ocean-Atmosphere System Using Matrix-Operator Method for Rough Sea-Surface, J. Quant. Spectrosc. Radiat. Transfer, vol. 111, no. 10, pp. 1426-1448, (2010).
Kattawar, G. W., et al., Matrix Operator Theory of Radiative Transfer, 2: Scattering from Maritime Haze, Appl. Opt., vol. 12, pp. 1071-1084, 1973.
Liou, K. N., An Introduction to Atmospheric Radiation, 2nd ed., Academic Press, New York 2002.
Liu, Q. and Weng, F., Advanced Doubling-Adding Method for Radiative Transfer in Planetary Atmospheres, J. Atmos. Sci., vol. 63, pp. 3459-3465, 2006.
Plass, G. N., et al., Matrix Operator Theory of Radiative Transfer, 1: Rayleigh Scattering, Appl. Opt., vol. 12, pp. 314-329, 1973.
Stokes, G. G., On the Intensity of the Light Reflected from or Transmitted through a Pile of Plates, Proc. Roy. Soc. London, vol. 11, pp. 545-556, 1862.
Twomey, S., et al, Matrix Methods for Multiple-Scattering Problems, J. Atmos. Sci., vol. 23, pp. 289-296, 1966.
van de Hulst, H. C., A New Look at Multiple Scattering, Tech. Rep., Goddard Institute for Space Studies, Report No. NASA TM- I03044, 1963.
Wauben, W., et al., A Method for Computing Visible and Infrared Polarized Monochromatic Radiation in Planetary-Atmospheres, Astron. Astrophys., vol. 282, pp. 277-XXX, 1994.
Wiscombe, W. J., Extension of the Doubling Method to Inhomogeneous Sources, J. Quant. Spectrosc. Radiat. Transfer, vol. 16, pp. 477-489, 1976.
Zhai, P. and Hu, Y., Radiative Transfer for Coupled Atmosphere and Ocean Systems: Overview, Thermopedia, 2011.
References
- Chowdhary, J., Multiple Scattering of Polarized Light in Atmosphere-Ocean Systems, PhD, Columbia University, New York, 1999.
- Chowdhary, J., et al., Contribution of Water-Leaving Radiances to Multiangle Multispectral Polarimetric Observations over the Open Ocean: Bio-Optical Model Results for Case 1 Waters, Appl. Opt., vol. 45, pp. 5542-5567, 2006.
- Grant, I. P. and Hunt, G. E., Discrete Space Theory of Radiative Transfer. II. Stability and Non- Negativity, Proc. R. Soc. Lond. A, vol. 313, pp. 199-216, 1969.
- Hansen, J. E. and Travis, L. D., Light Scattering in Planetary Atmospheres, Space Sci. Rev., vol. 16, pp. 527-610, (1974).
- He, X., et al., A Vector Radiative Transfer Model of Coupled Ocean-Atmosphere System Using Matrix-Operator Method for Rough Sea-Surface, J. Quant. Spectrosc. Radiat. Transfer, vol. 111, no. 10, pp. 1426-1448, (2010).
- Kattawar, G. W., et al., Matrix Operator Theory of Radiative Transfer, 2: Scattering from Maritime Haze, Appl. Opt., vol. 12, pp. 1071-1084, 1973.
- Liou, K. N., An Introduction to Atmospheric Radiation, 2nd ed., Academic Press, New York 2002.
- Liu, Q. and Weng, F., Advanced Doubling-Adding Method for Radiative Transfer in Planetary Atmospheres, J. Atmos. Sci., vol. 63, pp. 3459-3465, 2006.
- Plass, G. N., et al., Matrix Operator Theory of Radiative Transfer, 1: Rayleigh Scattering, Appl. Opt., vol. 12, pp. 314-329, 1973.
- Stokes, G. G., On the Intensity of the Light Reflected from or Transmitted through a Pile of Plates, Proc. Roy. Soc. London, vol. 11, pp. 545-556, 1862.
- Twomey, S., et al, Matrix Methods for Multiple-Scattering Problems, J. Atmos. Sci., vol. 23, pp. 289-296, 1966.
- van de Hulst, H. C., A New Look at Multiple Scattering, Tech. Rep., Goddard Institute for Space Studies, Report No. NASA TM- I03044, 1963.
- Wauben, W., et al., A Method for Computing Visible and Infrared Polarized Monochromatic Radiation in Planetary-Atmospheres, Astron. Astrophys., vol. 282, pp. 277-XXX, 1994.
- Wiscombe, W. J., Extension of the Doubling Method to Inhomogeneous Sources, J. Quant. Spectrosc. Radiat. Transfer, vol. 16, pp. 477-489, 1976.
- Zhai, P. and Hu, Y., Radiative Transfer for Coupled Atmosphere and Ocean Systems: Overview, Thermopedia, 2011.