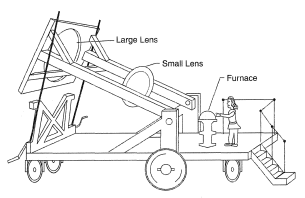
A furnace is a device in which heat is generated and transferred to materials with the object of bringing about physical and chemical changes. The source of heat is usually combustion of solid, liquid or gaseous fuel, or electrical energy applied through resistance heating (Joule heating) or inductive heating. However, solar energy can provide a clean source of high temperature if focused onto a small area. This was recognized over two hundred years ago by Lavoisier who built a large mobile "magnifying glass" system, Figure 1, to bring about the combustion of metals in a sealed glass container and subsequently the demise of the phlogiston theory.
Furnaces employing combustion produce a hot gas which transfers heat to the material by radiation and convection. Solids are heated by direct contact, but fluids are usually heated indirectly, being carried inside pipes within the furnace. Alternatively, a Regenerative Heat Exchanger may be used to transfer heat from the combustion gases. Indirect heating has the advantage of avoiding contamination by combustion products.
There are two principle categories of indirect heating furnace. The first is that of Boilers, where the heat is used to generate steam for power generation or process plant use. The second is that of furnaces designed to heat process fluids other than water. Some of the latter category are conventional heaters used simply to increase the fluid temperature, others are process heaters used to bring about physical and chemical changes in the products, for example distillation, and pyrolysis of hydrocarbons or catalytic steam-gas reforming of synthetic natural gas.
In the petrochemical industry process furnaces, or process heaters, are usually fired by oil or gas. They are designed to ensure that the fluid receives the right amount of heat and has the required residence time within specified temperature limits. This is achieved by appropriate disposition of tubes and careful control of firing rate and fluid flow. The following Figure 2 shows three typical geometries.
The following tables give the properties of gaseous, liquid and solid fuels used in furnaces. Gross calorific value includes the heat released by the condensation and cooling of combustion products, and the combustion air/fuel ratio is the stoichiometric value based on theoretically perfect combustion (see Combustion). In practice, excess air is required to ensure complete combustion. The excess is usually about 10% of the stoichiometric value for premixed gaseous fuels, 20% for distillate oil and pulverized coal, and 30% for residual oil, although lower values may be achieved with efficient burners.
The rate of heat released in a fuel fired furnace is given by the product of the mass rate of feed of fuel,
 , and the calorific value Δhf, i.e.,
, and the calorific value Δhf, i.e.,

The heat generated by combustion appears initially as sensible heat in the gaseous products of combustion, generated at the rate
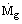 . If this were an adiabatic process (i.e., no heat transfer), the gas would attain the adiabatic flame temperature, Tf, given by
. If this were an adiabatic process (i.e., no heat transfer), the gas would attain the adiabatic flame temperature, Tf, given by

where T0 is the inlet air/fuel temperature and cpg an appropriate averaged specific heat capacity of the gases for the range T0 to Tf.
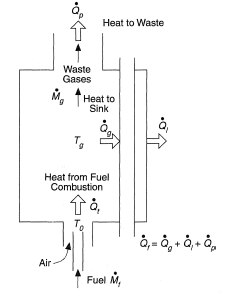
However, as illustrated in Figure 3, part of the heat generated passes to the tubes containing the process fluid at rate
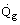 and part is lost through the furnace walls at rate
and part is lost through the furnace walls at rate
 . The remainder escapes at rate
. The remainder escapes at rate
 as waste heat of the combustion products leaving the furnace. The overall heat balance therefore is
as waste heat of the combustion products leaving the furnace. The overall heat balance therefore is

Because of this the actual gas temperature, Tg, reached in the furnace is less than the adiabatic flame temperature, Tf. Neglecting wall losses an approximate value of Tg can be obtained from

For example, in a typical oil fired furnace the value of Tf is 2,200 K and the value of Tg is 1,300 K [Shires, Hewitt and Bott (1994)].
Table 2. Properties of selected liquid and solid fuelsa
 |
| (aFrom the Heat Exchanger Design Handbook, Hemisphere Publications. With permission.) |
The rate of heat transfer,
 , from the hot gases to the tubes is a function of the gas temperature as well as the radiation properties of the gases, the geometry of the furnace and tubes, and the emissivity of the tube surface. In applying simple furnace models iteration is therefore necessary.
, from the hot gases to the tubes is a function of the gas temperature as well as the radiation properties of the gases, the geometry of the furnace and tubes, and the emissivity of the tube surface. In applying simple furnace models iteration is therefore necessary.
In most process heaters, the major part of the heat transfer from the hot gases to the tubes is by radiation. To calculate the radiative component it is necessary to know the effective emissivity, εg, of the combustion gases (typical value 0.25). This is dependent on the ratio of the partial pressures of CO2 and H2, the temperatures of the gas and the radiation source and the effective size of the radiating gas cloud. The latter is represented by the term pLo, the product of partial pressure and effective length of the furnace—a term first introduced by H. C. Hottel. For details of the procedure see Hottel and Sarofim (1967) and Hewitt, Shires and Bott (1994).
The rate of heat transfer to the furnace product is also a function of the geometry of the tube banks and the fraction of the furnace surface area covered by them.
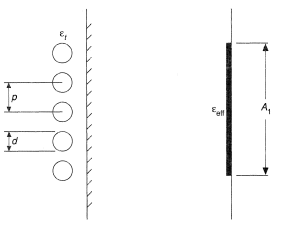
If the effective area of the tubes, A1, is only a small fraction of the total area. At, (Figure 4a), the surface receives blackbody radiation (see Radiative Heat Transfer) and the rate of heat transfer is independent of gas emissivity, εg, i.e.,

where ε1 is the effective emissivity of the receiving surface and T1 its temperature and σ is the Stefan-Boltzmann constant, 5.670 × 10−8 W/m2K4. On the other hand, if A1 is almost equal to the total surface area, At, then

Intermediate ratios are covered by the speckled surface equation [Hottel and Sarofim (1967)].

where C = A1/At.
In practice the area, A1, receiving radiation is a tube bank, Figure 5, which intercepts only a fraction of the incident radiation; some passes through to the refractory wall and is re-irradiated. For a detailed analysis see Hottel and Sarofim (1967).
The fraction of radiation intercepted by a single row of tubes having a pitch to diameter ratio B (equals p/d) is given by

Figure 6 shows F as a function of B for one and two rows of tubes.

Figure 6. Fraction of incident radiation intercepted by tubes. (From the Heat Exchanger Design Handbook, Hemisphere Publications. With permission.)
The effective emissivity based on the projected area using Eq. (7) and allowing for re-irradiation from the refractory backing is

This is illustrated in Figure 7 for a typical tube surface emissivity of 0.85.
The relationship between the rate of heat transfer,
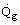 , from the gas to the tubes and the gas temperature, Tg, is obtained by combining Eqs. (6), (7) and (8). This in turn can be combined with Eq. (3) to determine the furnace thermal characteristics. An example of this procedure is described in Hewitt, Shires and Bolt (1994).
, from the gas to the tubes and the gas temperature, Tg, is obtained by combining Eqs. (6), (7) and (8). This in turn can be combined with Eq. (3) to determine the furnace thermal characteristics. An example of this procedure is described in Hewitt, Shires and Bolt (1994).
The complete mathematical description of a practical furnace is complex, combining aerodynamics, chemical reactions and heat transfer, and computer programs are normally used for detailed solutions. There are two basic types of approach; zone methods and flux methods.
Zone methods are employed when the heat release pattern from the flame is known or can be calculated independently. Conceptually, the furnace and its walls are divided into discrete zones, the effective exchange areas between zones are determined, and radiative heat transfer corresponding to the prescribed heat release pattern is calculated.
In flux methods, instead of dividing the space into zones the radiation arriving at a point in the system is itself divided into a number of characteristic directions, representing averages over a specified solid angle. Flux methods are well suited for use in combination with modern methods of prediction of fluid flow and mixing. Simultaneous solutions of the radiative heat transfer equations using flux methods and turbulent flow models are feasible.
For further information on these two methods see Beer (1974), and Afgan and Beer (1974), where examples of their application can be found.
As a first approach to the estimation of furnace performance the well stirred furnace model is relatively simple and quick to use. One of the first versions was introduced by Lobo and Evans (1939), and was used by Kern (1986). An improved version expressed in nondimensional terms was introduced by Hottel and Sarofim (1967). This was reveiwed by Hottel (1974) and subsequently described by Truelove (1983), and Hewitt, Shires and Bott (1994).
The general performance equation for furnaces derived from this model is

where




and

where d is a factor to account for imperfect mixing, approximately equal to 1.2, Te is external temperature, Ur is overall heat transfer coefficient for the refractory wall, Ar is the area of the refractory surface, A1 is the area of tube subject to radiative heat transfer, Ac is the area of tube subject to convective heat transfer and α the average convective heat transfer coefficient for Ac.
Figure 8a shows graphically the well stirred furnace model performance prediction for zero wall losses, and Figure 8b for the same conditions but with typical wall losses included. Comparison of these figures shows that wall losses have a very significant effect when tube temperatures are high. As the firing rate, represented by D'd, is reduced, the efficiency, represented by
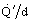 , reaches a peak then falls, eventually approaching zero as the major part of the heat is lost through the walls.
, reaches a peak then falls, eventually approaching zero as the major part of the heat is lost through the walls.

Figure 8. Performance curves for stirred reactor furnace with negligible wall losses. (From the Heat Exchanger Design Handbook, Hemisphere Publications. With permission.)

Figure 9. Performance curves for stirred reactor furnace with wall losses;
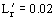 ,
,
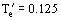 . (From the Heat Exchanger Design Handbook, Hemisphere Publications. With permission.)
. (From the Heat Exchanger Design Handbook, Hemisphere Publications. With permission.)
REFERENCES
Afgan, N. H. and Beer, J. M. (1974) Heat Transfer in Flames, Scripta Book Co., Wiley, New York.
Beer, J. M. (1974) Methods of calculating radiative heat transfer from flames in combustors and furnaces, Heat Transfer in Flames, Scripta Book Co., Wiley, New York.
Hewitt, G. F. Shires, O. L., and Bott T. R. (1994) Process Heat Transfer, CRC Press.
Hottel, H. C. (1974) First estimates of industrial performance; the one—gas—zone model re-examined, Heat Transfer in Flames, Scripta Book Co., Wiley, New York.
Hottel, H. C. and Sarofim, A. F. (1967) Radiative Heat Transfer, McGraw-Hill, New York.
Kern, D. O. (1986) Process Heat Transfer, McGraw-Hill, New York.
Lobo, W. E. and Evans, J. E. (1939) Trans AIChE, 35-743.
Truelove, J. S. (1983) Furnaces and combustion chambers. Heat Exchanger Design Handbook, Hemisphere Publishing, New York.
References
- Afgan, N. H. and Beer, J. M. (1974) Heat Transfer in Flames, Scripta Book Co., Wiley, New York.
- Beer, J. M. (1974) Methods of calculating radiative heat transfer from flames in combustors and furnaces, Heat Transfer in Flames, Scripta Book Co., Wiley, New York.
- Hewitt, G. F. Shires, O. L., and Bott T. R. (1994) Process Heat Transfer, CRC Press.
- Hottel, H. C. (1974) First estimates of industrial performance; the one—gas—zone model re-examined, Heat Transfer in Flames, Scripta Book Co., Wiley, New York.
- Hottel, H. C. and Sarofim, A. F. (1967) Radiative Heat Transfer, McGraw-Hill, New York.
- Kern, D. O. (1986) Process Heat Transfer, McGraw-Hill, New York.
- Lobo, W. E. and Evans, J. E. (1939) Trans AIChE, 35-743.
- Truelove, J. S. (1983) Furnaces and combustion chambers. Heat Exchanger Design Handbook, Hemisphere Publishing, New York.