Evaporative cooling is one of the most efficient techniques for thermal protection (see Ablation and Sublimation). It is based on the application of two mechanisms of heat absorption: phase conversion of a heat protective coating and the injection of gaseous products of decomposition of the coating into the boundary layer surrounding a body with a high-velocity and high-temperature gas flow around it. With increased incoming flow enthalpy He, the role of the second mechanism grows and becomes predominant.
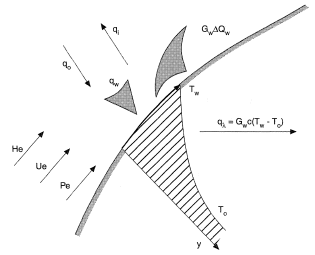
Consider the heat balance on a destructing surface (Figure 1). The convective heat flux  (equal to the product of (α/cp) and the enthalpy drop across the boundary layer (He – Hw), where α is the heat transfer coefficient) leads to a rise in the body’s surface temperature Tw. Unlike melting, sublimation and evaporation, do not have a constant temperature of phase transition. This is determined by the joint solution of the system of two equations: the kinetics of sublimation and mass balance on the destructing surface (see Sublimation). Assuming that the temperature of the surface has stabilized, i.e., it has reached the maximum value Tw,max, which depends only on flux pressure pe:
(equal to the product of (α/cp) and the enthalpy drop across the boundary layer (He – Hw), where α is the heat transfer coefficient) leads to a rise in the body’s surface temperature Tw. Unlike melting, sublimation and evaporation, do not have a constant temperature of phase transition. This is determined by the joint solution of the system of two equations: the kinetics of sublimation and mass balance on the destructing surface (see Sublimation). Assuming that the temperature of the surface has stabilized, i.e., it has reached the maximum value Tw,max, which depends only on flux pressure pe:

Then the heat balance at the destructing surface can be written as (see Ablation):

Here, 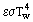 is the heated surface radiation which can be neglected at sufficiently large values of mass loss rate Gw;
is the heated surface radiation which can be neglected at sufficiently large values of mass loss rate Gw;  is the mean heat capacity of the condensed phase of the matter in the temperature range Tw up to the initial value T0; and
is the mean heat capacity of the condensed phase of the matter in the temperature range Tw up to the initial value T0; and  is the thermal effect of the injection, which can be presented as the known function of mass loss rate.
is the thermal effect of the injection, which can be presented as the known function of mass loss rate.
Consider two possible approximations of the injection effect. The first is a linear one which, strictly speaking, holds only for moderate values of mass loss rate Gw:

Substituting Eq. (2) into (1) yields

Here, γ is the injection factor γ < 1 dependent on the ratio of molecular masses of the incoming flow gas mixtures to gaseous products of evaporation; H* = c(Tw − T0) + ΔQw stands for the total quantity of heat absorbed by a unit mass of the substance while evaporating.
The second approximation of the injection effect has no upper limit for the value of injection intensity Gw:

Solving Eqs. (1) and (4) together results in

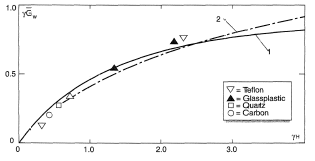
Figure 2 presents the comparative results obtained from calculating Eqs. (3) and (5). Also presented are the experimental data obtained from the destruction of Teflon (H* = 2750 kj/kg), glass-plastic with epoxide binder (H* = 12500 kj/kg), quartz-ceramics (H* = 15000 kj/kg) and graphite (H* = 34000 kj/kg) in a high-temperature air flow. Inspite of the rather large distinction between the values of H* and the known specific features of the destruction mechanisms, these results with both the prediction data and with each other.
Thus it has been shown that the injection effect becomes decisive when H > 1.5. In reality, however, the destruction mechanism of a heat protective material (evaporation, sublimation) can be complicated by a number of subsidiary effects which make it impossible to use the above relations for small and moderate values of H. To these complicating factors are attributed, first of all, the chemical reactions of separate components of the heat protective materials with each other and with the components of the incoming gas flux.
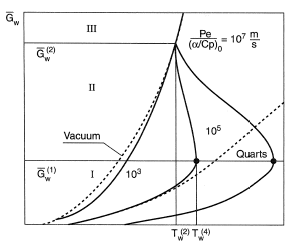
For example, Figure 3 presents a model of sublimation of glass-graphite materials in a vacuum and in air flow. The term “glass-graphite materials” covers a wide class of glass-plastics comprised of a glass-like refractory die (reinforcement) and organic binding with a large yield of coke residues (e.g., phenolformaldehyde resin). When heated up to temperatures higher than 1,000°C, this composite heat protective material transforms into a mixture of glass (SiO2) and carbon (C). There can be chemical interaction between them, both at the body surface (with a preliminary stage of sublimation of quartz glass and steam dissociation):

and also heterogeneous interaction inside the heated layer, driven by the kinetics of reaction described by the Arrhenius Equation. In any case, the carbon is efficient in capturing oxygen atoms which, according to the law of mass action, sharply increases the degree of dissociation:

This, in turn, intensifies glass evaporation nonequilibricity since it diminishes the possibility of a reverse process (condensation) taking place (see Sublimation).
At fairly small values of mass loss rate Gw, sublimation of a glass-graphite material in the air is almost the same as sublimation of a uniform quartz glass. Oxygen partial pressure p02 at the destructing surface is maintained at a sufficient level due to diffusion from the incoming flow.
An increase in the destruction rate to a certain threshold  sharply changes the oxygen mass balance. Diffusion no longer provides the required amount of oxygen, and near the surface p02 starts to drop. As a result, the degree of SiO2 molecule dissociation quickly increases, which intensifies evaporation velocity, the value of which approaches the maximum possible magnitude:
sharply changes the oxygen mass balance. Diffusion no longer provides the required amount of oxygen, and near the surface p02 starts to drop. As a result, the degree of SiO2 molecule dissociation quickly increases, which intensifies evaporation velocity, the value of which approaches the maximum possible magnitude:

In this case, the process of glass-graphite material evaporation in a dense air flow does not differ greatly from sublimation in a vacuum.
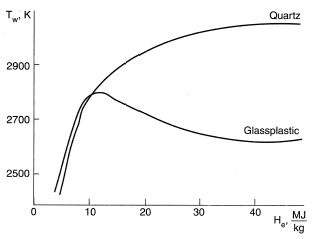
Figure 4 shows the dependence of the destructing glass-graphite material’s surface temperature Tw, on the enthalpy of the air flow He. Clearly, the difference between glass-graphite material and quartz glass runs to several hundred degrees. The presence of a viscous melt film at the destructing surface can correct the process model considered above; in particular, at the expense of decreasing me values of H* and Tw,max (see Melting).
Evaporative cooling has much in common with the systems of transpiration cooling (see Transpiration Cooling). A fundamental difference between them lies in the fact that evaporative coolant is self-regulating; i.e., the flow rate of a coolant is determined by the intensity of an external heat transfer whereas in the systems of transpiration cooling, this parameter is a priori fixed.