In the case of flow over a wedge, the velocity at the edge of the laminar boundary layer in the region of the apex can be shown to be given by, (e.g., Schlichting 1968):
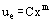
where C is a constant and the exponent is given by:

x and θ are the distance from the apex and the wedge angle, respectively, as shown in Figure 1.
For this problem, a similarity solution for the flow field can be found, if a dimensionless length, η, is introduced, defined by

where ν is the dynamic viscosity and y is the perpendicular distance from the side of the wedge. The velocity in the boundary layer can then be shown to be given by:
where u and ν are the components of velocity in the x and y directions, respectively.
f is a function of η and is defined as the solution to the Falkner-Skan equation which is:
where the primes denote differentiation with respect to η. f can be found by numerical solution of Equation (6) subject to the boundary conditions f = f' = 0 at η = 0 and f' = 1 as η → ∞.
The derivation of Equations (4), (5) and (6) can be found in, for example, White (1991), Schlichting (1968) and Brodkey (1967). The equations can also be applied to π < θ < 2π, which corresponds to a converging channel and θ = 0, in which case the equations reduce to the Blasius solution for flow over a flat plate.
REFERENCES
Brodkey, R. S. (1967) The Phenomena of Fluid Motions, Addison-Wesley Publishing Co., Reading, Massachusetts.
Schlichting, H. (1968) Boundary-Layer Theory, McGraw-Hill, New York.
White, F. M. (1991) Viscous Fluid Flow, McGraw-Hill, Inc., New York.
References
- Brodkey, R. S. (1967) The Phenomena of Fluid Motions, Addison-Wesley Publishing Co., Reading, Massachusetts.
- Schlichting, H. (1968) Boundary-Layer Theory, McGraw-Hill, New York.
- White, F. M. (1991) Viscous Fluid Flow, McGraw-Hill, Inc., New York.



