HEAT-SHIELDING PROPERTIES OF QUARTZ FIBROUS MATERIAL
Following from: The scattering problem for cylindrical particles; Radiative properties of semitransparent fibers; Near-infrared properties of quartz fibers; P1 approximation of the spherical harmonics method; Radiation of a nonisothermal layer of scattering medium
During the last decades, considerable attention has been given to investigations of the heat-shielding characteristics of fiberglass and quartz fibrous materials. One can recommend the reviews by Arduini and DePonte (1987), Viskanta and Mengç (1989), Büttner et al. (1989), Reiss (1990), Lee and Cunnington (1998, 2000), Wittwer and Platzer (2000), and Baillis and Sacadura (2000) to follow the progress in this field. The attention to this research direction is because of the widespread use of such materials and their potentials [see, for instance, Papadopoulos (2005) and Papadopoulos and Giama (2007)]. At the same time, a highly porous material of quartz fibers is just appropriate to validate the computational methods for heat transfer through polydisperse fibrous structures at the combined actions of thermal radiation and conduction. Some results of numerical and experimental studies concerning the radiative and combined heat transfer in fibrous thermal insulations can be found in Bankvall (1973), Tong and Tien (1980, 1983), Houston and Korpela (1982), Tong et al. (1983, 1989), Wang and Tien (1983), Roux et al. (1983), Lee (1986, 1988, 1989, 1993), Rish and Roux (1987), Wang et al. (1987, 2000), Stark and Fricke (1993), Jeandel et al. (1993), Dombrovsky (1994, 1996a,b), Petrov (1997), Andersen and Dyrbøl (1998), Daryabeigi (1999, 2002), Tan et al. (2000), Milandri et al. (2002), and Bai and Fan (2007). Many of the referenced papers dealt with glass or quartz fibrous materials. In more complete solutions, the heat-shielding characteristics of fibrous materials are determined by calculations based on experimental data for the disperse composition of the fibrous material and optical constants of the fiber substance. It seems to be obvious that a radiative conductivity approximation is inapplicable for semitransparent materials, and the spectral properties of the material are important for heat transfer. At the same time, the measurements of integral heat shielding parameters of highly fibrous materials remain to be an ordinary tool in the engineering practice (Litovsky et al., 1979; Daryabeigi, 1999, 2002; Marshall, 2001; Zverev et al., 2008). Therefore, a detailed study of typical radiative and combined heat transfer problems as well as an estimate of the applicability of simple physical models is of interest.
The problems of combined radiation and conduction heat transfer for semitransparent materials can be divided into two groups according to the boundary conditions. In problems of the first group, there is no thermal contact between the radiation source and the material, as in furnaces of radiative heating or in the case of solar irradiation. The boundary condition for such problems is the radiation flux. In a more general case, the convective heat transfer with an ambient medium should be taken into account. The second group of problems typical of heat-shielding materials between solid surfaces is characterized by the thermal contact with opaque radiating surfaces. In this case, the boundary condition of the first kind for the energy equation should be considered. It is obvious that combined problem statements for a semitransparent heat-shielding material on the body surface and convective or radiative heat transfer with ambient medium are widely encountered in practice.
Consider first the properties of quartz fibrous insulation in problems of the first group. The simplest variant is the radiative heating in vacuum, when the steady state solution differs slightly from that for the well-known radiative equilibrium problem (see the article Radiative equilibrium in a plane-parallel layer), and the transient solution is similar to that for the liquid droplet radiator considered in the article Liquid droplet radiator for space applications. The mathematical formulation of the 1D problem for the material layer placed between two parallel gray walls with temperatures Tw1 and Tw2 is as follows:

|
(1a) |

|
(1b) |
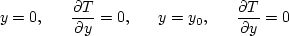
|
(1c) |

|
(1d) |
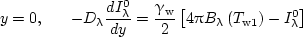
|
(1e) |

|
(1f) |
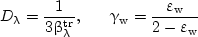
|
(1g) |
One can see that a P1 approximation is used in the above problem statement. Some numerical results for monodisperse quartz fibrous insulation of density ρ = 10 kg/m3 and thickness d = 10 mm at initial temperature T0 = 500 K and the values of εw = 0.8, Tw1 = 800 K, and Tw2 = 500 K are shown in Fig. 1. The radiative properties of randomly oriented fibers were calculated by use of the properties of single fibers at normal incidence and approximate relation (5) from the article Near-infrared properties of quartz fibers. For simplicity, the temperature dependence of the spectral optical constants was not taken into account. The parameters of the example problem considered are chosen so the optical thickness not be large. In this case, the radiative transfer throughout the entire spectrum can be calculated by numerically solving the boundary-value problem (1) from the article Radiation of a nonisothermal layer of a scattering medium.
 |
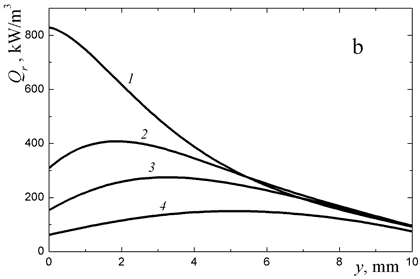 |
Figure 1. Profiles of temperature (a) and volumetric heat absorption (b) in a monodisperse layer of quartz fibers of radius a = 5 μm by radiative heating in vacuum: 1, t = 10 s, 2, 20 s, 3, 30 s,4, 50 s.
One can see in Fig. 1b that the region of maximum absorption of the radiation is displaced inward from the surface with the material heating. This effect is explained by the transparency of quartz in the shortwave range of the spectrum, i.e., for high-temperature thermal radiation.
Variation of the fiber radius from a = 2 μm to 10 μm affects considerably the heat-shielding characteristics of the material since both the absorption coefficient and transport scattering coefficient are inversely proportional to the fiber radius. In the example problem, the transfer to thinner fibers at the same density of the fibrous material reduces the transmitted heat flux by half both during the heating and in the steady thermal state (see Fig. 2). Note that the material layer thickness d and the density ρ are not separate parameters, i.e., the solution of the problem depends only on the specific surface density, which is equal to the product of ρd. The latter statement is true at negligible heat conduction through the fibers. The contribution of the heat conduction can be estimated by comparison of the steady state heat flux components qc (the conductive flux) and qr (the radiation flux) obtained by numerical solution. In the case of an isotropic material of randomly oriented quartz fibers of radius a = 5 μm, we have qc ≈ 0.07 kW/m2 and qr = 6 kW/m2 in the example problem. It goes without saying that the role of conduction increases considerably at low temperatures.
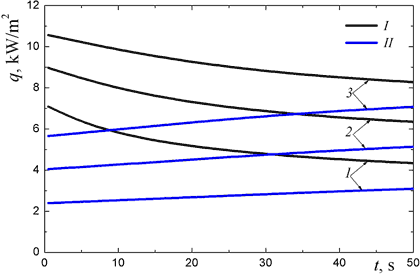 |
Figure 2. Integral radiation flux on the hot (I) and cold (II) surfaces of monodisperse fibrous layer: 1, a = 2 μm; 2, a = 5 μm; 3, a = 10 μm.
Solving the transient problem with repeated calculations of the spectral radiation transfer is very time consuming. The transfer to a simpler spectral model can cut the computational time considerably. Following the papers by Dombrovsky (1994, 1996a,b), consider the simplest two-band spectral model for the radiative properties of monodisperse quartz fibrous material,
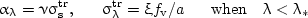
|
(2a) |
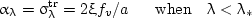
|
(2b) |
where fv = 1 - p is the volume fraction of fibers in the material. The two-band model (2) is based on a computational study of absorption and scattering of infrared radiation by quartz fibers [see the article Near-infrared properties of quartz fibers and the monograph by Dombrovsky (1996c) for further details]. The values of λ* = 6.5 μm, ξ = 0.165, and ν = 0.05 were suggested for the model parameters. The calculations showed that the heat transfer results are insensitive to small variations of λ* and ξ in the limits corresponding to different approximations of the numerical data. Conversly, the value of ν appears to be more important. One can see in Fig. 3 that the two-band model (2) with the coefficient ν = 0.05 yields sufficiently good results of heat transfer calculations.
 |
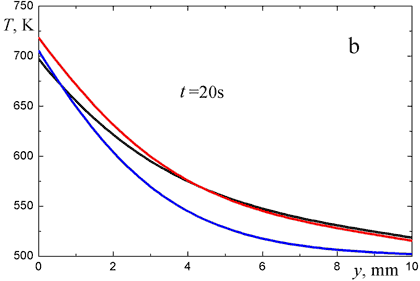 |
Figure 3. Integral radiation flux (a) on the hot (I) and cold (II) surfaces, and the temperature profiles (b) in monodisperse layer of quartz fibrous material at a = 5 μm: 1, detailed spectral calculation; 2 and 3, two-band spectral model (2, ν = 0; 3, ν = 0.05).
In the case of a considerable contribution of thermal conductivity, the solution of the problem discussed is much more complicated, even in terms of the two-band spectral model. Therefore, it is of interest to analyze some additional simplifications of the radiative transfer calculations. One can radically simplify the computational procedure by ignoring an error of the two-band model at ν = 0, i.e., by neglecting the radiation absorption in the shortwave range of λ < λ*. In this case, the diffusion approximation gives the following expression for the spectral radiation flux in this range:

|
(3) |
where the radiation diffusion coefficient Dλ and parameters γw1 and γw2 are
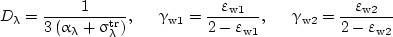
|
(4) |
As for the long-wave range of λ > λ*, one can use there the radiative conduction approximation with the radiative conductivity multiplied by the following coefficient:
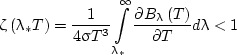
|
(5) |
This coefficient can also be expressed in the form
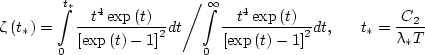
|
(6) |
where C2 = 1.438 × 10-2 m·K. At low temperatures, the value of ζ is slightly less than unity, but it decreases considerably at elevated temperatures. Note that the numerical results obtained by Eq. (6) for the temperature range from 300 to 1300 K can be approximated by the following equation (Dombrovsky, 1996c):

|
(7) |
where, as usual, T is expressed in Kelvin and λ in microns. It should be noted that the approximate model suggested differs from the Rosseland approximation, i.e., from the classic radiative conduction model, because of the other integration limits in Eq. (5), which does not include the region of the material semitransparency. A comparison of the above-described approximate model with the calculations by the complete two-band model for monodisperse quartz fibrous insulation in the case of thermal contact with the walls is presented in Fig. 4. The following values of the parameters were used in the calculations: T0 = Tw2 = 600 K, Tw1 = 700 K, εw1 = εw2 = 0.8, ρ = 10 kg/m3, ρs = 2200 kg/m3, c = 10 kJ/(kg·K), ks = 1.5 W/(m·K), and a = 5 μm. The thermal conductivity of the material in vacuum was calculated by the following formula:

|
(8) |
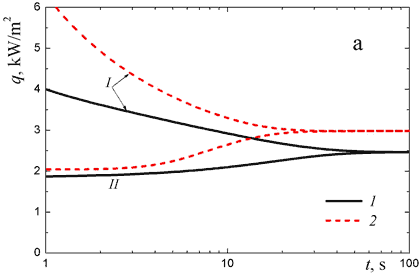
When we use the radiative conduction approximation in the range of material opacity, the heat flux on the hot surface at the process beginning appears to be incorrect (see Fig. 4), but this effect decreases at steady state. For this reason, the steady state data presented below were obtained by use of the simplified approach. Note that the computational time appears to be two orders of magnitude less than that in the detailed spectral calculations.
 |
 |
Figure 4. Total heat flux on the hot (I) and cold (II) surfaces of quartz fibrous material: (a) d = 5 mm; (b) d = 10 mm; 1, complete two-band spectral model (ν = 0.05); 2, simplified model based on radiative conduction approximation.
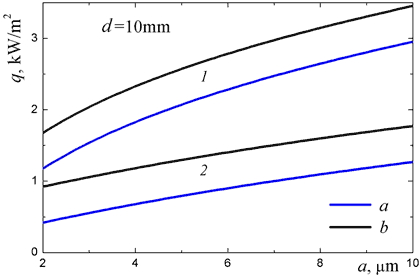
One can see in Fig. 5 that the steady state heat flux increases monotonically with the fiber radius. This effect is especially pronounced for low-density materials. In other words, the finer fibers, the better are the thermal shielding characteristics of the quartz fibrous material. Dependencies of the heat flux on the material layer thickness (see Fig. 5b) are obvious, and it is convenient to introduce the effective thermal conductivity,
 |
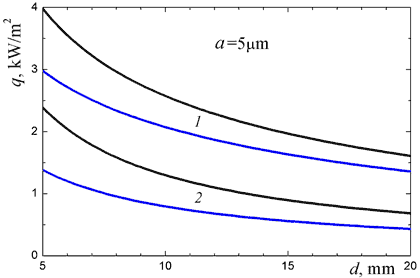 |
Figure 5. Steady state heat fluxes through the monodisperse layer of quartz fibrous insulation; dependences on the fiber radius and the layer thickness: (a) in vacuum; (b) in nitrogen at atmospheric pressure; 1, ρ = 10 kg/m3; 2, ρ = 50 kg/m3.

|
(9) |
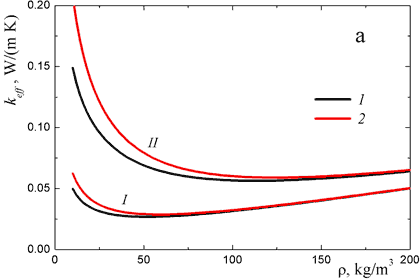
for narrow temperature intervals. Some computational results for this quantity are shown in Fig. 6. The calculations are performed at fixed values of the fiber radius a = 5 μm and the temperature difference ΔT = Tw1 - Tw2 = 100 K. The value of keff not only increases considerably with temperature, but also depends on the material density. There is also an effect of the layer thickness on the effective conductivity. At the same time, the presence of a gas in the material can be treated in this example in terms of the additive approximation (compare Figs. 6a and 6b). It is of interest that dependences keff(ρ) are nonmonotonic: there is a density of the fibrous material ρ* corresponding to the best heat shielding. In the example problem considered, the value of ρ* varies from 50 to 100 kg/m3 according to the temperature interval. The effect of the fiber radius and the temperature on ρ* can be estimated from a comparison of the thermal conductivity given by Eq. (8) and the radiative conductivity. It is easy to verify that
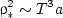
|
(10) |
 |
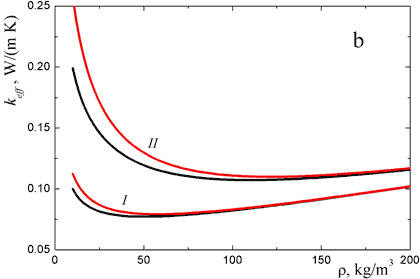 |
Figure 6. Effective thermal conductivity of monodisperse quartz fibrous insulation in vacuum (a) and in nitrogen at atmospheric pressure (b): 1, d = 5 mm; 2, d = 10 mm; I, Tw1 = 600 K and Tw2 = 400 K; II, Tw1 = 700 K and Tw2 = 600 K.
This relation was confirmed by numerical calculations. Note that the concrete value of ρ* is connected with the value of the thermal conductivity, and depends on the orientation of the fibers and on thermal contact between them. Note that the accuracy of the computational results presented in Fig. 6 is mainly determined by the uncertainty of the fibrous material conductivity rather than by the errors in radiative transfer calculations.
The concept of the effective thermal conductivity is traditionally used in engineering analysis of experimental data for heat-shielding properties of disperse materials (Dul’nev and Zarichnyak, 1974), specifically for quartz fibrous insulations (Litovsky et al., 1979; Daryabeigi, 1999, 2002; Marshall, 2001; Bai and Fan, 2007; Zverev et al., 2008; Zhang et al., 2008; Zhao et al., 2009). The above analysis showed that the values of keff, as a rule, cannot be used immediately in heat transfer calculations. At the same time, steady state heat flux measurements enable one to estimate an effective fiber radius for subsequent spectral calculations in a monodisperse approximation.
It goes without saying that the example problem considered is not general. Nevertheless, one can see that a spectral model of two bands with the different approximate descriptions of the radiative transfer in each band may be very useful. This approach is expected to be applicable to combined radiation and conduction heat transfer in quite different semitransparent scattering materials.
REFERENCES
Andersen, F. M. B. and Dyrbøl, S., Modelling Radiative Heat Transfer in Fibrous Materials: The Use of Planck Mean Properties Compared to Spectral and Flux-Weighted Properties, J. Quant. Spectrosc. Radiat. Transfer, vol. 60, no. 4, pp. 593-603, 1998.
Arduini, M. and DePonte, F., Combined Radiation and Conduction Heat Transfer in Insulating Materials, High Temp.-High. Press., vol. 19, no. 3, pp. 237-249, 1987.
Bai, D. and Fan, X.-J., On the Combined Heat Transfer in the Multilayer Non-Gray Porous Fibrous Insulation, J. Quant. Spectr. Radiat. Transfer, vol. 104, no. 3, pp. 326-341, 2007.
Baillis, D. and Sacadura, J.-F., Thermal Radiation Properties of Dispersed Media: Theoretical Prediction and Experimental Characterization, J. Quant. Spectr. Radiat. Transfer, vol. 67, no. 5, pp. 327-363, 2000.
Bankvall, C., Heat Transfer in Fibrous Materials, J. Test. Eval., vol. 1, no. 3, pp. 235-243, 1973.
Büttner, D., Kreh, A., Fricke, J., and Reiss, H., Recent Advances in Thermal Superinsulations, High Temp.-High Press., vol. 21, no. 1, pp. 39-50, 1989.
Daryabeigi, K., Analysis and Testing of High Temperature Fibrous Insulation for Reusable Launch Vehicles, AIAA Paper No. 1044, 1999.
Daryabeigi, K., Thermal Analysis and Design of Multilayer Insulation for Reentry Aerodynamic Heating, J. Spacecraft Rockets, vol. 39, no. 4, pp. 509-514, 2002.
Dombrovsky, L. A., Quartz-Fiber Thermal Insulation: Calculation of Spectral Radiation Characteristics in the Infrared Region, High Temp., vol. 32, no. 2, pp. 209-215, 1994.
Dombrovsky, L. A., Analysis of Infrared Radiation Characteristics of Isotropic Fiberglass Materials in the Semitransparency Region, High Temp., vol. 34, no. 1, pp. 156-158, 1996a.
Dombrovsky, L. A., Quartz-Fiber Thermal Insulation: Infrared Radiative Properties and Calculation of Radiative-Conductive Heat Transfer, ASME J. Heat Transfer, vol. 118, no. 2, pp. 408-414, 1996b.
Dombrovsky, L. A., Radiation Heat Transfer in Disperse Systems, Begell House, New York and Redding, CT, 1996c.
Dul’nev, G. N. and Zarichnyak, Yu. P., Thermal Conductivity of Mixtures and Composite Materials, Energiya, Leningrad, 1974 (in Russian).
Houston, R. L. and Korpela, S. A., Heat Transfer through Fiberglass Insulation, Proc. 7th Int. Heat Transfer Conf., vol. 2, Hemisphere Publ., Munich, Germany, pp. 499-504, 1982.
Jeandel, G., Boulet, P., and Morlot, G., Radiative Transfer through a Medium of Silica Fibers Oriented in Parallel Planes, Int. J. Heat Mass Transfer, vol. 36, no. 3, pp. 531-536, 1993.
Lee, S. C., Radiative Transfer through a Fibrous Medium: Allowance for Fiber Orientation, J. Quant. Spectr. Radiat. Transfer, vol. 36, no. 3, pp. 253-263, 1986.
Lee, S. C., Radiation Heat-Transfer Model for Fibers Oriented Parallel to Diffuse Boundaries, J. Thermophys. Heat Transfer, vol. 2, no. 4, pp. 303-308, 1988.
Lee, S.-C., Effect of Fiber Orientation on Thermal Radiation in Fibrous Media, Int. J. Heat Mass Transfer, vol. 32, no. 2, pp. 311-319, 1989.
Lee, S.-C., Enhanced Thermal Performance of Fibrous Insulation Containing Nonhomogeneous Fibers, J. Quant. Spectr. Radiat. Transfer, vol. 50, no. 2, pp. 199-209, 1993.
Lee, S.-C. and Cunnington, G. R., Theoretical Models for Radiative Transfer in Fibrous Media, Annual Review in Heat Transfer, C. L. Tien (ed.), vol. 9, Begell House, New York and Redding, CT, pp. 159-218, 1998.
Lee, S.-C. and Cunnington, G. R., Conduction and Radiation Heat Transfer in High-Porosity Fiber Thermal Insulation, J. Thermophys. Heat Transfer, vol. 14, no. 2, pp. 121-136, 2000.
Litovsky, E. Ya., Bondarenko, S. L., Polonsky, Yu. A., and Gashichev, N. L., An Effect of Filament Diameter on Effective Conductivity of Fireproof Thermal Insulation, High Temp., vol. 17, no. 5, pp. 997-1000, 1979 (in Russian).
Marshall, J., Internal Radiation Transport and Effective Thermal Conductivity of Fibrous Ceramic Insulations, AIAA Paper No. 2822, 2001.
Milandri, A., Asllanaj, F., Jeandel, G., and Roche, J. R., Heat Transfer by Radiation and Conduction in Fibrous Media without Axial Symmetry, J. Quant. Spectrosc. Radiat. Transfer, vol. 74, no. 5, pp. 585-603, 2002.
Papadopoulos, A. M., State of the Art in Thermal Insulation Materials and Aims for Future Developments, Energy Build., vol. 37, no. 1, pp. 77-86, 2005.
Papadopoulos, A. M. and Giama, E., Environmental Performance Evaluation of Thermal Insulation Materials and its Impact on the Buildings, Build. Environ., vol. 42, no. 5, pp. 2178-2187, 2007.
Petrov, V. A., Combined Radiation and Conduction Heat Transfer in High-Temperature Fiber Thermal Insulation, Int. J. Heat Mass Transfer, vol. 40, no. 9, pp. 2241-2247, 1997.
Reiss, H., Radiative Transfer in Nontransparent Dispersed Media, High Temp.-High Press., vol. 22, no. 5, pp. 481-522, 1990.
Rish, J. W. and Roux, J. A., Heat Transfer Analysis of Fiberglass Insulations with and without Foil Radiant Barriers, J. Thermophys. Heat Transfer, vol. 1, no. 1, pp. 43-49, 1987.
Roux, J. A., Yeh, H. Y., Smith, A. M., and Wang, S. Y., Finite Element Analysis of Radiative Transport in Fibrous Insulation, J. Energy, vol. 7, no. 6, pp. 702-709, 1983.
Stark, C. and Fricke, J., Improved Heat-Transfer Models for Fibrous Insulations, Int. J. Heat Mass Transfer, vol. 36, no. 3, pp. 617-625, 1993.
Tan, H.-P., Wang, P.-Y., and Xia, X.-L., Transient Coupled Radiation and Conduction in an Absorbing and Scattering Composite Layer, J. Thermophys. Heat Transfer, vol. 14, no. 1, pp. 77-87, 2000.
Tong, T. W. and Tien, C. L., Analytical Models for Thermal Radiation in Fibrous Insulations, J. Therm. Insul., vol. 4, no. 7, pp. 27-44, 1980.
Tong, T. W. and Tien, C. L., Radiative Heat Transfer in Fibrous Insulations--Part I: Analytical Study, ASME J. Heat Transfer, vol. 105, no. 1, pp. 70-75, 1983.
Tong, T. W., Yang, Q. S., and Tien, C. L., Radiative Heat Transfer in Fibrous Insulations - Part II: Experimental Study, ASME J. Heat Transfer, vol. 105, no. 1, pp. 76-81, 1983.
Tong, T. W., Swathi, P. S., and Cunnington, G. R., Reduction of Radiative Heat Transfer in Thermal Insulations by Use of Dielectric Coated Fibers, Int. Comm. Heat Mass Transfer, vol. 16, no. 6, pp. 851-856, 1989.
Viskanta, R. and Mengç, M. P., Radiative Transfer in Dispersed Media, Appl. Mech. Rev., vol. 42, no. 9, pp. 241-259, 1989.
Wang, K. Y. and Tien, C. L., Radiative Heat Transfer through Opacified Fibers and Powders, J. Quant. Spectrosc. Radiat. Transfer, vol. 30, no. 3, pp. 213-223, 1983.
Wang, K. Y., Kumar, S., and Tien, C. L., Radiative Transfer in Thermal Insulations of Hollow and Coated Fibers, J. Thermophys. Heat Transfer, vol. 1, no. 4, pp. 289-295, 1987.
Wang, P.-Y., Tan, H.-P., Liu, L.-H., and Tong, T. W., Coupled Radiation and Conduction in a Scattering Composite Layer with Coatings, J. Thermophys. Heat Transfer, vol. 14, no. 4, pp. 512-522, 2000.
Wittwer, V. and Platzer, W., Transparent Thermal Insulation Materials and Systems: State of the Art and Potential for the Future, High Temp.-High Press., vol. 32, no. 2, pp. 143-158, 2000.
Zhang, B.-M., Zhao, S.-Y., and He, X.-D., Experimental and Theoretical Studies on High-Temperature Thermal Properties of Fibrous Insulation, J. Quant. Spectrosc. Radiat. Transfer, vol. 109, no. 7, pp. 1309-1324, 2008.
Zhao, S.-Y., Zhang, B.-M., and He, X.-D., Temperature and Pressure Dependent Effective Thermal Conductivity of Fibrous Insulation, Int. J. Thermal Sci., vol. 48, no. 2, pp. 440-448, 2009.
Zverev, V. G., Gol’din, V. D., and Nazarenko, V. A., Radiation-Conduction Heat Transfer in Fibrous Heat-Resistant Insulation under Thermal Effect, High Temp., vol. 46, no. 1, pp. 108-114, 2008.
参考文献列表
- Andersen, F. M. B. and Dyrbøl, S., Modelling Radiative Heat Transfer in Fibrous Materials: The Use of Planck Mean Properties Compared to Spectral and Flux-Weighted Properties, J. Quant. Spectrosc. Radiat. Transfer, vol. 60, no. 4, pp. 593-603, 1998.
- Arduini, M. and DePonte, F., Combined Radiation and Conduction Heat Transfer in Insulating Materials, High Temp.-High. Press., vol. 19, no. 3, pp. 237-249, 1987.
- Bai, D. and Fan, X.-J., On the Combined Heat Transfer in the Multilayer Non-Gray Porous Fibrous Insulation, J. Quant. Spectr. Radiat. Transfer, vol. 104, no. 3, pp. 326-341, 2007.
- Baillis, D. and Sacadura, J.-F., Thermal Radiation Properties of Dispersed Media: Theoretical Prediction and Experimental Characterization, J. Quant. Spectr. Radiat. Transfer, vol. 67, no. 5, pp. 327-363, 2000.
- Bankvall, C., Heat Transfer in Fibrous Materials, J. Test. Eval., vol. 1, no. 3, pp. 235-243, 1973.
- Büttner, D., Kreh, A., Fricke, J., and Reiss, H., Recent Advances in Thermal Superinsulations, High Temp.-High Press., vol. 21, no. 1, pp. 39-50, 1989.
- Daryabeigi, K., Analysis and Testing of High Temperature Fibrous Insulation for Reusable Launch Vehicles, AIAA Paper No. 1044, 1999.
- Daryabeigi, K., Thermal Analysis and Design of Multilayer Insulation for Reentry Aerodynamic Heating, J. Spacecraft Rockets, vol. 39, no. 4, pp. 509-514, 2002.
- Dombrovsky, L. A., Quartz-Fiber Thermal Insulation: Calculation of Spectral Radiation Characteristics in the Infrared Region, High Temp., vol. 32, no. 2, pp. 209-215, 1994.
- Dombrovsky, L. A., Analysis of Infrared Radiation Characteristics of Isotropic Fiberglass Materials in the Semitransparency Region, High Temp., vol. 34, no. 1, pp. 156-158, 1996a.
- Dombrovsky, L. A., Quartz-Fiber Thermal Insulation: Infrared Radiative Properties and Calculation of Radiative-Conductive Heat Transfer, ASME J. Heat Transfer, vol. 118, no. 2, pp. 408-414, 1996b.
- Dombrovsky, L. A., Radiation Heat Transfer in Disperse Systems, Begell House, New York and Redding, CT, 1996c.
- Dul’nev, G. N. and Zarichnyak, Yu. P., Thermal Conductivity of Mixtures and Composite Materials, Energiya, Leningrad, 1974 (in Russian).
- Houston, R. L. and Korpela, S. A., Heat Transfer through Fiberglass Insulation, Proc. 7th Int. Heat Transfer Conf., vol. 2, Hemisphere Publ., Munich, Germany, pp. 499-504, 1982.
- Jeandel, G., Boulet, P., and Morlot, G., Radiative Transfer through a Medium of Silica Fibers Oriented in Parallel Planes, Int. J. Heat Mass Transfer, vol. 36, no. 3, pp. 531-536, 1993.
- Lee, S. C., Radiative Transfer through a Fibrous Medium: Allowance for Fiber Orientation, J. Quant. Spectr. Radiat. Transfer, vol. 36, no. 3, pp. 253-263, 1986.
- Lee, S. C., Radiation Heat-Transfer Model for Fibers Oriented Parallel to Diffuse Boundaries, J. Thermophys. Heat Transfer, vol. 2, no. 4, pp. 303-308, 1988.
- Lee, S.-C., Effect of Fiber Orientation on Thermal Radiation in Fibrous Media, Int. J. Heat Mass Transfer, vol. 32, no. 2, pp. 311-319, 1989.
- Lee, S.-C., Enhanced Thermal Performance of Fibrous Insulation Containing Nonhomogeneous Fibers, J. Quant. Spectr. Radiat. Transfer, vol. 50, no. 2, pp. 199-209, 1993.
- Lee, S.-C. and Cunnington, G. R., Theoretical Models for Radiative Transfer in Fibrous Media, Annual Review in Heat Transfer, C. L. Tien (ed.), vol. 9, Begell House, New York and Redding, CT, pp. 159-218, 1998.
- Lee, S.-C. and Cunnington, G. R., Conduction and Radiation Heat Transfer in High-Porosity Fiber Thermal Insulation, J. Thermophys. Heat Transfer, vol. 14, no. 2, pp. 121-136, 2000.
- Litovsky, E. Ya., Bondarenko, S. L., Polonsky, Yu. A., and Gashichev, N. L., An Effect of Filament Diameter on Effective Conductivity of Fireproof Thermal Insulation, High Temp., vol. 17, no. 5, pp. 997-1000, 1979 (in Russian).
- Marshall, J., Internal Radiation Transport and Effective Thermal Conductivity of Fibrous Ceramic Insulations, AIAA Paper No. 2822, 2001.
- Milandri, A., Asllanaj, F., Jeandel, G., and Roche, J. R., Heat Transfer by Radiation and Conduction in Fibrous Media without Axial Symmetry, J. Quant. Spectrosc. Radiat. Transfer, vol. 74, no. 5, pp. 585-603, 2002.
- Papadopoulos, A. M., State of the Art in Thermal Insulation Materials and Aims for Future Developments, Energy Build., vol. 37, no. 1, pp. 77-86, 2005.
- Papadopoulos, A. M. and Giama, E., Environmental Performance Evaluation of Thermal Insulation Materials and its Impact on the Buildings, Build. Environ., vol. 42, no. 5, pp. 2178-2187, 2007.
- Petrov, V. A., Combined Radiation and Conduction Heat Transfer in High-Temperature Fiber Thermal Insulation, Int. J. Heat Mass Transfer, vol. 40, no. 9, pp. 2241-2247, 1997.
- Reiss, H., Radiative Transfer in Nontransparent Dispersed Media, High Temp.-High Press., vol. 22, no. 5, pp. 481-522, 1990.
- Rish, J. W. and Roux, J. A., Heat Transfer Analysis of Fiberglass Insulations with and without Foil Radiant Barriers, J. Thermophys. Heat Transfer, vol. 1, no. 1, pp. 43-49, 1987.
- Roux, J. A., Yeh, H. Y., Smith, A. M., and Wang, S. Y., Finite Element Analysis of Radiative Transport in Fibrous Insulation, J. Energy, vol. 7, no. 6, pp. 702-709, 1983.
- Stark, C. and Fricke, J., Improved Heat-Transfer Models for Fibrous Insulations, Int. J. Heat Mass Transfer, vol. 36, no. 3, pp. 617-625, 1993.
- Tan, H.-P., Wang, P.-Y., and Xia, X.-L., Transient Coupled Radiation and Conduction in an Absorbing and Scattering Composite Layer, J. Thermophys. Heat Transfer, vol. 14, no. 1, pp. 77-87, 2000.
- Tong, T. W. and Tien, C. L., Analytical Models for Thermal Radiation in Fibrous Insulations, J. Therm. Insul., vol. 4, no. 7, pp. 27-44, 1980.
- Tong, T. W. and Tien, C. L., Radiative Heat Transfer in Fibrous Insulations--Part I: Analytical Study, ASME J. Heat Transfer, vol. 105, no. 1, pp. 70-75, 1983.
- Tong, T. W., Yang, Q. S., and Tien, C. L., Radiative Heat Transfer in Fibrous Insulations - Part II: Experimental Study, ASME J. Heat Transfer, vol. 105, no. 1, pp. 76-81, 1983.
- Tong, T. W., Swathi, P. S., and Cunnington, G. R., Reduction of Radiative Heat Transfer in Thermal Insulations by Use of Dielectric Coated Fibers, Int. Comm. Heat Mass Transfer, vol. 16, no. 6, pp. 851-856, 1989.
- Viskanta, R. and Mengç, M. P., Radiative Transfer in Dispersed Media, Appl. Mech. Rev., vol. 42, no. 9, pp. 241-259, 1989.
- Wang, K. Y. and Tien, C. L., Radiative Heat Transfer through Opacified Fibers and Powders, J. Quant. Spectrosc. Radiat. Transfer, vol. 30, no. 3, pp. 213-223, 1983.
- Wang, K. Y., Kumar, S., and Tien, C. L., Radiative Transfer in Thermal Insulations of Hollow and Coated Fibers, J. Thermophys. Heat Transfer, vol. 1, no. 4, pp. 289-295, 1987.
- Wang, P.-Y., Tan, H.-P., Liu, L.-H., and Tong, T. W., Coupled Radiation and Conduction in a Scattering Composite Layer with Coatings, J. Thermophys. Heat Transfer, vol. 14, no. 4, pp. 512-522, 2000.
- Wittwer, V. and Platzer, W., Transparent Thermal Insulation Materials and Systems: State of the Art and Potential for the Future, High Temp.-High Press., vol. 32, no. 2, pp. 143-158, 2000.
- Zhang, B.-M., Zhao, S.-Y., and He, X.-D., Experimental and Theoretical Studies on High-Temperature Thermal Properties of Fibrous Insulation, J. Quant. Spectrosc. Radiat. Transfer, vol. 109, no. 7, pp. 1309-1324, 2008.
- Zhao, S.-Y., Zhang, B.-M., and He, X.-D., Temperature and Pressure Dependent Effective Thermal Conductivity of Fibrous Insulation, Int. J. Thermal Sci., vol. 48, no. 2, pp. 440-448, 2009.
- Zverev, V. G., Gol’din, V. D., and Nazarenko, V. A., Radiation-Conduction Heat Transfer in Fibrous Heat-Resistant Insulation under Thermal Effect, High Temp., vol. 46, no. 1, pp. 108-114, 2008.