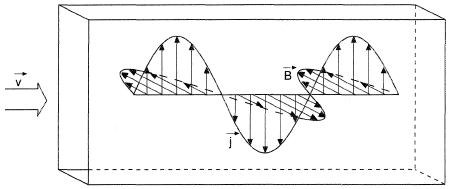
MHD generators (MHD electrical power generators) are devices in which, according to the magnetohydrodynamics laws, a conversion of the energy of working fluid into electrical energy takes place. The principle of operation of MHD generators as well as conventional electrical generators is based on Faraday's induction law. In an electrically conducting fluid, moving at velocity
 in a magnetic field
in a magnetic field
 , an electromotive force (
, an electromotive force (
 ×
×
 ) is induced. When electrodes connected to an external circuit are arranged to be flowed over by the fluid, electrical current of density
) is induced. When electrodes connected to an external circuit are arranged to be flowed over by the fluid, electrical current of density
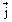 is produced by the electromotive force the current being limited by Ohm's law. Figure 1 shows a schematic diagram of an MHD generator channel, constructed from electrode and insulation walls. In the channel, the fluid works against the electromagnetic body force (
is produced by the electromotive force the current being limited by Ohm's law. Figure 1 shows a schematic diagram of an MHD generator channel, constructed from electrode and insulation walls. In the channel, the fluid works against the electromagnetic body force (
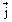 ×
×
 ). A part of this work is used for electrical energy generation in the external circuit (load). Unlike a conventional turbogenerator, the MHD generator has no moving parts and this permits one to increase substantially the working fluid temperature.
). A part of this work is used for electrical energy generation in the external circuit (load). Unlike a conventional turbogenerator, the MHD generator has no moving parts and this permits one to increase substantially the working fluid temperature.
The possibility of electrical current generation by a fluid moving in magnetic field was first pointed out by M. Faraday (1832). He made an attempt to measure electrical current induced by flow sea water in the river Thames estuary in the Earth's magnetic field. During the next century, various proposals on MHD energy conversion devices have emerged. The first experiments on electrical energy generation were performed by B. Karlovitz at the Westing-house laboratory, U.S. (1938) using an MHD generator working with nonequilibrium plasma. At the Avco-Everette laboratory, U.S. the first highpowered MHD generator Mark-V worked on combustion products of liquid fuel and oxygen. The U — 25 MHD pilot plant using natural gas fuel was commissioned at the Institute of High Temperatures, U.S.S.R. (1971). A coal-fired MHD pilot plant (CDIF) was constructed in the U.S. (1984). In the U.S.S.R., a series of pulsed MHD generators (Pamir) with solid rocket fuel were developed for earthquake predictions and mineral deposits prospecting at the Kurchatov Atomic Energy Institute and other institutions (1973-1977). The pulsed MHD generator Khibiny (1976) was designed for geophysical research and used for feeding a huge current loop in sea water around the Rybachy peninsula in the Barenz Sea.
MHD electrical power generators have prospective uses in advanced high temperature energy production cycles and high energy pulsed electrical sources.
Depending upon the kind of working fluid, the following types of MHD generators are distinguished: open cycle MHD generators operated on combustion products of various fuels; closed cycle MHD generators working on noble gases, and liquid metal MHD generators.
According to the character of electrical field variation, MHD generators are divided into conduction and induction types. In the conduction type, the MHD generator electrical field is potential (
 = -grad φ) and electrical current generated in the working fluid flows through a load (see Figure 1). In this type of MHD generator the electrodes should be arranged as shown in this figure. Conduction MHD generators can generate direct current or alternating current. In the induction type, the MHD generator's electrical field is excited by a transient magnetic field (rot
= -grad φ) and electrical current generated in the working fluid flows through a load (see Figure 1). In this type of MHD generator the electrodes should be arranged as shown in this figure. Conduction MHD generators can generate direct current or alternating current. In the induction type, the MHD generator's electrical field is excited by a transient magnetic field (rot
 = −
= −
 ) and the generated current can be short-circuited inside the working fluid. The magnetic field production the induction MHD generators can be of traveling magnetic field or transformer type. Figure 2 is a schematic diagram of an MHD generator channel with a traveling magnetic field created by external conductors. There are many alternative geometrical configurations for MHD generator channels. In Figures 1 and 2, linear channels are shown in which working fluid flows in a rectilinear pattern. A rectilinear flow can occur also in coaxial and disk channels. A curvilinear flow takes place in a vortex MHD generator with a disk or coaxial channel and in helical and spiral MHD generators.
) and the generated current can be short-circuited inside the working fluid. The magnetic field production the induction MHD generators can be of traveling magnetic field or transformer type. Figure 2 is a schematic diagram of an MHD generator channel with a traveling magnetic field created by external conductors. There are many alternative geometrical configurations for MHD generator channels. In Figures 1 and 2, linear channels are shown in which working fluid flows in a rectilinear pattern. A rectilinear flow can occur also in coaxial and disk channels. A curvilinear flow takes place in a vortex MHD generator with a disk or coaxial channel and in helical and spiral MHD generators.
The basic electrical characteristics of MHD generators are power output
 , which is generated in working fluid volume, and local electrical efficiency η, defined as a ratio of electrical power output density
, which is generated in working fluid volume, and local electrical efficiency η, defined as a ratio of electrical power output density
 to electromagnetic body force power density (
to electromagnetic body force power density (
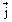 ×
×
 )·
)·
 (
(
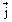 ×
×
 )·
)·
 . In MHD generators, the values of
. In MHD generators, the values of
 and (
and (
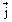 ×
×
 )·
)·
 are negative.
are negative.
Thermodynamic characteristics include enthalpy extraction coefficient ηN, which is determined as a ratio of the power output
 to the inlet stagnation enthalpy flux, ηN =
to the inlet stagnation enthalpy flux, ηN =
 /
/
 , and isoentropic efficiency η0i, defined as a ratio of the power output
, and isoentropic efficiency η0i, defined as a ratio of the power output
 to the difference of inlet and outlet stagnation enthalpies fluxes in the isoentropic expansion at given stagnation pressure ratio, η0i =
to the difference of inlet and outlet stagnation enthalpies fluxes in the isoentropic expansion at given stagnation pressure ratio, η0i =
 /
/
 . At any point in the energy conversion process, local isoentropic efficiency is determined as η0 = dW
. At any point in the energy conversion process, local isoentropic efficiency is determined as η0 = dW
 (dH0)is.
(dH0)is.
The values of η0 and η are interconnected by relationship following from conservation equations. When wall friction and heat losses are negligible, this reduces to:

This formula reflects the influence, of Joule dissipation upon η0, which increases with decreasing gas static temperature.
The relation between local electrical characteristics and flow parameters in MHD generators is governed by Ohm's law. In a linear conduction MHD generator, in which the flow velocity is directed along x-axis (
 =
=
 ) and magnetic field is directed along z-axis, the components of the Ohm's law are written as
) and magnetic field is directed along z-axis, the components of the Ohm's law are written as

where σ is the electrical conductivity of working fluid and β is the Hall coefficient. In an MHD channel of rectangular cross section with uniform flow, the z-component of current density equals zero (jz = 0). In this case the electrical power density
 is represented as
is represented as
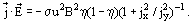
In this relationship, variables η and jx/jy are determined by the electrical scheme and load regime of MHD generator. The maximum power density is achieved when η = 0.5, jx/jy = 0, B = Bmax, and Ma = Maopt. The optimum Mach number arises from the nonmonotic dependence of the product σu2 on velocity at fixed stagnation gas parameters. The maximum value σu2 occurs at the following condition
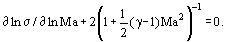
It follows from this condition that optimum flow is subsonic (Maopt < 1) for atomic gases, and supersonic (Maopt > 1) for molecular gases. For MHD generators designed for power plants, optimum Mach number Maopt has to be determined from the conditional maximum of σu2η(1 - η) at a fixed value of η0 = η0 (Ma, η).
The dependence of electrical conductivity s upon the working gas parameters is governed by the ionization of atoms and molecules and the movement of charged particles relative to neutrals. To increase the electrical conductivity, a small seeding flow of alkali metals (K, Cs, etc.) with low ionization potential is added to the gaseous working fluid. The electrical conductivity of sufficiently dense gases is determined by electron density ne and mobility μe, σ = neeμe = nee2/meτ, where e and me are election charge and mass, τ is mean time of electron-neutral collisions. The electron mobility enters in the definition of the Hall coefficient, β = μeB.
At low degrees of ionization, when neutral particles provide major part of the effective cross section for electron collision, the electrical conductivity is an exponential function of gas temperature. Such a strong dependence of electrical conductivity on temperature limits lower working temperature in MHD generator. The minimum useable outlet temperature of molecular gases is approximately equal to 2000 K. When noble gases are used in closed cycle MHD generator, it is possible to substantially decrease minimum working temperature due to nonequilibrium ionization.
In an MHD generator with nonequilibrium plasma the enhanced degree of ionization is sustained by the Joulean heating. The electrical conductivity depends on the electron temperature. To heat electrons it is necessary to have high values of the Hall coefficient (β ≥ 3). However, at the condition β > 1, ionization instability emerges in the plasma. As the magnetic field increases, the plasma transfers to the state of ionization turbulence. One of the means of stabilization of turbulent plasma is the use of flow regimes with full ionization of alkali seeding. This approach is successfully realized in disk MHD generators with nonequilibrium plasma.
Electrical conductivity of liquid metals is practically constant and large enough for utilization of the induction scheme for an MHD generator. In induction MHD generators the main losses are caused by wall friction and eddy currents induced in electrodeless channels.
The most advanced and technically feasible MHD generators (in terms of research and development) are those of the conduction type using gaseous working fluids. The presence of the Hall effect leads to a variety of electrical schemes for such MHD generators, of which are described in what follows.
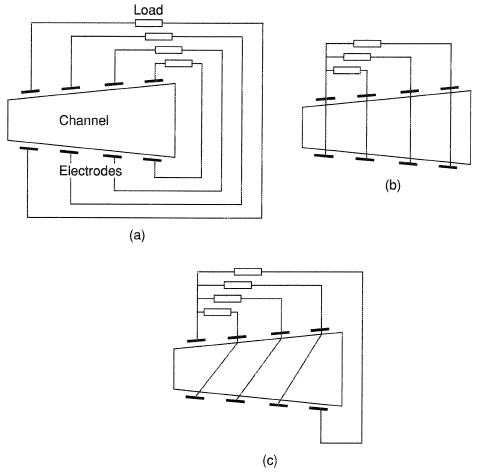
The Faraday MHD generator is characterized by an electrical scheme in which the load is supplied by the current flowing in the channel in the direction of induced electromotive force (along y-axis in Figure 1). At finite values of Hall coefficient (β ≥ 1) the electrodes of Faraday MHD generator are segmented and switched to individual loads (see Figure 3a). The electrode segmentation prevents circulation of the longitudinal current in the electrodes and plasma (jx = 0) and provides the establishment of an axial electrical field (Ex < 0). In a segmented MHD channel the power output and efficiency reach their maximum values. At small values of Hall coefficient (β < 1) the segmentation is not needed and their continuous electrodes switched to a single load are used. In a channel with continuous electrodes, the conditions Ex = 0 and jx > 0 are realized. For an ideal Faraday MHD generator (infinitely fine segmentation or absence of Hall effect) the electrical characteristics are the following
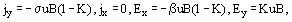
where K is the load parameter, determined by the external circuit. In a Hall MHD generator the axial current jx is supplied to the load, which is switched to the sections of segmented channel (see Figure 3b). In each section the opposite electrodes are shorted (Ey = 0). The power output of Hall generator is lower than that of Faraday channel at the same efficiency. The characteristics of the Hall channel reach the ideal segmented Faraday channel values when β → ∞.
The series MHD generator has a prescribed direction of the electrical field vector in the channel. The ratio of the electrical field vector components defines the angle α between the equipotential lines and the axis of the channel

This condition is provided by shorting of the electrodes of the segmented channel along the equipotential lines (see Figure 3c). The load current of series channel contains both components of electrical current jx and jy. A series channel is transformed to a Hall channel at α = π/2. Both Hall and series channels can operate with a single load switched to inlet and outlet of the channel. For any regime of operation of the Faraday channel it is possible to configurate series channel having the same electrical characteristics by matching the equipotential angle α to the condition jx = 0. But at the off-design conditions the characteristics of series channel with fixed a are worse than those of the Faraday channel.
Distributions of flow parameters over the channel cross section are nonuniform owing to skin friction and heat transfer at the walls. Major effects influencing electrical current flow in MHD channel are revealed when the equations of Ohm's law are averaged over the cross section. The Ohm’s law equations can be averaged if a certain model distribution of electrical parameters is assumed. In the case of the parallel equipotentials model, when the following assumptions are introduced


the averaged components of Ohm's law can be expressed as


here, double brackets denote averaging along both axes in the channel cross section,
 Jy
Jy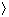 y does not depend on y because the normal component of current density at the insulator side wall is equal to zero,
y does not depend on y because the normal component of current density at the insulator side wall is equal to zero,
 Ey
Ey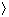 y does not depend on z because electrodes are assumed to be ideal conductors; the coefficients G and α are defined as
y does not depend on z because electrodes are assumed to be ideal conductors; the coefficients G and α are defined as
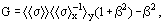
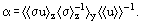
G-factor reflects the two most important effects in a MHD channel with nonuniform flow, i.e., the Ohmic resistance of the electrode layers and the circulation of the Hall current which flows in a negative direction with respect to the x-axis in the core, where electrical conductivity is higher than the mean value, and in a positive direction with respect to the x-axis in the electrode layers. The latter effect is enhanced when the Hall coefficient increases. To suppress this effect, a curvilinear configuration of electrodes is used. At the surface of such electrodes the z-component of electrical current, which does not induce Hall, electromotive force is substantial.
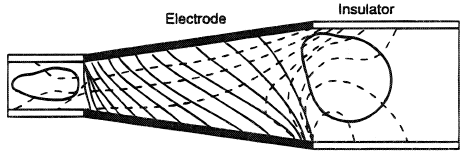
The other reason for Hall current circulation in the channel is shorting of the axial electrical field Ex by components of construction. For example, in a channel with continuous electrodes the condition Ex 0 is imposed and in the plasma, a volume axial current is induced jx ~ βjy. In Figure 4, current stream lines (solid curves) and equipotential lines (broken lines) in continuous electrode channel are drawn for β ≈ 1. Losses caused by Hall current lead to power output decreases by approximately 1 +
0 is imposed and in the plasma, a volume axial current is induced jx ~ βjy. In Figure 4, current stream lines (solid curves) and equipotential lines (broken lines) in continuous electrode channel are drawn for β ≈ 1. Losses caused by Hall current lead to power output decreases by approximately 1 +
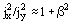 times. Segmentation of electrodes allows an axial electrical field to be sustained of finite value Ex. At small ratio of electrode pitch Δl to distance between opposite electrodes Y (Δl/Y << 1) the condition jx ≈ 0 is fulfilled. However, at the surface of individual electrode, the Hall effect causes asymmetrical distribution of current density. When Hall coefficient β increases, the current concentrations at the electrode edges (upstream for the anode and downstream for the cathode) grow rapidly.
times. Segmentation of electrodes allows an axial electrical field to be sustained of finite value Ex. At small ratio of electrode pitch Δl to distance between opposite electrodes Y (Δl/Y << 1) the condition jx ≈ 0 is fulfilled. However, at the surface of individual electrode, the Hall effect causes asymmetrical distribution of current density. When Hall coefficient β increases, the current concentrations at the electrode edges (upstream for the anode and downstream for the cathode) grow rapidly.
Nonuniform distribution of magnetic field can also be the cause of a short-circuited current in the channel. Usually the greatest nonuniformities of magnetic field occur at the inlet and the outlet of the channel. At nonuniform magnetic field distribution B(x) a variable electromotive force (
 ×
×
 ) is induced which can produce current loops in the plasma volume. In Figure 4 one can see the current loops in the end regions of the channel, where an exponential decrease of magnetic field is arranged. One of the ways of reducing the short-circuited current is through the loading of the end regions of the channel by means of segmented electrodes according to the variation of (
) is induced which can produce current loops in the plasma volume. In Figure 4 one can see the current loops in the end regions of the channel, where an exponential decrease of magnetic field is arranged. One of the ways of reducing the short-circuited current is through the loading of the end regions of the channel by means of segmented electrodes according to the variation of (
 ×
×
 ) along the x-axis.
) along the x-axis.
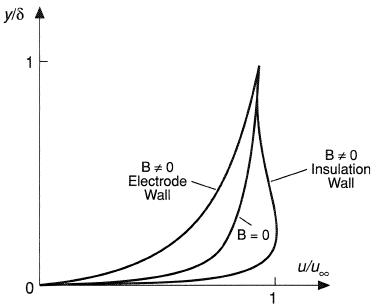
Magnetohydrodynamic interaction produces the additional nonuniformities of working fluid parameters in the flow. At the electrode wall, the electromagnetic body force (
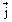 ×
×
 )x, which decelerates the flow, causes the deformation of the velocity profile in the boundary layer. Since the variation of (
)x, which decelerates the flow, causes the deformation of the velocity profile in the boundary layer. Since the variation of (
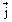 ×
×
 )x across the boundary layer is relatively small, the velocity profile at the electrode wall becomes less steep. In an MHD channel with strong deceleration of the flow, boundary layer separation can occur. To prevent the boundary layer separation it is necessary to control the rate of deceleration of the MHD flow. At the insulation walls, where the electromagnetic body force (
)x across the boundary layer is relatively small, the velocity profile at the electrode wall becomes less steep. In an MHD channel with strong deceleration of the flow, boundary layer separation can occur. To prevent the boundary layer separation it is necessary to control the rate of deceleration of the MHD flow. At the insulation walls, where the electromagnetic body force (
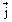 ×
×
 )x is nonuniform, the opposite effect (Hartman effect) takes place. In Figure 4 the deformation of the velocity profile is shown. Joulean heating flattens the temperature profile in the boundary layer and increases heat flux to the channel wall. When the transverse component of electromagnetic body force (
)x is nonuniform, the opposite effect (Hartman effect) takes place. In Figure 4 the deformation of the velocity profile is shown. Joulean heating flattens the temperature profile in the boundary layer and increases heat flux to the channel wall. When the transverse component of electromagnetic body force (
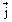 ×
×
 )y is substantial in an MHD channel, a secondary flow is generated. The secondary flow causes a nonuniform distribution of plasma parameters along the perimeter of the channel cross section and redistribution of electrical field and current at the channel walls.
)y is substantial in an MHD channel, a secondary flow is generated. The secondary flow causes a nonuniform distribution of plasma parameters along the perimeter of the channel cross section and redistribution of electrical field and current at the channel walls.
The principal influence upon the characteristics and reliability of the MHD generator is exerted by the regime of current discharge at the electrode surface. There are three main regimes of discharge: diffuse mode, microarcing and high current arcing. The existing theoretical and experimental data show that the transition from one mode of discharge to another one is determined by current density and thermal conditions at the electrode surface. In an open cycle, MHD generator the diffuse mode of discharge occurs at Tw ≥ 2000 K and j ≤ 104 A/m2. At lower electrode temperature, arcing arises. Nonlinear arc phenomena result in nonuniform current and potential distribution at the electrodes and in interelectrode breakdown. The interelectrode arcs are affected by the transversal electromagnetic force (
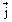 ×
×
 )y. When the force (
)y. When the force (
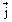 ×
×
 )y moves the arc into the interelectrode insulator, the ceramic material of insulator is locally overheated and can be destroyed. This mechanism is the one which is mainly responsible for failure of MHD channel constructions. In order to avoid the interelectrode breakdown, devices for current control in the electrodes circuits are used.
)y moves the arc into the interelectrode insulator, the ceramic material of insulator is locally overheated and can be destroyed. This mechanism is the one which is mainly responsible for failure of MHD channel constructions. In order to avoid the interelectrode breakdown, devices for current control in the electrodes circuits are used.
Mathematical modeling of flow in MHD channel is based on the equations of magnetohydrodynamics. A simple level of description of MHD flow is quasi-one-dimensional approximation, which employs the averaged equations of conservation and Ohm's law and takes into account all major effects influencing axial distribution of gasdynamic and electrodynamic parameters as well as integral characteristics of MHD generator. The quasi-one-dimensional equations are easily corrected with respect to experimental data and quite suitable to optimization procedures. In order to determine the optimal flow three variables B(x), η(x) and Ma(x) are varied along the channel. For accurate description of space structure of flow and conditions at the channel wails, the 2D and 3D MHD equations are solved, mainly by various numerical techniques.
REFERENCES
Rosa, R. J. (1968) Magnetohydrodynamic Energy Conversion, McGraw-Hill. New York.
Vatazhin, A. B., Lyubimov, G. A. and Regirer, S. A. (1970) Magnetohydrodynamic Flows in Channels. Nauka, Moscow (in Russian).
Patrick, M. and Shumyatsky, B. Ya., Eds. (1979) Open-Cycle Magnetohydrodynamic Electrical Power Generation. A Joint Publication U.S. A./U.S .S ,R., Argonne National Laboratory, Argonne, IL., USA.
Использованная литература
- Rosa, R. J. (1968) Magnetohydrodynamic Energy Conversion, McGraw-Hill. New York.
- Vatazhin, A. B., Lyubimov, G. A. and Regirer, S. A. (1970) Magnetohydrodynamic Flows in Channels. Nauka, Moscow (in Russian).
- Patrick, M. and Shumyatsky, B. Ya., Eds. (1979) Open-Cycle Magnetohydrodynamic Electrical Power Generation. A Joint Publication U.S. A./U.S .S ,R., Argonne National Laboratory, Argonne, IL., USA.