At low gas velocities, it is possible for counter current two-phase flow to occur with the gas going upwards, and the liquid falling as a film on the channel wall. At the other extreme, when the gas velocity is high, the liquid flows upwards in the film, and we have Annular Flow. The transition between these two extreme cases is illustrated in Figure 1. As the gas flow is increased, the system passes from one of falling film flow (a) through the "flooding" transition ( ) at which liquid begins to travel upwards (b), to simultaneous upward and downward flow (c and d), to climbing film flow (e). When the gas flow is now reduced, a point is reached at which liquid begins to creep below the injection point, and this is termed "flow reversal". The flooding transition is extremely important in reflux condensation, in falling film mass transfer equipment and in many aspects of reactor safety. Flooding is also important in governing the transition between Plug Flow and Churn Flow (see Gas-Liquid Flow).
) at which liquid begins to travel upwards (b), to simultaneous upward and downward flow (c and d), to climbing film flow (e). When the gas flow is now reduced, a point is reached at which liquid begins to creep below the injection point, and this is termed "flow reversal". The flooding transition is extremely important in reflux condensation, in falling film mass transfer equipment and in many aspects of reactor safety. Flooding is also important in governing the transition between Plug Flow and Churn Flow (see Gas-Liquid Flow).
The onset of flooding is extremely sensitive to the entrance geometry. This is illustrated by the results shown in Figure 2.
Obviously, the liquid and gas must be separated in some way at the bottom of the channel. If this is done smoothly through a porous wall tube section, then the flooding gas velocities are relatively high and depend on tube length, as shown. If, on the other hand, the liquid exits through a sharp-ended tube (as illustrated in Figure 2), then the flooding phenomenon is governed by the exit zone and is not dependent on tube length; furthermore, the flooding velocity is significantly lower than that obtained with smooth entrance and exit. These results are further illustrated by more recent data obtained by Govan et al. (1991) and shown in Figure 3, which show that, even with a taped (bell-mouthed) exit for the liquid, the data are significantly below those for porous wall sections.
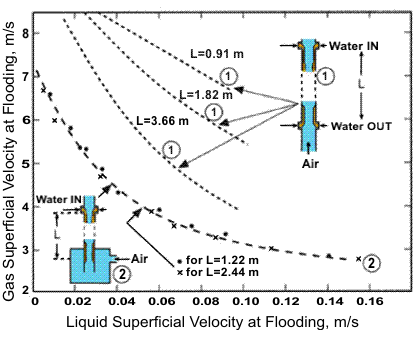
Figure 2. Flooding data for air-water flow in vertical tubes showing effect of entrance conditions (Hewitt, 1982).
In Figure 3, the data are plotted in the non-dimensional parameters:


where UG and UL are the superficial velocities of the gas and liquid phases, ρG and ρL their densities, g the acceleration due to gravity and D the tube diameter.
The most widely used correlation for flooding is that due to Wallis (1961), which is as follows:

For sharp-edged entry (see Figure 2), values of m = 1 and C = 0.75 appear to fit the data. For smooth inlet and outlet conditions, where there is an influence of tube length of flooding velocity, Jayanti and Hewitt (1992) fitted the data with C = 1 and m given by:
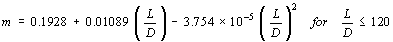

where L is the distance between the liquid inlet and the liquid outlet.
There is a general consensus that flooding is caused by the formation of large waves on the interface. Very often, the precise mechanism is clouded by entrance effects. Thus, if a vena contracta is formed at the inlet for the gas phase, this generates a low pressure zone which can lead to the creation of a spurious wave. This is the probable reason why non-smooth inlets and outlets give such different results to those obtained with smooth conditions. However, in the case of a smooth inlet and outlet (see Figure 2), then it seems that, for smaller diameter tubes at least (i.e., tubes less than approximately 5 cm in diameter), the flooding mechanism is one in which a coherent large wave is formed at the liquid outlet; this wave is then swept up the tube to beyond the inlet, this process leading to the onset of Churn Flow above the injector. For larger diameter tubes, there is some evidence that the large waves formed are not coherent, and that entrainment of the wave tips (giving rise to droplet transport) occurs before the waves, themselves are transported, and that this gives rise to upwards transport of liquid in the form of droplets which deposit above the injector position. For larger-diameter tubes, it seems probable that an alternative correlation for flooding velocity may be more appropriate. This is due to Pushkina and Sorokin (1969) and is in terms of the Kutateladze number K as follows:
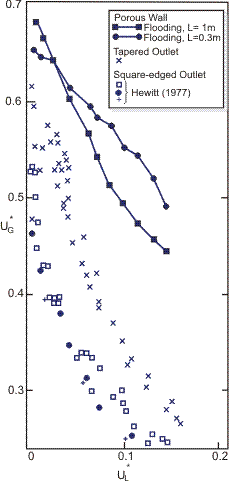
Figure 3. Comparisons of flooding data for sharp-edged, bell-mouthed (taped) and porous wall liquid exit (Govan et al., 1991).
The flow reversal transition has been formed to be relatively insensitive to liquid flow rate, and to occur at an approximately constant gas superficial velocity. For smaller diameter tubes, the flow reversal transition is correlated approximately by the expression:

and for tube diameters greater than about 5 cm. Equation (6) may be used for both flow reversal and flooding.
REFERENCES
Govan, A. H., Hewitt, G. P., Richter, H. J. and Scott, A. (1991) Flooding and churm flow in vertical pipes, Int. J. Multiphase Flow, 17: 27-44. DOI: 10.1016/0301-9322(91)90068-E
Hewitt, G. F. Flow Regimes. Chapter 2.1 of Handbook of Multiphase Systems, G. Hetsroni ed., McGraw-Hill Book Company, New York, ISBN 0-07-028460-1.
Jayanti, S. and Hewitt, G. F. (1992) Prediction of the slug-to-churn flow transition in vertical two-phase flow, Int. J. Multiphase Flow, 18: 847-860. DOI: 10.1016/0301-9322(92)90063-M
Pushkina, O. L. and Sorokin, Y. L. (1969) Breakdown of liquid film motion in vertical tubes, Heat Transfer Sov. Res., 1, 56-64.
Wallis, G. B. (1961) Flooding velocities for air and water vertical tubes. UKAA Report, AEEW-R123.
Использованная литература
- Govan, A. H., Hewitt, G. F., Richter, H. J. and Scott, A. (1991) Flooding and churm flow in vertical pipes, Int. J. Multiphase Flow, 17: 27-44. DOI: 10.1016/0301-9322(91)90068-E
- Hewitt, G. F. Flow Regimes. Chapter 2.1 of Handbook of Multiphase Systems, G. Hetsroni ed., McGraw-Hill Book Company, New York, ISBN 0-07-028460-1.
- Jayanti, S. and Hewitt, G. F. (1992) Prediction of the slug-to-churn flow transition in vertical two-phase flow, Int. J. Multiphase Flow, 18: 847-860. DOI: 10.1016/0301-9322(92)90063-M
- Pushkina, O. L. and Sorokin, Y. L. (1969) Breakdown of liquid film motion in vertical tubes, Heat Transfer Sov. Res., 1, 56-64.
- Wallis, G. B. (1961) Flooding velocities for air and water vertical tubes. UKAA Report, AEEW-R123.

