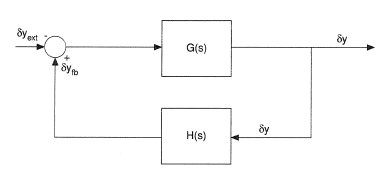
The Nyquist stability criterion has been used extensively in science and engineering to assess the stability of physical systems that can be represented by sets of linear equations. The mathematical foundations of the criterion can be found in many advanced mathematics or linear control theory texts such as Wylie and Barrett (1982), D'Azzo and Houpis (1975) or Willems (1970). The criterion has found popularity partly because of its method of application, which is through a relatively straight-forward geometrical construction. Consider the simple dynamic feedback system represented in the frequency-domain by the following block diagram, Figure 1. This system response dy can be related to the external forcing function δyext by the frequency-domain equation,

The quotient Ф(s) can usually be written so that no singularities appear in the denominator. The system is stable, for a bounded forcing function, if the real parts of the zeros of the denominator have negative real parts. This is because if transformed back into time-domain it is these which form the indices of the exponentials in the solution. The stability of a linear system is thus determined by examining the signs of the real parts of the roots of the characteristic equation. For the simple feedback system described here the characteristic equation is,

The Nyquist criterion considers the variation of the characteristic equation with variation of s over a closed contour C which is formed by a semicircle in the right-hand half of the s-plane and the imaginary axis. Provided that the characteristic equation is analytic everywhere on the closed contour then the net variation of the argument of Ec(s) can be related to the number of poles P and zeros Z of Ec(s) inside C by the following equation,

In geometric terms the number of clockwise encirclements of the origin of the mapping of Ec(s), for a single traverse of s in the s-plane around the contour C, is equal to the difference between the number of zeros and the number of poles of Ec(s) inside C. If the semicircle, or Nyquist "D-contour", is then enlarged to an infinite size, so as to take up the entire right-hand half of the s-plane, the method can be used to check if the characteristic equation has any roots in the right-hand half of the plane. As mentioned earlier it is normally the case that Ф(s) is rearranged so as to remove any poles from Ec(s). It is assumed that this has been done and hence P = 0. If any roots lie in the right-hand half of the plane then they have positive real parts and the system is, therefore, unstable.
For Laplace transforms of most physical systems, the application of the criterion is simplified by the fact that the mapping of s into Ec(s) along the semicircular portion of C collapses onto the origin as the radius of the semicircle tends to an infinite size (see Laplace Transformations.) Furthermore, the mappings along the positive and negative branches of the imaginary axis of s into Ec(s) are symmetric about the real axis. For Laplace transformed systems the application of the Nyquist criterion amounts simply to plotting the locus produced by the mapping of the characteristic equation in its plane (the w-plane), for variation of s along the positive branch of the imaginary axis in the s-plane. In algebraic terms the locus in the w-plane is formed by evaluating,

An example of the application of the criterion is to the stability analysis of boiling channels [Lahey and Podowski (1989)]. A sample Nyquist diagram which shows two loci calculated for a boiling channel is given below. The locus that encircles the origin shows an unstable system and the locus which does not, shows a stable system. (See also Instability, Two-phase.)
To avoid any confusion, it is useful to note that the Nyquist criterion is often applied to the open loop transfer function, G(s)H(s). Stability of the closed loop system is then determined by encirclement of the point (−1,0) in the w-plane.
REFERENCES
D'Azzo, J. J. and Houpis, C. H. (1975) Linear Control System Analysis and Design: Conventional and Modern, McGraw-Hill, USA. DOI: 10.1016/S0016-0032(78)90018-2
Lahey Jr., R. T. & Podowski, M. Z. (1989) On the analysis of various instabilities in two-phase flows, in Multiphase Science and Technology, Eds. G. F. Hewitt, J.-M. Delhaye & N. Zuber, vol. 4, pp 183–370, Hemisphere.
Willems, J. L. (1970) Stability Theory of Dynamical Systems, Nelson, UK. Wylie, C. R. and Barrett, L. C. (1982) Advanced Engineering Mathematics, 5th edn. McGraw-Hill Book Company.
参考文献
- D'Azzo, J. J. and Houpis, C. H. (1975) Linear Control System Analysis and Design: Conventional and Modern, McGraw-Hill, USA. DOI: 10.1016/S0016-0032(78)90018-2
- Lahey Jr., R. T. & Podowski, M. Z. (1989) On the analysis of various instabilities in two-phase flows, in Multiphase Science and Technology, Eds. G. F. Hewitt, J.-M. Delhaye & N. Zuber, vol. 4, pp 183–370, Hemisphere.
- Willems, J. L. (1970) Stability Theory of Dynamical Systems, Nelson, UK. Wylie, C. R. and Barrett, L. C. (1982) Advanced Engineering Mathematics, 5th edn. McGraw-Hill Book Company.