PARALLEL IMPLEMENTATION
Following from: Discrete ordinates and finite volume methods
The computational requirements for the solution of radiative heat transfer problems may be quite large, for example, in the case of 3D, geometrically complex enclosures containing a nongray emitting-absorbing-scattering medium. These requirements become even higher in the case of multimode heat transfer problems and in coupled fluid flow and radiative heat transfer problems. Parallel computing is an effective way to substantially increase the computational speed, since the computational load is distributed among several processors working in parallel on different parts of the problem. Even though the overall required CPU time is not reduced, the wall-clock time can be significantly lower. The use of parallel computing to solve radiative heat transfer problems in participating media is discussed in Gritzo et al. (1995). The present article addresses the parallelization of the discrete ordinates method (DOM) and the finite volume method (FVM).
The radiation intensity depends on the spatial location, direction of propagation, and wavelength. The dependence on time (see article “Transient problems”) is ignored here. In parallel computing, the solution domain is decomposed into subdomains, which are assigned to different processors. Accordingly, there are three ways to parallelize the DOM and the FVM, namely, space, angular, and wavelength domain decomposition. Two or more simultaneous decompositions are possible. The parallelization by wavelength is straightforward, and allows for almost ideal parallel efficiencies if the time required to evaluate the radiative properties is approximately independent on the wavelength. However, it is only applicable to nongray media and is limited by the number of spectral bands in the case of band models, or gray gases, in the case of global models. Angular domain parallelization (ADP) also allows for high parallel efficiencies, being limited by the number of discrete directions (DOM) or solid angles (FVM). Both the wavelength and the angular domain decomposition are limited by the available memory of the processors in distributed memory architectures, since the data for the whole spatial domain must be stored in every processor. Moreover, spatial domain decomposition parallelization (DDP) is usually employed in computational fluid dynamics. Therefore, the DDP is often preferred, even though its parallel efficiency is usually lower than that of the two other options.
Parallelization by wavelength was employed by Benmalek et al. (1996) in a network of seven different workstations. They used the finite element method for spatial discretization and the DOM for angular discretization of the even-parity formulation of the RTE. The parallel code was applied to a nongray, 3D, participating-medium radiative heat transfer problem, and attention was focused on handling failures of workstations and on improving the load balance. An improved version of the spectral model is presented in Tong et al. (1998). Hannebutte and Lewis (1991) used a different approach, suitable to massively parallel architectures. They developed a nonlinear response matrix formalism based on the DOM whose essential feature is that within each computational cell, the temperature is calculated in response to the incoming photons. The method was applied to 2D enclosures with an emitting, absorbing, and isotropically scattering medium.
Most early work on parallelization of the DOM has been carried out in the solution of neutron transport problems, since the Boltzmann transport equation that governs neutron conservation is similar to the RTE. Parallel processing by decomposition into energy groups, which play the same role as the wavelength bands in thermal radiation problems, is presented in Wienke and Hiromoto (1985). Angular decomposition in curvilinear geometries has been addressed in Haghighat (1991) and Mattis and Haghighat (1992), and spatial domain decomposition in Cartesian and curvilinear coordinates has been presented in Yavuz and Larsen (1992) and Mattis and Haghighat (1992), respectively. A DOM matrix method for massively parallel computers is reported in Hannebutte and Lewis (1992). A comprehensive review of this early work on neutron transport problems is presented in Azmy (1997).
Parallel Implementation of the Standard Algorithm
Angular Domain Decomposition
In ADP, the total number of directions along which the RTE is solved is divided into a number of subsets equal to the number of processors. Each processor performs calculations for the whole domain, but treats only a certain subset of directions. Load-balancing problems are avoided if the number of directions is a multiple of the number of processors. The solution algorithm for the DOM is described in Gonçalves and Coelho (1997). The modifications required for the FVM are straightforward (Coelho and Gonçalves, 1999).
The main difference between the solution algorithms for sequential (see article “Solution algorithm”) and parallel processing in ADP is that, in the last case, a processor calculates only a fraction of the incident radiation in every control volume, and incident heat flux on the boundaries, since only the computations for a subset of the total number of directions are carried out in a processor. Following the calculations for its own directions, which are described in step 3 of the algorithm described in the article “Solution algorithm,” every processor broadcasts the contribution of those directions to the incident radiation in every control volume and to the incident heat flux on the walls. Then, the total incident radiation in every control volume and the total incident heat flux on the walls are evaluated in every processor, the boundary conditions are applied, yielding updated radiation intensities leaving the boundaries, and the convergence criteria are checked. If these criteria are not met, a new iteration is performed.
Spatial Domain Decomposition
In the DDP, the computational domain is divided into a number of subdomains equal to the number of processors. In the memory of a processor resides only the geometry and the data of the subdomain allocated to that processor. If the computational domain is mapped using a mesh with Nx × Ny × Nz control volumes, and a 3D array with px × py × pz processors is used, then the number of control volumes assigned to each processor will be (Nx / px) × (Ny / py) × (Nz / pz). Ideal load-balancing is obtained if Nx, Ny, and Nz are integer multiples of px, py, and pz, respectively. Each processor performs calculations for a subdomain, solving the RTE in that subdomain for all the directions. Although the subdomains do not overlap, there is a buffer of halo points added to their boundaries, including the virtual boundaries, i.e., boundaries between neighboring processors, to enable the exchange of data (radiation intensities) at the virtual boundaries between neighboring processors.
The solution algorithm in a processor may be summarized as follows (Gonçalves and Coelho, 1997; Coelho and Gonçalves, 1999):
- Define problem data. Set the incident heat flux on the boundaries and the incident heat radiation in every control volume to 0, and the iteration counter to 1.
- Loop over all the directions (DOM) or solid angles (FVM), and for each one of them loop over the control volumes assigned to the processor; perform the following operations for each control volume:
- Get the incoming radiation intensities at the cell faces from the upstream control volumes or from the boundary conditions, as appropriate according to the subdomain assigned to the processor under consideration. If an upstream control volume lies in a subdomain assigned to a different processor, the required radiation intensities are in the halo region.
- Calculate the grid node radiation intensity.
- Calculate the outgoing radiation intensities at the cell faces.
- Calculate the total incident heat fluxes on the walls.
- Exchange the radiation intensities along the virtual boundaries between neighboring processors.
- Apply the boundary conditions to update the radiation intensities leaving the boundaries.
- Check if the convergence criteria are satisfied. If not, increase the iteration counter by one and return to step 2.
The exchange of data between neighboring processors influences the convergence rate in DDP, i.e., the number of iterations required to achieve convergence, because the radiation intensities available at the halo points of virtual boundaries are those calculated in the previous iteration. In the first iteration, these radiation intensities are guessed, for example, set equal to the radiation intensities at the physical boundaries of the enclosure. The degradation of the convergence rate places an upper limit on the maximum achievable efficiency.
Parallel Performance of ADP and DDP
The parallel performance is usually measured by means of the parallel efficiency Ep and the speedup Sp, which are defined as follows:
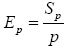
|
(1) |

|
(2) |
where t1 and tp are the wall-clock execution times on one and p processors, respectively. Gonçalves and Coelho (1997) and Coelho and Gonçalves (1999) studied the influence of the number of processors, grid size, order of quadrature, and optical thickness on the parallel performance for both ADP and DDP in emitting-absorbing gray media. The results obtained for the DOM and the FVM are similar. The number of iterations required to achieve convergence is independent of the number of processors for ADP, but increases with the number of processors for DDP, due to the sequential nature of the of the sweeps employed to determine the radiation intensity in every iteration. As a consequence, the parallel efficiency of DDP drops fast with the increase of the number of processors, while the parallel efficiency of ADP also drops, due to the increase of the time required for data exchange among processors (communication time), but more slowly. As an example, parallel efficiencies of 12.5% and 43.2% were found in Gonçalves and Coelho (1997) for DDP and ADP, respectively, for a 3D problem solved using a mesh with 36 × 12 × 12 control volumes, the S8 quadrature, and a distributed memory machine using 80 processors. The parallel efficiency increases with the increase of the grid size and the order of quadrature for ADP, since the ratio of the communication to the execution time decreases in both cases. In the case of DDP, the parallel efficiency also increases with the increase of the grid size, but is independent of the order of quadrature. In a medium with prescribed temperature, the parallel efficiency increases with the increase of the optical thickness of the medium for DDP, but is independent of the optical thickness for ADP.
Burns and Christon (1997) used a similar DDP method to solve a 3D problem in a cube with a nonscattering, absorbing-emitting medium using up to 28 million control volumes and the S10 quadrature. Calculations performed for a fixed number of 393 control volumes per processor yielded parallel efficiencies that range from 45% for eight processors to 9% for 512 processors. Additional calculations carried out for a fixed mesh with 373 control volumes yielded parallel efficiencies that range from 47% for eight processors up to 14% for 216 processors.
Improved Sweeping Strategies for DDP
The parallel efficiency of the DDP method outlined above decreases rapidly as the number of processors increases, due to the sequential nature of the sweeps over the control volume in each subdomain, which is assigned to a different processor. All the processors are working simultaneously on the same discrete direction (in the DOM) or solid angle (in the FVM), and the boundary data they need at the beginning of a sweep is taken from the previous iteration, except for the processors lying on the boundary of the domain for the direction/solid angle under consideration.
It was pointed out in Gonçalves and Coelho (1997) that the convergence rate, and therefore the parallel efficiency, may be improved by alternating the directions along which the RTE is solved for different processors, and exchanging data among processors more frequently. In particular, if only four processors are used in a 2D problem, the number of iterations does not increase compared to the sequential algorithm if the workload is wisely distributed among the processors. To accomplish this goal, every iteration of the solution algorithm is divided into four stages. In the first stage, the directions of every quadrant are treated by a different processor starting from the corners of the domain, sweeping toward the center of the domain, and exchanging data among neighboring processors thereafter. The processors at the bottom-left, bottom-right, top-right, and top-left sides of the domain perform the calculations for all the directions of the first, second, third, and fourth quadrants, respectively. In stages two, three, and four, every processor performs the calculations for a different quadrant in such a way that the radiation intensities at upstream cell faces at the current iteration are available either from the boundary conditions or from control volumes formerly swept (see Gonçalves and Coelho, 1997, for details). This strategy is readily extended to 3D problems and eight processors.
It is not feasible to maintain the convergence rate of a sequential calculation in the case of more than four processors in 2D problems or eight processors in 3D problems, because only the processors on the corners of the domain have access to the boundary values needed to initiate the calculations. However, a few studies have been reported that attempt to distribute more efficiently the workload among the processors in order to increase the speedup of the calculations of the algorithm described above. Yildiz and Bedir (2006) and Chandy et al. (2007) used the same spatial domain decomposition of a rectangular domain, along with a wave front calculation procedure similar to that described above for four or eight processors in 2D or 3D domains, respectively, starting synchronously from every corner of the solution domain. However, the processors are not always busy, as in the above algorithm, but may be idle until the data they need are available. The idea is to always use data (radiation intensities at upstream boundaries) from the current iteration to perform the calculations, at the expense of letting a few processors lay idle until such data are available, in contrast to the algorithm described above where the processors were always busy, but often using data from previous iterations.
Yildiz and Bedir (2006) assign a level number to every control volume of the mesh and for every direction. The level number quantifies how far a control volume is from the upstream boundary of the domain for the direction under consideration. In every iteration of the solution algorithm, the calculations in a processor only start when the radiation intensity at all upstream boundaries of the control volumes of the lower level are available for at least one direction. A processor remains idle while there is no such direction. For a particular direction, the calculations in a processor start from a control volume on the corner of the subdomain assigned to that processor and propagate in a wave front, sweeping control volumes of increasing level. A shifting procedure, analogous to pipelining in vectorial machines, is proposed to maximize the utilization, which is defined as the ratio of the time the processors are busy to the total run time. The shifting procedure consists of an idle stage before the wave fronts are initiated to improve load balancing and maximize utilization. The calculation of the level number of the control volumes and utilization of the processors may be determined a priori for different subdomain partitions and angular quadratures of the DOM. In this way, the order of calculation of the directions is determined for every processor.
Chandy et al. (2007) developed a marching method referred to as the staged technique, which relies on a priority queuing system in which the calculations are organized and prioritized dynamically based on data availability. Their study is developed for nonscattering media and upwind finite-differencing schemes. The method is very similar to that used by Yildiz and Bedir (2006), but it is unclear whether the sweeping order is identical in both cases or not. Calculations performed for a 3D problem with black boundaries using a mesh with 128 × 128 × 128 control volumes, the S6 quadrature, and 32 processors reveal that the iterative technique of Gonçalves and Coelho (1997) and Burns and Christon (1997) yields a speedup of about 2, while this staged technique achieves a speedup of about 10. An increase of the parallel efficiency with the problem size was found.
Plimpton et al. (2005) presented algorithms to improve the parallel efficiency in unstructured grids for the solution of the Boltzmann transport equation using the DOM. The algorithms are also applicable to structured grids and to the solution of the RTE. A basic parallel sweeping algorithm is described that allows different processors to perform simultaneous sweeps for different directions and energy groups (spectral bands, in the case of the RTE). Two improvements of this basic algorithm are reported, namely, a simple geometric heuristic for prioritizing the control volume/direction tasks each processor works on, and a partitioning algorithm that can reduce the time processors are idle waiting for other processors’ computations. Parallel efficiencies of over 50% for the basic parallel sweeping algorithm and up to 80% with the two improvements were obtained for a mesh with about 3 million control volumes using 2048 processors. A similar parallel sweeping algorithm for unstructured grids is presented in Pautz (2002). However, the ordering of the control volumes in Plimpton et al. (2005) is based on geometrical considerations, while in Pautz (2002) is based on graph theory.
In the works described above, the computational domain is divided into a number of rectangular continuous subdomains equal to the number of processors, and each subdomain is assigned to a different processor. Bailey and Falgout (2009) compare a few algorithms in which the computational domain is divided into a number of rectangular continuous subdomains that may exceed the number of processors, and several discontinuous subdomains may be assigned to the same processor, with the same number of subdomains per processor. The sweeping algorithms compared in Bailey and Falgout (2009) are the Koch-Baker-Alcouffe algorithm (Koch et al., 1992), a data-driven algorithm (Dorr and Still, 1996), and the Compton and Clouse (2005) algorithm. The domain decomposition in these algorithms is illustrated in Fig. 1. Although the parallel efficiency of these sweeping algorithms may be higher than that of those with one subdomain per processor, they are not suitable for coupled fluid flow radiative transfer problems.
 |
 |
| (a) | (b) |
Figure 1. Domain decomposition for several sweeping algorithms, where the thin lines identify the control volumes, the thick lines identify the boundaries of the subdomains, and the numbers indicate the processor number assigned to a subdomain: (a) data-driven algorithm (Dorr and Still, 1996); (b) Koch-Baker-Alcouffe algorithm (Koch et al., 1992); (c) Compton-Clouse algorithm (Compton and Clouse, 2005)
A theoretical analysis of the scaling of sweep algorithms is reported in Bailey and Falgout (2009) for the solution of the Boltzmann equation in the framework of neutron transport problems. This analysis is readily applicable to the RTE and the DOM and FVM. In all algorithms, each processor runs iteratively a do-while loop over all directions constituted by three steps, namely, (i) choice of direction and subdomain that are ready to sweep, (ii) calculation of the radiation intensity (in the case of the RTE) in the control volumes of the selected subdomain, and (iii) communication of the boundary data with neighboring processors. Each step of this loop is synchronized to begin at the same time on all processors. A processor may be idle in steps (i) and (ii) of the algorithm if there is not enough boundary data to perform the calculations of the radiation intensity in its subdomain. The sweeping algorithms differ in the domain decomposition, processor grid layout, and selection of direction in step (i) of the loop mentioned above. Bailey and Falgout (2009) showed that sweeping a small number of directions during each stage (execution of steps i, ii, and iii of the loop) enhances the scalability of the algorithm. Scalability is also improved by increasing the ratio of subdomains to processors.
Parallel Implementation of other Solution Algorithms
Other solution algorithms of the DOM and FVM were described in the article “Solution algorithm.” Among them, the parallelization of Krylov subspace iterative methods for the solution of the system of discrete algebraic equations is addressed in Liu et al. (1999), Krishnamoorthy et al. (2005a,b), and Godoy and DesJardin (2010).
Liu et al. (1999) applied the DDP to unstructured meshes for 2D and 3D problems, which were solved using the FVM. The DDP strategy was used by equally partitioning the spatial domain along the longer geometric dimension. The solver is a preconditioned conjugate gradient method. The parallel efficiency decreased significantly with the increase of the number of processors. In the case of a 3D problem solved in a computer with 18 processors, using a mesh with about 28 × 103 control volumes and the S4 quadrature, the parallel efficiency ranged from about 40% to less than 20%, depending on the radiative properties of the medium. The parallel performance decreases with the increase of the absorption coefficient if the temperature of the medium is fixed, but increases if a heat source is prescribed. The former conclusion is opposite to that drawn in Gonçalves and Coelho (1997), the difference being probably due to the different algorithms employed.
Krishnamoorthy et al. (2005a) solved the same problem as Burns and Christon (1997) using the DOM. They employed two different solvers, namely, GMRES (Saad and Schultz, 1986) and BiCGSTAB (Van der Vorst, 1992), with point Jacobi or block Jacobi preconditioning. The block Jacobi was found to be more efficient than the point Jacobi preconditioning. The parallel performance of BiCGSTAB was slightly better than that of GMRES for a small number of processors, but little differences between the two solvers were found for a large number of processors. Calculations performed for a fixed number of 373 control volumes per processor and a quadrature with 80 directions yielded parallel efficiencies that ranged from 71% for eight processors to 4% for 125 processors, taking as a reference (efficiency of 100%) calculations performed using two processors. In the case of a fixed number of 1213 control volumes per processor, the parallel efficiencies increased to 91% for eight processors and 67% for 125 processors, taking again the solution for two processors as a reference. Additional calculations carried out for a fixed mesh with 253 control volumes yielded parallel efficiencies that ranged from 31% for eight processors to 12% for 64 processors. The parallel efficiency of a 1D problem solved using a 3D mesh did not depend strongly on the optical thickness of the medium, in contrast to previous works. Nongray media were considered in Krishnamoorthy et al. (2005b), but the parallelization was still implemented using DDP.
Godoy and DesJardin (2010) also applied DDP to the DOM. The solution of the system of discrete algebraic equations was carried out using the GMRES method. No details about the parallel efficiency of the implementation were given.
Parallel Implementation of Alternative Formulations
Alternative formulations of the DOM and FVM were described in the article “Alternative formulations.” Among them is the finite element method for spatial discretization along with the DOM for angular discretization, and the discrete ordinates with time stepping (DOTS) (Fiterman et al., 1999). The latter method transforms the RTE to an initial-value problem by adding a time derivative term, and uses an explicit pseudo–time-stepping iterative procedure.
Burns (1997) used a finite element spatial discretization while retaining the DOM for angular discretization. Even though the formulation is applicable to unstructured meshes, only results for a uniform, structured, rectangular mesh were presented. Three different solvers were compared, namely, the Gauss-Seidel (GS) method with no preconditioning and an underrelaxation factor of 0.4, the conjugate gradient squared (CGS) method with diagonal (Jacobi) preconditioning, and the stabilized biconjugate gradient (Bi-CGSTAB) method with diagonal preconditioning (see article “Solution algorithms”). The problem formerly solved by Burns and Christon (1997) was addressed again. The parallel performance was significantly better than that reported in Burns and Christon (1997), which is attributed to improvements in the sparse matrix iterative solution algorithm. In the case of a fixed mesh with 313 control volumes and the S10 quadrature, the parallel efficiency of the DDP was about 90% for eight processors using the Bi-CGSTAB and GS, and exceeded 100% using the CGS, due to a decrease of the number of iterations required over the single-processor case. In the case of 27 processors, the parallel efficiencies were 62% for the Bi-CGSTAB, 67% for the GS, and 80% for the CGS. The parallel efficiency is reduced in the case of a coarser mesh. Results for ADP have also been presented.
A parallel implementation of the DOTS formulation (see article “Alternative formulations”) is reported in Tal et al. (2003). The spatial and the angular discretization were carried out using the finite volume method, and the pseudo time discretization was performed using the explicit Euler method. A shared-memory vector machine with 16 processors was used. Parallel efficiencies of DDP up to 95% for 16 processors were obtained, which largely exceeds the results obtained using the standard formulation. This is attributed to two reasons. One is the explicit nature of the algorithm. The calculation of the radiation intensity at a control volume in a time step only requires data from the previous time step, which are fully available. This means that the convergence rate, i.e., the number of iterations required to achieve a converged solution, is the same regardless of the number of processors. The other reason is the use of a shared-memory machine that almost eliminates the need for additional storage and communications overhead. The authors speculate that it is possible to implement the same method in a distributed-memory machine and still achieve high parallel efficiencies. While this is likely to be true, it remains an open issue. It was further found that the parallel efficiency is independent of the optical thickness of the medium, and decreases marginally with the increase of the number of ordinates.
REFERENCES
Azmy, Y. Y., Multiprocessing for Neutron Diffusion and Deterministic, Transport Prog. Nucl. Energy, vol. 31, no. 3, pp. 317−368, 1997.
Bailey, T. S. and Falgout, R. D., Analysis of Massively Parallel Discrete-Ordinates Transport Sweep Algorithms with Collisions, Int. Conf. on Mathematics, Computational Methods and Reactor Physics, Saratoga Springs, New York, May 3−7, 2009.
Benmalek, A., Tong, T. W., and Li, W., Distributed-Memory Parallel Algorithm for the Solution of the Spectral Radiative Transfer Equation, AIAA Paper No. 96−0606, 1996.
Burns, S. P., Application of Spatial and Angular Domain Based Parallelism to a Discrete Ordinates Formulation with Unstructured Spatial Discretization, 2nd Int. Symp. on Radiative Heat Transfer, M. P. Mengüç, Ed., New York and Redding, CT: Begell House, pp. 173−193, 1997.
Burns, S. P. and Christon, M. A., Spatial Domain-Based Parallelism in Large Scale, Participating-Media, Radiative Transport Applications, Numer. Heat Transfer, Part B, vol. 31, no. 4, pp. 401−422, 1997.
Chandy, A. J., Glaze, D. J., and Frankel, S. H., Parallelizing the Discrete Ordinates Method (DOM) for Three-Dimensional Radiative Heat Transfer Calculations Using a Priority Queuing Technique, Numer. Heat Transfer, Part B, vol. 52, pp. 33−49, 2007.
Coelho, P. J. and Gonçalves, J., Parallelization of the Finite Volume Method for Radiation Heat Transfer, Int. J. Numer. Methods Heat Fluid Flow, vol. 9, no. 4, pp. 388−404, 1999.
Compton, J. C. and Clouse, J. C., Tiling Models for Spatial Decomposition in AMTRAN, Proc. of Joint Russian-American Five-Laboratory Conference on Computational Mathematics/Physics, Vienna, June 19−23, 2005.
Dorr, M. R. and Still, C. H., Concurrent Source Iteration in the Solution of Three-Dimensional, Multigroup, Discrete Ordinates Neutron Transport, Nucl. Sci. Eng., vol. 122, no. 3, pp. 287−308, 1996.
Fiterman, A., Ben-Zvi, R., and Kribus, A., DOTS: Pseudo-Time-Stepping Solution of the Discrete Ordinate Equations, Numer. Heat Transfer, Part B, vol. 35, pp. 163−183, 1999.
Godoy, W. F. and Desjardin, P. E., On the Use of Flux Limiters in the Discrete Ordinates Method for 3D Radiation Calculations in Absorbing and Scattering Media, J. Comput. Phys., vol. 229, pp. 3189−3213, 2010.
Gonçalves, J. and Coelho, P. J., Parallelization of the Discrete Ordinates Method, Numer. Heat Transfer, Part B, vol. 32, no. 2, pp. 151−173, 1997.
Gritzo, L. A., Skocypec, R. D., and Tong, T. W., The Use of High-Performance Computing to Solve Participating Media Radiative Heat Transfer Problems-Results of an NSF Workshop, Sandia Report No. SAND95−0225, 1995.
Haghighat, A., Angular Parallelization of a Curvilinear Sn Transport Theory Method, Nucl. Sci. Eng., vol. 108, pp. 267−277, 1991.
Hannebutte, U. R. and Lewis, E. E., A Massively Parallel Algorithm for Radiative Transfer Calculations, ASME Paper No. 91−WA−HT−10, 1991.
Hannebutte, U. R. and Lewis, E. E., A Massively Parallel Discrete Ordinates Response Matrix Method for Neutron Transport, Nucl. Sci. Eng., vol. 111, pp. 46−56, 1992.
Koch, K. R., Baker, R. S., and Alcouffe, R. E., Solution of First-Order Form of Three-Dimensional Discrete Ordinates Equations on a Massively Parallel Machine, Trans. Am. Nucl. Soc., vol. 65, pp. 198−199, 1992.
Krishnamoorthy, G., Rawat, R., and Smith, P. J., Parallel Computations of Radiative Heat Transfer Using the Discrete Ordinates Method, Numer. Heat Transfer, Part B, vol. 46, pp. 19−38, 2005a.
Krishnamoorthy, G., Rawat, R., and Smith, P. J., Parallel Computations of Nongray Radiative Heat Transfer, Numer. Heat Transfer, Part B, vol. 48, pp. 191−211, 2005b.
Liu, J., Shang, H. M., and Chen, Y. S., Parallel Simulation of Radiative Heat Transfer Using an Unstructured Finite-Volume Method, Numer. Heat Transfer, Part B, vol. 36, pp. 115−137, 1999.
Mattis, R. and A. Haghighat, A., Domain Decomposition of a Two-Dimensional Sn Method, Nucl. Sci. Eng., vol. 111, pp. 180−196, 1992.
Pautz, S. D., An Algorithm for Parallel Sn Sweeps on Unstructured Meshes, Nucl. Sci. Eng., vol. 140, pp. 111−136, 2002.
Plimpton, S. J., Hendrickson, B., Burns, S. P., McLendon III, W., and Rauchwerger, L., Parallel Sn Sweeps on Unstructured Grids: Algorithms for Prioritization, Grid Partitioning, and Cycle-Detection, Nucl. Sci. Eng., vol. 150, pp. 267−283, 2005.
Saad, S. and Schultz, M. H., GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems, SIAM J. Scientific Stat. Comput., vol. 7, no. 3, pp. 856−869, 1986.
Tal, J., Ben-Zvi, R., and Kribus, A., A High-Efficiency Parallel Solution of the Radiative Transfer Equation, Numer. Heat Transfer, Part B, vol. 44, pp. 295−308, 2003.
Tong, T. W., Hoover, R. L., and Li, W., Parallel Computing of Participating-Media Radiative Heat Transfer, Proc. of 11th Int. Heat Transfer Conference, vol. 7, pp. 481−486, 1998.
Van der Vorst, H. A., Bi-CGSTAB: A Fast and Smoothly Converging Variant of Bi-CG for the Solution of Nonsymmetric Linear Systems, SIAM J. Sci. Stat. Comput., vol. 13, pp. 631−644, 1992.
Wienke, B. R. and Hiromoto, R. E., Parallel Sn Iteration Schemes, Nucl. Sci. Eng., vol. 90, pp. 116−123, 1985.
Yavuz, V and Larsen, E. W., Iterative Methods for Solving x-y Geometry Sn Problems on Parallel Architecture Computers, Nucl. Sci. Eng., vol. 112, pp. 32−42, 1992.
Yildiz, Ö and Bedir, H., A Parallel Solution to the Radiative Transport in Three-Dimensional Participating Media, Numer. Heat Transfer, Part B, vol. 50, pp. 79−95, 2006.
Les références
- Azmy, Y. Y., Multiprocessing for Neutron Diffusion and Deterministic, Transport Prog. Nucl. Energy, vol. 31, no. 3, pp. 317−368, 1997.
- Bailey, T. S. and Falgout, R. D., Analysis of Massively Parallel Discrete-Ordinates Transport Sweep Algorithms with Collisions, Int. Conf. on Mathematics, Computational Methods and Reactor Physics, Saratoga Springs, New York, May 3−7, 2009.
- Benmalek, A., Tong, T. W., and Li, W., Distributed-Memory Parallel Algorithm for the Solution of the Spectral Radiative Transfer Equation, AIAA Paper No. 96−0606, 1996.
- Burns, S. P., Application of Spatial and Angular Domain Based Parallelism to a Discrete Ordinates Formulation with Unstructured Spatial Discretization, 2nd Int. Symp. on Radiative Heat Transfer, M. P. Mengüç, Ed., New York and Redding, CT: Begell House, pp. 173−193, 1997.
- Burns, S. P. and Christon, M. A., Spatial Domain-Based Parallelism in Large Scale, Participating-Media, Radiative Transport Applications, Numer. Heat Transfer, Part B, vol. 31, no. 4, pp. 401−422, 1997.
- Chandy, A. J., Glaze, D. J., and Frankel, S. H., Parallelizing the Discrete Ordinates Method (DOM) for Three-Dimensional Radiative Heat Transfer Calculations Using a Priority Queuing Technique, Numer. Heat Transfer, Part B, vol. 52, pp. 33−49, 2007.
- Coelho, P. J. and Gonçalves, J., Parallelization of the Finite Volume Method for Radiation Heat Transfer, Int. J. Numer. Methods Heat Fluid Flow, vol. 9, no. 4, pp. 388−404, 1999.
- Compton, J. C. and Clouse, J. C., Tiling Models for Spatial Decomposition in AMTRAN, Proc. of Joint Russian-American Five-Laboratory Conference on Computational Mathematics/Physics, Vienna, June 19−23, 2005.
- Dorr, M. R. and Still, C. H., Concurrent Source Iteration in the Solution of Three-Dimensional, Multigroup, Discrete Ordinates Neutron Transport, Nucl. Sci. Eng., vol. 122, no. 3, pp. 287−308, 1996.
- Fiterman, A., Ben-Zvi, R., and Kribus, A., DOTS: Pseudo-Time-Stepping Solution of the Discrete Ordinate Equations, Numer. Heat Transfer, Part B, vol. 35, pp. 163−183, 1999.
- Godoy, W. F. and Desjardin, P. E., On the Use of Flux Limiters in the Discrete Ordinates Method for 3D Radiation Calculations in Absorbing and Scattering Media, J. Comput. Phys., vol. 229, pp. 3189−3213, 2010.
- Gonçalves, J. and Coelho, P. J., Parallelization of the Discrete Ordinates Method, Numer. Heat Transfer, Part B, vol. 32, no. 2, pp. 151−173, 1997.
- Gritzo, L. A., Skocypec, R. D., and Tong, T. W., The Use of High-Performance Computing to Solve Participating Media Radiative Heat Transfer Problems-Results of an NSF Workshop, Sandia Report No. SAND95−0225, 1995.
- Haghighat, A., Angular Parallelization of a Curvilinear Sn Transport Theory Method, Nucl. Sci. Eng., vol. 108, pp. 267−277, 1991.
- Hannebutte, U. R. and Lewis, E. E., A Massively Parallel Algorithm for Radiative Transfer Calculations, ASME Paper No. 91−WA−HT−10, 1991.
- Hannebutte, U. R. and Lewis, E. E., A Massively Parallel Discrete Ordinates Response Matrix Method for Neutron Transport, Nucl. Sci. Eng., vol. 111, pp. 46−56, 1992.
- Koch, K. R., Baker, R. S., and Alcouffe, R. E., Solution of First-Order Form of Three-Dimensional Discrete Ordinates Equations on a Massively Parallel Machine, Trans. Am. Nucl. Soc., vol. 65, pp. 198−199, 1992.
- Krishnamoorthy, G., Rawat, R., and Smith, P. J., Parallel Computations of Radiative Heat Transfer Using the Discrete Ordinates Method, Numer. Heat Transfer, Part B, vol. 46, pp. 19−38, 2005a.
- Krishnamoorthy, G., Rawat, R., and Smith, P. J., Parallel Computations of Nongray Radiative Heat Transfer, Numer. Heat Transfer, Part B, vol. 48, pp. 191−211, 2005b.
- Liu, J., Shang, H. M., and Chen, Y. S., Parallel Simulation of Radiative Heat Transfer Using an Unstructured Finite-Volume Method, Numer. Heat Transfer, Part B, vol. 36, pp. 115−137, 1999.
- Mattis, R. and A. Haghighat, A., Domain Decomposition of a Two-Dimensional Sn Method, Nucl. Sci. Eng., vol. 111, pp. 180−196, 1992.
- Pautz, S. D., An Algorithm for Parallel Sn Sweeps on Unstructured Meshes, Nucl. Sci. Eng., vol. 140, pp. 111−136, 2002.
- Plimpton, S. J., Hendrickson, B., Burns, S. P., McLendon III, W., and Rauchwerger, L., Parallel Sn Sweeps on Unstructured Grids: Algorithms for Prioritization, Grid Partitioning, and Cycle-Detection, Nucl. Sci. Eng., vol. 150, pp. 267−283, 2005.
- Saad, S. and Schultz, M. H., GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems, SIAM J. Scientific Stat. Comput., vol. 7, no. 3, pp. 856−869, 1986.
- Tal, J., Ben-Zvi, R., and Kribus, A., A High-Efficiency Parallel Solution of the Radiative Transfer Equation, Numer. Heat Transfer, Part B, vol. 44, pp. 295−308, 2003.
- Tong, T. W., Hoover, R. L., and Li, W., Parallel Computing of Participating-Media Radiative Heat Transfer, Proc. of 11th Int. Heat Transfer Conference, vol. 7, pp. 481−486, 1998.
- Van der Vorst, H. A., Bi-CGSTAB: A Fast and Smoothly Converging Variant of Bi-CG for the Solution of Nonsymmetric Linear Systems, SIAM J. Sci. Stat. Comput., vol. 13, pp. 631−644, 1992.
- Wienke, B. R. and Hiromoto, R. E., Parallel Sn Iteration Schemes, Nucl. Sci. Eng., vol. 90, pp. 116−123, 1985.
- Yavuz, V and Larsen, E. W., Iterative Methods for Solving x-y Geometry Sn Problems on Parallel Architecture Computers, Nucl. Sci. Eng., vol. 112, pp. 32−42, 1992.
- Yildiz, Ö and Bedir, H., A Parallel Solution to the Radiative Transport in Three-Dimensional Participating Media, Numer. Heat Transfer, Part B, vol. 50, pp. 79−95, 2006.
