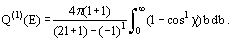The kinetic theory of gases is concerned with molecules in motion and with the microscopic and macroscopic consequences of such motion in a gas. Kinetic theory can be used to deduce some of the equilibrium properties of gases, but the methods of statistical thermodynamics are more powerful in that respect. The importance of kinetic theory lies in its ability to describe nonequilibrium phenomena such as the transport of heat or of momentum in a slightly nonuniform gas or the scattering of molecules by other molecules. Much of modern kinetic theory is due to the efforts of Maxwell, Boltzmann, Enskog and Chapman in the late 19th century and the early 20th century. In this article, emphasis will be placed on the results of these efforts; little attention will be given to the mathematical details involved [Chapman and Cowling (1970)].
The results of kinetic theory may be built up from the kinematics of binary molecular encounters to yield a description of the transport properties of gases at such densities that binary but not ternary collisions are important. For monatomic gases, this theory is both complete and easily applicable [Maitland et al. (1981)]; the microscopic and macroscopic results are presented below. There is no entirely satisfactory kinetic theory for gases at high densities or for liquids although the theory due to Enskog, which will be described briefly, is of some use. For polyatomic gases, the theory is made vastly more complicated by two facts. First, the forces between molecules depend not only upon intermolecular separation but also on the mutual orientation of the molecules. Second, polyatomic molecules have rotational and vibrational degrees of freedom which play an important role in determining the outcome of a collision between molecules. Although much of the relevant theory has been derived in a formal sense, it is, at present, extremely difficult to apply [Maitland et al. (1981)]. Consequently, simplified results will be discussed, from which the transport properties of polyatomic gases may be determined approximately [Reid et al. (1977)].
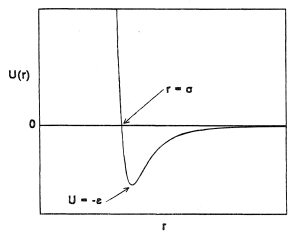
The kinematics of a binary collision between two spherically-symmetric molecules are easily derived. The forces between two such molecules act along the intermolecular axis and are a function of the separation r only. The potential energy U(r) stored in the intermolecular forces therefore also a function only of the separation. The general form of this function is illustrated in Figure 1.
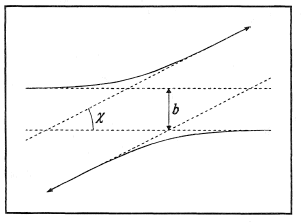
The kinetic energy of a pair of molecules can be separated into the sum of two independent terms; one relating to the motion of the center of mass and the other, to the relative motion of the two molecules. Thus, in studying an encounter or collision between two molecules, it will be sufficient to consider only the relative motion in a body-fixed coordinate system with axes parallel to the space-fixed frame of reference and origin located at the center of mass of the two molecules. In this frame, the relative trajectories of two molecules are always parallel. A typical case is illustrated in Figure 2. The initial and final trajectories are specified by the initial relative kinetic energy E, the impact parameter b, and the angle of deflection χ.
Both energy and angular momentum are conserved in the encounter and the angle of deflection [Guggenheim (I960)] is
where r0 is the distance of closest approach during the encounter:

Although individual collisions cannot be studied experimentally, the scattering of molecular beams may be observed and is quantified in terms of scattering cross sections. In a typical experimental apparatus, two beams of particles with selected narrow velocity ranges are crossed and the scattered flux is measured as a function of the scattering angle χ. The differential scattering cross-section σ(χ,E) is defined as the ratio of the number of scattered particles per unit time per unit solid angle to the number of incident particles per unit time per unit area. This is a function of relative initial kinetic energy and the angle of scattering. The differential cross-section is given by:

or, when more than one impact parameter leads to the same scattering angle, by a sum of such terms. Sometimes, only the integral cross-section Q(E) is measured:

These quantities may be used to infer information about the intermolecular potential U(r) [Maitland et al. (1981)].
For polyatomic molecules, the description is much more complicated and inelastic scattering is possible in which there is a change in the internal state of one or both molecules such that the initial and final relative kinetic energies differ. These complications will not be considered further here.
The kinetic theory of gases in bulk is described in detail by the famous Boltzmann equation This is an integro-differential equation for the distribution function f(r,u,t), where f dxdydzdudvdw is the probable number of molecules whose centers have, at time t, positions in the ranges x to x + dx, y to y + dy, z to z + dz, and velocity components in the ranges u to u + du, v to v + dv, w to w + dw. For a gas in a state of thermodynamic equilibrium, this reduces to the Maxwell-Boltzmann Velocity Distribution Function, from which quantities such as mean speed, mean collision rate and mean free path may be determined. However, the Boltzmann equation may also be solved for cases in which small macroscopic gradients exist in either (bulk) velocity, temperature or composition. The solutions give the relation between the gradient and the corresponding flux in each case in terms of collision cross-sections. The coefficients of Viscosity, Thermal Conductivity and Diffusion are thereby related to intermolecular potential.
The Chapman-Enskog solution of the Boltzmann equation is mathematically complicated but it leads to comparatively simple results [Chapman and Cowling (1970)]. The transport coefficients are given in terms of a set of temperature-dependent collision integrals  which are themselves given in terms of a set of energy-dependent transport cross-sections Q(l)(E). Finally these, transport cross-sections are related to the angle of deflection χ(b,E). Specifically, the results are [Maitland et al. (1981)]:
which are themselves given in terms of a set of energy-dependent transport cross-sections Q(l)(E). Finally these, transport cross-sections are related to the angle of deflection χ(b,E). Specifically, the results are [Maitland et al. (1981)]:
and
where m is the mass of one molecule, k is Boltzmann's constant, and cv is the specific heat capacity at constant volume,
and
Equations (5) and (6) are in fact only first-order approximations of the transport coefficients, but the necessary corrections to these formulas are usually less than 1%. It is worth noting that in this approximation, both η and λ depend upon the same collision integral and that the ratio λ/η in a monatomic gas is simply 5cv/2 (for monatomic gases, cv = 3k/2m).
For rigid spherical molecules of diameter d, the integrals (Equations (1), (7) and (8)) may be evaluated analytically with the results that cos(χ/2) = (b/d) for all E, Q(l)(E) = πd2 for all E and  = πd2 for all T. The coefficients of viscosity and thermal conductivity for this model are therefore
= πd2 for all T. The coefficients of viscosity and thermal conductivity for this model are therefore

and

For other intermolecular potentials, the integrals may be evaluated by quadrature [Maitland et al. (1981)]. Equation (9) is often applied to obtain from viscosity data a rough estimate of the size of a molecule and hence, its mean free path.
The kinetic theory may be applied also to the transport coefficients of monatomic gas mixtures. The diffusion coefficient D12 in a binary mixture is:

where  is the number density of molecules, μ12 is the reduced mass m1m2/(m1 + m2), and
is the number density of molecules, μ12 is the reduced mass m1m2/(m1 + m2), and  is the collision integral evaluated through Equations (1), (7) and (8) with U equal to the unlike intermolecular potential U12 between molecules of types 1 and 2. The exact results for ηmix and λmix are quite complicated but differ little from the following simple approximations:
is the collision integral evaluated through Equations (1), (7) and (8) with U equal to the unlike intermolecular potential U12 between molecules of types 1 and 2. The exact results for ηmix and λmix are quite complicated but differ little from the following simple approximations:

and
with

An important feature of the results is that the transport coefficients obey a principle of corresponding states amongst any set of substances whose intermolecular potentials may be written in the form:
Here, ε and σ are scaling parameters for length and energy (defined in Figure 1) appropriate to a particular substance and F is a universal function. When Equation (15) holds, the collision integrals are given by

where  is a reduced collision integral determined by the form of the function F and T* = kT/ε is the reduced temperature. For nonattracting rigid spherical molecules of diameter d = σ, all of the reduced collision integrals are unity, whereas for real molecules, these integrals vary slowly with temperature as illustrated in Figure 3. Tables of reduced collision integrals are available for a number of model intermolecular potential functions which conform to Equation (15) and scaling parameters are available for many substances [Reid et al. (1977)]. Universal correlations of the collision integrals
is a reduced collision integral determined by the form of the function F and T* = kT/ε is the reduced temperature. For nonattracting rigid spherical molecules of diameter d = σ, all of the reduced collision integrals are unity, whereas for real molecules, these integrals vary slowly with temperature as illustrated in Figure 3. Tables of reduced collision integrals are available for a number of model intermolecular potential functions which conform to Equation (15) and scaling parameters are available for many substances [Reid et al. (1977)]. Universal correlations of the collision integrals  and
and  based on experimental data are also available, together with scaling parameters for a number of simple molecules [Maitland et al. (1981)]. Alternative correlations of transport coefficients in terms of the critical constants are available for cases in which suitable scaling parameters based on Equation (15) are unavailable [Reid et al. (1977)].
based on experimental data are also available, together with scaling parameters for a number of simple molecules [Maitland et al. (1981)]. Alternative correlations of transport coefficients in terms of the critical constants are available for cases in which suitable scaling parameters based on Equation (15) are unavailable [Reid et al. (1977)].
As indicated above, the formal theory is much more complicated for polyatomic gases because of the possibility of inelastic collisions, and is very difficult to apply. Fortunately, it appears that the effects of inelastic collisions on the coefficients of viscosity and diffusion are not usually more than a few percent. Furthermore, it is an empirical fact that scaling parameters ε and σ can be found such that the viscosity and diffusion coefficients of polyatomic gases follow the same principle of corresponding states as do monatomic gases. Thus η and D12 may be predicted for pure polyatomic gases and for mixtures containing polyatomic components, provided that some data is available from which to determine the required values of ε and σ.
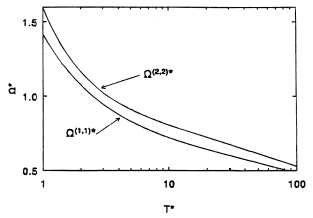
Figure 3. Reduced collision integrals determined from the principle of corresponding states. Source: Maitland et al. (1981).
The thermal conductivity of polyatomic gases is influenced considerably by inelastic collisions and cannot therefore be obtained with any accuracy from the monatomic theory or from the principle of corresponding states. A number of approximate treatments are available by which λ is represented as the sum of two terms: one (λtrans) relating to the transport of translational energy and the other (λint), to the transport of internal molecular energy. In the simplest treatment, the ratio λtrans/η is set equal to its value in a monatomic gas, (15R/4M) and the internal energy of the molecules is assumed to be transported at the same rate as the molecules themselves by the process of diffusion. The result of this treatment is the formula
in which Δ = 3k/2mcv and D is the coefficient of self diffusion. The ratio (ρD/π) is given by

and it turns out that this has an almost constant value of 4/3. Equation (17) is based on the assumption that inelastic collisions are rare. If the opposite assumption is made, namely that translational and internal energy are exchanged easily in collisions, then the Eucken expression is obtained:
Usually, the ratio λ/ηcv lies somewhere in between the values given by Equations (17) and (19). A more accurate treatment requires information on the frequency of inelastic collisions, but this is available from experiment in only a few cases. Thus, an approximation such as Equation (19) is often the best that can be done. Application of this formula requires η, which may be estimated using the monatomic theory or the principle of corresponding states, and cv Once pure component thermal conductivities have been estimated in this crude way, one might as well estimate λmix from Equation (13).
All of the kinetic theory discussed above applies only to gases at densities which are large enough that the mean free path is small compared with the dimensions of the container and, at the same time, small enough that only binary collisions are important. At very low densities, thermal conductivity and viscosity are smaller than those of the dilute-gas theory (Equations (5) and (6)) and, ultimately, they can be reduced in proportion to the density. Otherwise, the transport coefficients are slowly varying function of ρ which, ignoring the very low density regime, extrapolate to the dilute-gas values as ρ → 0. For gases at atmospheric pressure, the transport coefficients differ little from these ‘zero-density’ values but at higher pressures, significant variation is found. Unfortunately, there is no satisfactory theory to account for density dependence of the transport coefficients. The theory of Enskog [Hirschfelder et al. (1964)] is based on a model in which the molecules are treated as rigid elastic spheres and, although it gives results that agree with computer simulations of hard-sphere transport properties, the results as applied to real gases are disappointing. Various modifications have been proposed that go some way to alleviating this situation.
REFERENCES
Chapman, S. and Cowling, T. G. (1970) The Mathematical Theory of Non-Uniform Gases (3rd edn). Cambridge University Press. London.
Guggenheim, E. A. (1960) Elements of the Kinetic Theory of Gases. Pergamon Press. Oxford. DOI: 10.1016/0017-9310(61)90081-3
Hirschfelder, J. O., Curtiss, C. R, and Bird, R. B. (1964) Molecular Theory of Gases and Liquids (Corrected Edition). Wiley. New York.
Maitland, G. C., Rigby, M., Smith, E. B., and Wakeham, W. A. (1981) Intermolecular Forces, Their Origin and Determination. Clarendon Press. Oxford.
Reid, R. C., Prausnitz, J. M., and Sherwood, T. K. (1977) The Properties of Gases and Liquids (3rd edn). McGraw-Hill. New York.
Les références
- Chapman, S. and Cowling, T. G. (1970) The Mathematical Theory of Non-Uniform Gases (3rd edn). Cambridge University Press. London. DOI: 10.1002/zamm.19920721124
- Guggenheim, E. A. (1960) Elements of the Kinetic Theory of Gases. Pergamon Press. Oxford. DOI: 10.1016/0017-9310(61)90081-3
- Hirschfelder, J. O., Curtiss, C. R, and Bird, R. B. (1964) Molecular Theory of Gases and Liquids (Corrected Edition). Wiley. New York.
- Maitland, G. C., Rigby, M., Smith, E. B., and Wakeham, W. A. (1981) Intermolecular Forces, Their Origin and Determination. Clarendon Press. Oxford.
- Reid, R. C., Prausnitz, J. M., and Sherwood, T. K. (1977) The Properties of Gases and Liquids (3rd edn). McGraw-Hill. New York.