The Laplace transform is the basis of operational methods for solving linear problems described by differential or integro-differential equations. The Laplace transform involves the transformation of a complex function f(t) of the real argument t, which satisfies Gelder's condition, |f(t + h)f(t)| ≤ A|h|α, α ≤ 1, |h| < h0, the bounded growth condition, |f(t)| < M  (S0 is the index of growth); and the condition f(t) = 0 for t < 0. The Laplace transform has the form
(S0 is the index of growth); and the condition f(t) = 0 for t < 0. The Laplace transform has the form

Here f(t) is the function-original, F(p) is the Laplace transform of function f(t); and p = s + iσ, the complex variable.
For any original function f(t), the transform of F(p) can be defined in a half-plane Re p < s0, where s0 is the growth index of f(t). If the function f(t) is bounded, |f(t)| < M for all t, then s0 = 0.
To reconstruct the original of f(t) from the transform F(p), the inverse Laplace transform (transformation formula) exists which has the form

where the integral is taken along any vertical line on a complex plane for a > s0 and is meant as the main Cauchy value. Some of the properties of the Laplace transform are:
Passage to the limit

Linearity: for any constant α and β

where f and g are the originals and F and Q are the respective transforms.
Transform of a derivative

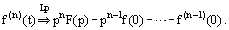
Differentiation of a transform
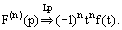
Transformation of an integral

Integration of a transform
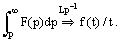
Time-shift theorem
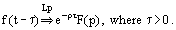
Frequency-shift theorem

Convolution theorem

These, and a number of other properties of the Laplace transform formulated as theorems and their corollaries, make up the body of the Laplace transform method.
Among other integral transforms related to the Laplace transform, and used in solving problems of mathematical physics by the operational method, are the Fourier transform, Mellin's transform, Hankel's transform (for cylindrical geometry) etc.
The operational methods (the Laplace transform or related methods) are especially useful in solving ordinary linear differential equations with constant coefficients and systems of such equations.
The method can also be used in solving integral and integro-differential (Volterra's equations of the first and second kind) equations, and also of problems of mathematical physics described by nonstationary and stationary partial differential equations.