The mass flow rate 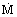 of a free flowing granular material through a circular orifice of diameter D0 in the base of a cylindrical bunker might reasonably be expected to depend on the depth of the material in the bunker H, the diameter of the bunker D, the particle diameter d, the gravitational acceleration g, the density of the material ρ and the coefficient of friction μ.
of a free flowing granular material through a circular orifice of diameter D0 in the base of a cylindrical bunker might reasonably be expected to depend on the depth of the material in the bunker H, the diameter of the bunker D, the particle diameter d, the gravitational acceleration g, the density of the material ρ and the coefficient of friction μ.
Thus

For a conical or wedge-shaped , the half angle α replaces the bunker diameter D.
It is found experimentally that neither the bunker diameter D nor the quantity of material in the bunker, as typified by the height H, has any significant effect on the flow rate. There are good theoretical reasons for both these observations as described by Nedderman (1993) and Nedderman et al. (1982) among many others. It is also found that, provided d << D0, the effect of particle diameter is slight. Ignoring, therefore, the effects of H, D and d, dimensional analysis shows that the only permissible form is that

Early workers did not find the exponent of 5/2 on D0, but Beverloo et al. (1962), plotting  vs. D0, found a linear relationship but with an intercept which was proportional to the particle diameter d. They produced what is known as the Beverloo correlation,
vs. D0, found a linear relationship but with an intercept which was proportional to the particle diameter d. They produced what is known as the Beverloo correlation,

where C is roughly 0.58 but depends to some slight extent on the coefficient of friction. Grace and Raffle (1986) report a value as large as 0.64 for glass spheres. The parameter k depends on the particle shape, but takes a value close to 1.5 for spherical particles. It is of interest to note that Hagen devised a similar correlation some 100 years earlier, but this seem to have been forgotten in the interim.
It is important to use the correct density in Eq. (3) and in similar correlations given below. The density of a granular material can be varied by compaction over a considerable range. However, experiments show that the mass flow rate is independent of the initial degree of compaction of the material. It appears that on initiation of discharge the material dilates to some density characteristic of the flowing material and it is this density that must be used in these correlations. This density seems to be close to the lowest stable density and can be measured by gently filling a container of known volume.
If the orifice is too small, particles may wedge in it, causing intermittent flow or even complete stoppage. Equation (3) should only be used if D0 > 6d, and in this range the correction kd can never be a significant parameter.
The fact that the effective orifice diameter is (D0 – kd) is often called the empty annulus effect, since it seems to suggest that no particles pass through an annular zone of width 1/2kd. There is in fact no such empty annulus. Instead those particles near the edge of the orifice seem to be retarded by some process that is not yet fully understood.
For noncircular orifices the flow rate seems to be proportional to the group A*√DH, where the hydraulic mean diameter DH is defined as 4A*/P* and A* and P* are the area and perimeter of the region remaining after an "empty annulus" of 1/2kd has been removed from the orifice. Casting Eq. (3) into this form gives,
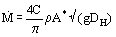
For a long slot orifice of length L and width B (B << L) Eq. (4) becomes,

or, taking C = 0.58 and k = 1.5,
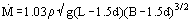
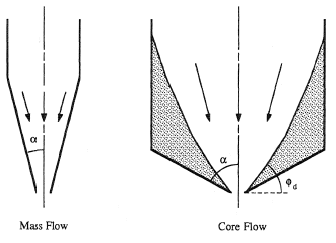
A pre-Beverloo correlation by Rose and Tanaka (1959) gives the effect of hopper angle on the mass flow rate. The flow pattern in a discharging hopper can be classified as either mass or core flow. In mass flow all the material is in motion, whereas in core flow there exists a comparatively narrow flow channel between stagnant zones. We will denote the angle between the lower end of the stagnant zone boundary and the horizontal by 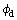 as shown in Figure 1.
as shown in Figure 1.
Mass flow occurs in comparatively narrow hoppers whereas core flow occurs in wide-angled hoppers and cylindrical bunkers. Within core flow the mass flow rate is independent of the hopper angle and is therefore given by Eq. (3). Within mass flow, the mass flow rate is a function of the hopper angle and Rose and Tanaka give the multiplicative factor (tan α tan 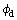 )–0.35. Incorporating this idea into the Beverloo correlation gives,
)–0.35. Incorporating this idea into the Beverloo correlation gives,

where

Unfortunately it is not easy to predict the value of 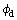 and a value of 45° is recommended by the Draft British Code of Practice for Silo Design [BMHB (1987)] in the absence of more reliable information.
and a value of 45° is recommended by the Draft British Code of Practice for Silo Design [BMHB (1987)] in the absence of more reliable information.
It is seen that none of the correlations above contains any parameter which can easily be varied to control the flow rate. Only the orifice size can be used for this purpose, necessitating the use of a slide valve with the inevitable risk of jamming. Instead, the flow can be varied by injecting air into the hopper, giving a gauge pressure ΔP above the material. The absence of any term involving H in the Beverloo correlation shows that the mass flow rate is determined by conditions in the immediate vicinity of the orifice. If this is so, we can argue that in gravity flow the material is driven by its own weight pg, but in air-augmented flow it is driven by the sum of its own weight and the pressure gradient at the orifice (dp/dr)0 Thus one might expect to replace the term √g in the Beverloo correlation by √(g + (dp/dr)0/ρ) giving
The pressure gradient can be found from consideration of the percolation of air through the material and if the gas Reynolds number is low enough, Darcy's Law can be used, giving (dp/dr)0 = ΔP/r0, where r0 is the radius from the virtual apex to the edge of the orifice, i.e., D0 = 2r0 cos α. In this case,

The results for higher Reynolds numbers are given by Thorpe (1984) and Nedderman, Tüzün and Thorpe (1983).
If a material is discharged from an unventilated hopper, air will have to enter through the orifice countercurrent to the discharging material. This will set up an adverse pressure gradient, causing a reduction in the mass flow rate. This can easily be evaluated from Equation (9) if the permeability of the material is known.
The Beverloo correlation, and its modified forms given above are valid for coarse cohesionless materials. For cohesive materials, the flow rate tends to be irregular and unreproducible. This is because the cohesion is very sensitive to the previous treatment of the material and furthermore tends to increase during storage. Thus a material which flows reliably immediately after filling a hopper may flow irregularly, or not at all, after some period of storage.
Fine particles discharge at rates less than those predicted by the Beverloo correlation, even if cohesionless. The reason for this is that all materials dilate to some extend as they approach the orifice. Thus there must be relative motion between the material and the interstitial fluid. If the permeability is low, this will set up an adverse pressure gradient that retard the flow. Nonetheless such materials obey a modified form of the Beverloo correlation but with lower values of the parameter C. Verghese (1993) proposes the correlation,

where d is measured in mm, but this correlation has been tested on a very limited range of materials and should therefore be used with caution.
REFERENCES
Beverloo, W. A., Leniger, H. A. and Van de Velde, J. (1961), The flow of granular solids through orifices Chem. Eng. Sci. 15, 260. DOI: 10.1016/0009-2509(61)85030-6
BMHB (1987) Silos; Draft Design Code.
Grace, S. M. and Raffle, M. N. (1986) Dept. of Chem. Engng. Part 2 Tripos Report, University of Cambridge.
Nedderman, R. M. (1992) Statics and Kinematics of Granular Materials, CUP.
Nedderman, R. M., Tuzun, U. and Thorpe, R. B. (1983), The effect of interstitial air pressure gradients on the discharge from bins. Pow. Tech., 35, 69. DOI: 10.1016/0032-5910(83)85028-1
Nedderman, R. M., Tuzun, U., Savage, S. B. and Houlsby, G. T. (1982), The flow of granular materials—I : Discharge rates from hoppers Chem. Eng. Sci., 37, 1597. DOI: 10.1016/0009-2509(82)80029-8
Rose, H. F. and Tanaka, T. (1959) The Engineer (London), 208, 465.
Thorpe, R. B. (1984) Ph.D. Thesis, University of Cambridge.
Verghese, T. M. (1992) Ph.D. Thesis, University of Cambridge.
Referencias
- Beverloo, W. A., Leniger, H. A. and Van de Velde, J. (1961), The flow of granular solids through orifices Chem. Eng. Sci. 15, 260. DOI: 10.1016/0009-2509(61)85030-6
- BMHB (1987) Silos; Draft Design Code.
- Grace, S. M. and Raffle, M. N. (1986) Dept. of Chem. Engng. Part 2 Tripos Report, University of Cambridge.
- Nedderman, R. M. (1992) Statics and Kinematics of Granular Materials, CUP. DOI: 10.1002/cite.330660532
- Nedderman, R. M., Tuzun, U. and Thorpe, R. B. (1983), The effect of interstitial air pressure gradients on the discharge from bins. Pow. Tech., 35, 69. DOI: 10.1016/0032-5910(83)85028-1
- Nedderman, R. M., Tuzun, U., Savage, S. B. and Houlsby, G. T. (1982), The flow of granular materials—I : Discharge rates from hoppers Chem. Eng. Sci., 37, 1597. DOI: 10.1016/0009-2509(82)80029-8
- Rose, H. F. and Tanaka, T. (1959) The Engineer (London), 208, 465.
- Thorpe, R. B. (1984) Ph.D. Thesis, University of Cambridge.
- Verghese, T. M. (1992) Ph.D. Thesis, University of Cambridge.