The process of Mass Transfer across an interface, or across a virtual surface in the bulk of a phase, is the result of a chemical potential driving force. This driving force is more usually expressed in terms of Concentrations of the species, or Partial Pressures in the case of gas phases. The rate of transfer of a given species per unit area normal to the surface, i.e., the species flux, depends on some of the physical properties of the system and on the degree of Turbulence of the phases involved. In general the relationship between the flux and these parameters is not easily developed from fundamentals of mass transfer, so that mass transfer coefficients have been defined that lump them all together. These definitions are of the form:
Flux = coefficient.(concentration difference) .
In the case of species crossing an interface, there are several expressions for the flux based on different driving forces. The interfacial flux,
 , can be expressed in the four following ways depending on the concentration driving force used:
, can be expressed in the four following ways depending on the concentration driving force used:
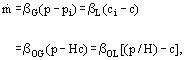
where
 is the mass flux; β, the mass transfer coefficient; and the subscripts L and G indicate the gas and liquid phases. The first two equations define the single-phase gas and liquid mass transfer coefficients. Since the interfacial concentrations pi and ci are usually unknown, the overall mass transfer coefficients βOG and βOL defined by the two last equations, are more commonly used, in these equations H is the equilibrium distribution coefficient of the solute between the two phases at equilibrium. Since the interfacial flux must be the same irrespective of the driving force used to express it, the four numerical coefficients are different and have different units. This is also the case when dimensionless driving forces, such as molar or mass fractions, are used. The mass transfer coefficients depend on the diffusivity of the solute and the hydrodynamics of the phases. They can be calculated using expressions derived from fundamentals of mass transfer, in the case of laminar flow, or from empirical correlations.
is the mass flux; β, the mass transfer coefficient; and the subscripts L and G indicate the gas and liquid phases. The first two equations define the single-phase gas and liquid mass transfer coefficients. Since the interfacial concentrations pi and ci are usually unknown, the overall mass transfer coefficients βOG and βOL defined by the two last equations, are more commonly used, in these equations H is the equilibrium distribution coefficient of the solute between the two phases at equilibrium. Since the interfacial flux must be the same irrespective of the driving force used to express it, the four numerical coefficients are different and have different units. This is also the case when dimensionless driving forces, such as molar or mass fractions, are used. The mass transfer coefficients depend on the diffusivity of the solute and the hydrodynamics of the phases. They can be calculated using expressions derived from fundamentals of mass transfer, in the case of laminar flow, or from empirical correlations.
REFERENCES
Skelland, A. H. P. (1974) Diffusional Mass Transfer. John Wiley.
Verweise
- Skelland, A. H. P. (1974) Diffusional Mass Transfer. John Wiley.