Conduction is a diffusion process by which thermal energy spreads from hotter regions to cooler regions of a solid or stationary fluid. A range of microscopic diffusive mechanisms may be involved in heat conduction (Gebhart (1993)) and the observed overall effect may be the sum of several individual effects, such as molecular diffusion, electron diffusion and lattice vibration.
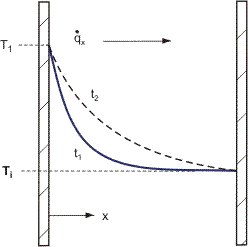
A simple model of the mechanism of heat conduction is provided by the Kinetic Theory of Gases. Consider the system consisting of a stationary mass of an ideal monatomic gas confined between two parallel isothermal walls in a zero gravity field (i.e., no natural convection possible) and initially at a uniform temperature Ti throughout, as illustrated in Figure 1.
Suppose that at time t = 0, the left hand wall is raised to and kept at a higher temperature T1 so that at some subsequent time, t1, a typical temperature distribution such as that represented by the full curve develops, indicating a spread of heat from the hot wall in the direction of the cold wall. This energy transfer process in a simple gas is the result of the diffusive effects of random molecular motion. Consider the molecular traffic across a vertical plane, such as that represented by the vertical dashed line in Figure 1. Because of the random nature of molecular motion and because there can be no bulk flow of gas, molecules must cross the imaginary plane at an equal rate in both the positive and negative x-directions. Those molecules crossing the plane in the positive x-direction possess more translational/rotational/vibrational energy than those crossing in the opposite direction. Molecular collisions lead to energy transfer from more energetic molecules to less energetic ones. By this diffusive action, the thermal wave strengthens and advances so that at some later time, t2, the temperature distribution has evolved as indicated by the broken curve in Figure 1.
Energy diffusion in more complex fluids and solids is not so mechanistically simple, but whatever the actual mechanism of energy transport at a microscopic level, a macroscopic formulation of the rate process of diffusion, known as Fourier’s Law, provides a simple mathematical description and is crucial for the analysis of conduction problems. The differential form of Fourier’s Law for one-dimensional conduction in an isotropic medium with constant thermal conductivity, such as the process represented in Figure 1 is:

where it is clear that for the most part  varies with x and t until steady-state is approached (t → ∞), whereupon
varies with x and t until steady-state is approached (t → ∞), whereupon  becomes constant with both x and t and the temperature distribution becomes linear.
becomes constant with both x and t and the temperature distribution becomes linear.
Many practical conduction problems are of the undeveloped or unsteady-state type, with the fully-developed solution forming a simple limiting case. Typically, a conduction problem will be posed in the form of a specified geometry, an initial temperature distribution throughout the region of interest, and information on external and internal heating effects. The normal requirement will be for information on the temperature distribution at some elapsed time from the commencement of the heating or cooling process. The starting point for the analysis of such a problem is the differential form of the general conduction equation, which is derived by applying the principle of conservation of energy to a representative differential control volume, such as the one illustrated in Figure 2.
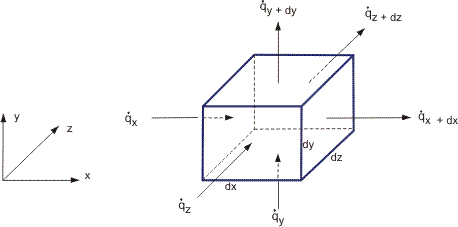
Figure 2. Cartesian differential control volume used to formulate an energy balance for a general conduction process.
The control volume (dxdydz) is drawn in the rectangular Cartesian coordinate system, but could equally well be drawn in the cylindrical or polar coordinate systems [see Bird, Stewart and Lightfoot (I960)]. The control volume is embedded in a system which exemplifies the most general case of conduction, i.e., unsteady three-dimensional conduction in a material which may be consuming or producing thermal energy internally by virtue of some process, such as endothermic chemical reaction or ohmic heating. The volumetric rate of any such internal energy conversion will be denoted by  .
.
The only way that energy can pass into or out of the control volume across the six imaginary faces is by the process of conduction. An energy balance on the control mass in the control volume can be written as:
Net rate of energy gain by conduction + Rate of energy production/loss by internal processes = Rate of energy increase/decrease of control mass.
Each of these terms can be quantified to produce a differential energy balance, as follows:
(1) The net rate of energy gain (loss) by conduction in the x-direction is  . The typical parabolic temperature profile associated with the transient conduction process illustrated in Figure 1 indicates that the local heat flux
. The typical parabolic temperature profile associated with the transient conduction process illustrated in Figure 1 indicates that the local heat flux  is a function of x (see Fourier’s Law) and so a Taylor Series expansion can be used to approximate
is a function of x (see Fourier’s Law) and so a Taylor Series expansion can be used to approximate  :
:

Accounting for the energy gains due to conduction in the y and z directions gives the total net rate of energy gain by the control mass to be:

This expression can be rewritten with T as the dependent variable by using Fourier’s Law to substitute for 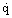 :
:

If it is assumed that λ is invariant with T (a reasonable assumption in many cases where the temperature changes are not large, see Thermal Conductivity), then the conduction term in the energy balance simplifies to:

(2) The second term in the energy balance which accounts for the rate of energy gain or loss in the control volume due to possible internal energy conversion processes is simply written as  (dxdydz).
(dxdydz).
(3) The third term in the energy balance is the rate at which the control mass stores energy as a net result of conduction and internal energy conversion, which is quantified as: mass × specific heat × rate of rise of temperature, or,

The complete energy balance can now be written as:

or, simplifying:

This energy balance often appears in vector form:

where the operator  2, known as the Laplacian, may also be expressed in cylindrical or spherical coordinates. This is the conduction equation and is one of the most important in applied mathematics. It is the simplest approximation to bulk processes governed at the microscopic level by random spatial variations.
2, known as the Laplacian, may also be expressed in cylindrical or spherical coordinates. This is the conduction equation and is one of the most important in applied mathematics. It is the simplest approximation to bulk processes governed at the microscopic level by random spatial variations.
1. Fourier Equation
For conduction problems in which there is no internal energy conversion, the energy balance simplifies to:

2. Poisson Equation
For steady-state conduction with internal energy conversion, the energy balance may be written as:

3. Laplace Equation
For steady-state conduction with no internal energy conversion, the energy balance reduces to its simplest form:

This is a potential field equation and the analogy with other potential field systems can be utilized to obtain solutions to conduction problems.
The analysis of a conduction problem involves the solution of the appropriate form of the differential energy balance, subject to the boundary conditions applicable to the problem at hand. A well-posed, soluble and general heat conduction problem will have the following characteristics:
It is required to find T(x,y,z,t) such that:
(10)
with 0 < (x, y, z, t) < ∞.
The initial temperature distribution throughout the region of interest is known, i.e., T = Ti (x, y, z) at t = 0, except for steady-state problems and problems where
 or the boundary conditions vary periodically with time.
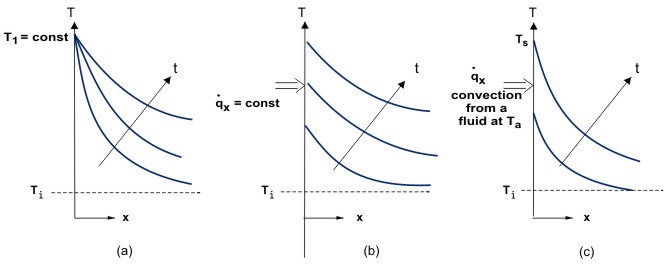
or the boundary conditions vary periodically with time.T must also satisfy two boundary conditions for each coordinate, which are often of the following three common types (see Figure 1):
(1) Boundary conditions of the first kind (or Dirichlet conditions) where T is specified around the edge of the conduction domain for t > 0, e.g., T = T1 at x = 0, as indicated in Figure 3a.
(2) Boundary conditions of the second kind (or Neumann conditions) where the gradient of T normal to the boundary is specified around the boundary of the solution domain for t > 0. A common example is a surface which is subjected to a constant heat flux, i.e.,  , this situation being represented in Figure 3b.
, this situation being represented in Figure 3b.
(3) Boundary conditions of the third kind where the gradient of T normal to the boundary is directly proportional to the temperature on the boundary, as is the case when convection occurs at the surface. A heat balance at a conduction boundary where the heat flux due to conduction at the edge of the conduction domain (at Ts), which varies with time, is equated to the convective heat flux from the surrounding fluid at Ta, gives  . This boundary condition is represented in Figure 3c.
. This boundary condition is represented in Figure 3c.
Although many problems will have boundary conditions which fall into the above three categories other, more complex boundary conditions can arise, [see for example Carslaw and Jaeger (1980)].
Good introductions to the main features of the most widely-used methods for solving the conduction equation can be found in textbooks, such as that by Kreith and Bohn (1993). Analytical solutions of conduction problems in simple geometric shapes (plates, cylinders and spheres) have been compiled by Carslaw and Jaeger (1980), and many solutions are presented in the form of charts by Schneider (1963), which have considerable utility for estimation and design. A wide range of techniques have been employed to obtain solutions to the conduction equation; the most common ones are clearly described in Hill and Dewynne (1987) and Myers (1987). Numerical techniques have been developed for the solution of heat conduction problems and these numerical methods are capable of dealing with complex geometries and non-linearities such as temperature dependent physical properties, anisotropy and boundary conditions which are nonlinear in T, as when radiative heating/cooling is involved. A list of commercially-available software packages for the numerical solution of a wide range of conduction (and convection) problems is given by Kreith and Bohn (1993). Solution methods suitable for dealing with an important class of transient conduction problems, known as Stefan problems, and involving the additional feature of a moving phase-change boundary (melting or freezing fronts) are described by Crank (1984) and Ockenden and Hodgkins (1975).
REFERENCES
Carslaw, H. S. and Jaeger, J. C. (1980) Conduction of Heat in Solids, 2nd ed., Clarendon Press, Oxford.
Crank, J. (1984) Free and Moving Boundary Problems, Clarendon Press, Oxford.
Hill, J. M. and Dewynne, J. N. (1987) Heat Conduction, Blackwell Scientific Publications, Oxford.
Kreith, F. and Bohn, M. S. (1993) Principles of Heat Transfer, 5th ed., West Publishing Company, St. Paul.
Myers, G. E. (1987) Analytical Methods in Conduction Heat Transfer, Genium Publishing Co., Schenectady, New York.
Ockenden, J. R. and Hodgkins, W. R. (1975) Moving Boundary Problems in Heat Flow and Diffusion, Clarendon Press, Oxford.
Schneider, P. J. (1963) Temperature Response Charts, John Wiley, New York. DOI: 10.1016/0017-9310(63)90057-7
Verweise
- Carslaw, H. S. and Jaeger, J. C. (1980) Conduction of Heat in Solids, 2nd ed., Clarendon Press, Oxford.
- Crank, J. (1984) Free and Moving Boundary Problems, Clarendon Press, Oxford. DOI: 10.1017/S0022112085212750
- Hill, J. M. and Dewynne, J. N. (1987) Heat Conduction, Blackwell Scientific Publications, Oxford.
- Kreith, F. and Bohn, M. S. (1993) Principles of Heat Transfer, 5th ed., West Publishing Company, St. Paul.
- Myers, G. E. (1987) Analytical Methods in Conduction Heat Transfer, Genium Publishing Co., Schenectady, New York.
- Ockenden, J. R. and Hodgkins, W. R. (1975) Moving Boundary Problems in Heat Flow and Diffusion, Clarendon Press, Oxford. DOI: 10.2307/2005415
- Schneider, P. J. (1963) Temperature Response Charts, John Wiley, New York. DOI: 10.1016/0017-9310(63)90057-7