Moisture measurement has found wide use in scientific research and production, and during the past decades many moisture measurement techniques have been introduced, among which the classic combination of Dry and Wet Bulb Thermometers is one of the most convenient and reliable. However, in order to improve its measurement accuracy it is necessary to study the relation between the measured wet bulb temperature Tw and the adiabatic saturation temperature T* of moist air.
The adiabatic saturation temperature is the equilibrium temperature of moist air under adiabatic conditions, and it is very difficult to measure. In practice the wet bulb temperature is often used as a substitute for the adiabatic saturation temperature although the measured wet bulb temperature is quite different from the adiabatic saturation temperature, because it is determined under nonadiabatic conditions.
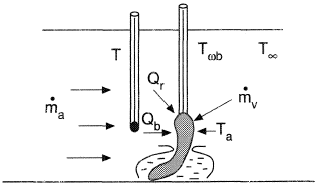
A dry/wet bulb thermometer is shown in Figure 1. When moist air flows along the wet bulb surface, a very thin boundary layer of saturated most air forms around it. The airstream (with a mass flow
 ) flowing near the saturated boundary layer will absorb a certain amount of vapor (with a mass flow mv) diffusing from the saturated layer. Because of insufficient heat and mass exchange the airflow cannot reach the saturated state and it will have a temperature higher than the wet bulb temperature. Since there is heat and mass exchange between the boundary layer and the airflow, the temperature in the saturated boundary layer cannot be treated as the adiabatic saturation temperature; that is, the measured wet bulb temperature is not the adiabatic saturated temperature. The measured wet bulb temperature is affected by air velocity, wet bulb diameter, the heat exchange with surroundings and the thermal state of the moist air.
) flowing near the saturated boundary layer will absorb a certain amount of vapor (with a mass flow mv) diffusing from the saturated layer. Because of insufficient heat and mass exchange the airflow cannot reach the saturated state and it will have a temperature higher than the wet bulb temperature. Since there is heat and mass exchange between the boundary layer and the airflow, the temperature in the saturated boundary layer cannot be treated as the adiabatic saturation temperature; that is, the measured wet bulb temperature is not the adiabatic saturated temperature. The measured wet bulb temperature is affected by air velocity, wet bulb diameter, the heat exchange with surroundings and the thermal state of the moist air.
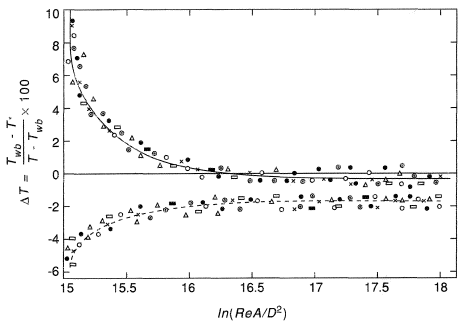
Experiments [Zhao Yuzhen (1992)] have been conducted under the following conditions: dry bulb temperature from 16°C to 88.3°C; air velocity from 0 to 40 m/s, and wet bulb diameters of 6, 8, 10, 11 and 12 mm. The experimental curves are shown in Figure 2. For the unshielded dry/wet bulb thermometer, the relative deviation, (Twb — T*)/(T — Twb), is shown with a solid curve drawn through the data points. For the shielded dry/wet bulb thermometer data are also plotted in Figure 2 and correlated with the dashed curve. It can be seen that for the unshielded wet bulb, as ln (ReA/D2) increases Twb tends to T*; at ln (ReA/D2) = 16.2, the deviation is zero, that is Twb = T*, and when ln (ReA/D2) > 16.5, the deviation becomes constant.
The explanation of this phenomenon is as follows. When ln (ReA/D2) is comparatively small, the evaporating vapor is transferred mainly by the pressure difference of vapor in the boundary layer, so it spreads slowly. For the unshielded wet bulb thermometer, the latent heat of vaporization of water at the wet bulb is supplied through radiation as well as convection, so the partial pressure and the corresponding saturation temperature of the vapor around the wet bulb are higher, thus resulting in the wet bulb temperature being higher than the adiabatic saturated temperature. When ln (ReA/D2) increases, the vapor diffusion not only depends on the pressure differences, but also upon the influence of the flow, so the partial pressure of the vapor around the wet bulb falls, and its saturated temperature becomes lower and tends to the adiabatic saturated temperature. If ln (ReA/D2) > 16.2 vapor is removed instantly by flowing air, the partial pressure of vapor around the wet bulb remains stable and so does the wet bulb temperature. It can be seen from Figure 2 that for an unshielded wet bulb, when ln (ReA/D2) > 16, the wet bulb temperature is much closer to the adiabatic saturated temperature.
From the solid line in Figure 2. the following expression is obtained in which the dependence of the relative deviation on Re and wet bulb diameter D is correlated as:

Zhao Yuzhen (1991) recommended a correlation for the following conditions: dry bulb temperature at 5 ~ -15°C; wind velocity varied from 0 to 40 m/s and wet bulb diameters of 2, 5,6, 7, 5, 8 mm.

James L. Threlkeld (1970) obtained two correlations: when the dry bulb temperature equals that of the surroundings, the relative deviation (Twb - T*)/(T - Twb) is:

For the shielded dry/wet bulb thermometer the following formula is employed:

where
hr = radiation heat transfer coefficient
hc = convection heat transfer coefficient
B = coefficient of wet bulb
k* =
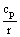 .
.
Kent (1985) recommends a new type dry/wet bulb thermometer, which can be used for the measurement of high temperature moist air. With dry bulb temperature 200°C and wet bulb temperature 99°C and an uncertainty of less than 2% is claimed.
REFERENCES
Threlkeld, J. L. (1970) Thermal Environmental Engineering 2nd edn., Prentice-Hall, Englewood Cliffs, N.J.
Kent, A. C. (1985) An Aspirated Humidity and Energy Meter for High Temperature Moist Air. Proceedings of Moisture and Humidity.
Zhao Yuzhen and Jiang Baocheng (1992) Experimental Study of the Effects of Wind Speed, Radiation and Wet Bulb Diameter on Wet Bulb Temperature. Experimental Thermal and Science. DOI: 10.1016/0894-1777(92)90122-L
Zhao Yuzhen and Jiang Baocheng (1991) The Influence on Wet Bulb Temperature of Wind Velocity, Radiation and Wet Bulb Diameter at Low Temperature. Journal of Engineering Thennophysics of China.
References
- Threlkeld, J. L. (1970) Thermal Environmental Engineering 2nd edn., Prentice-Hall, Englewood Cliffs, N.J.
- Kent, A. C. (1985) An Aspirated Humidity and Energy Meter for High Temperature Moist Air. Proceedings of Moisture and Humidity.
- Zhao Yuzhen and Jiang Baocheng (1992) Experimental Study of the Effects of Wind Speed, Radiation and Wet Bulb Diameter on Wet Bulb Temperature. Experimental Thermal and Science. DOI: 10.1016/0894-1777(92)90122-L
- Zhao Yuzhen and Jiang Baocheng (1991) The Influence on Wet Bulb Temperature of Wind Velocity, Radiation and Wet Bulb Diameter at Low Temperature. Journal of Engineering Thennophysics of China.