In kinetic theory, the mean free path is defined as the mean distance travelled by a molecule between collision with any other molecule. For a dilute gas composed of hard spherical molecules of kinds A and B, the mean time τAB between successive collisions of a given A molecule with B molecules is given by
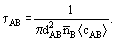
Here, dAB is the mean diameter of molecules A and B,
 is the number density of B molecules, and
is the number density of B molecules, and
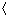 cAB
cAB is the mean relative speed of molecules A and B. According to the Maxwell-Boltzmann velocity distribution law, molecular velocities are not correlated and
is the mean relative speed of molecules A and B. According to the Maxwell-Boltzmann velocity distribution law, molecular velocities are not correlated and
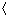 cAB
cAB is therefore given in terms of the mean speeds of the individual molecules by
is therefore given in terms of the mean speeds of the individual molecules by
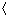 cAB
cAB =
=
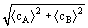 where, for molecules of type i with mass mi,
where, for molecules of type i with mass mi,
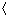 ci
ci = (8kT/πmi)1/2, where k is Boltzmann's constant and T is the absolute temperature.
= (8kT/πmi)1/2, where k is Boltzmann's constant and T is the absolute temperature.
The mean free path lAB travelled by a given A molecule between successive collisions with B molecules is simply
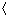 cA
cA τAB or
τAB or

Real molecules interact through intermolecular forces which vary smoothly with distance. Consequently, there is no unique counterpart of the hard-sphere collision cross-section
 and no unique definition of what constitutes a collision. Often, dAB is replaced by the separation σAB at which the A-B intermolecular potential energy crosses zero. Alternatively, dAB may be determined from viscosity data by comparison with the theoretical predictions for hard spheres [Kennard (1938)]. These formulas are easily specialized to the case where A and B are identical and, if d is estimated from viscosity data, then
and no unique definition of what constitutes a collision. Often, dAB is replaced by the separation σAB at which the A-B intermolecular potential energy crosses zero. Alternatively, dAB may be determined from viscosity data by comparison with the theoretical predictions for hard spheres [Kennard (1938)]. These formulas are easily specialized to the case where A and B are identical and, if d is estimated from viscosity data, then
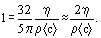
where η is viscosity and ρ density.
REFERENCES
Kennard, E. H. (1938) Kinetic Theory of Gases. McGraw-Hill. New York.
References
- Kennard, E. H. (1938) Kinetic Theory of Gases. McGraw-Hill. New York.