The distribution of molecular velocities in a gas, established first by Maxwell and later proved rigorously by Boltzmann, is given by a function F and is today known as the Maxwell-Boltzmann velocity distribution function. Since this probability function depends upon the specified velocity u, F = F(u) and is defined such that F(u) dudvdw gives the probability that a molecule selected at random will, at any instant, have a velocity u with Cartesian components in the ranges u to u + du, v to v + dv, and w to w + dw.
The Maxwell-Boltzmann velocity distribution function refers specifically to a gas which is at rest (in the sense that no macroscopic flow exists) and in a state of thermodynamic equilibrium. Subject to these assumptions, the distribution law states that

where m is the mass of one molecule, k is Boltzmann's constant, and c = |u| is the speed of the molecule. Note that F is given as the product f(u)f(v)f(w) and that the velocity components in different directions are therefore uncorrelated. In other words, the probability of the molecule possessing a specified velocity u in the x direction is not influenced by the values of v and w for that or any other molecule. The function f is thus a velocity distribution function for motion in a specified direction, and is given by

where q represents one of (u,v,w).
The distribution function Fc(c) for molecular speed, irrespective of direction, is easily found by:

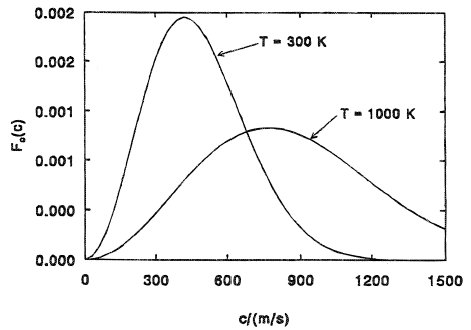
The behavior of the function Fc(c) is illustrated in Figure 1 for nitrogen gas at temperatures of 300 K and 1000 K. Note that f and Fc are normalized distribution functions which, upon integration with respect to their argument on [0, ∞], yield unity. Various 'average' molecular speeds may be obtained easily from the distribution function Fc as follows:
| The most probable speed (maximum Fc): | ĉ = (2kT/m)1/2 |
| The mean speed: | 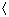 c
c
 =
=
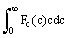 = (8kT/πm)1/2
= (8kT/πm)1/2 |
| The root-mean-square speed: |  = (
= (
 )1/2 = (3kT/m)1/2
)1/2 = (3kT/m)1/2 |
These measures of average speed may be compared with the speed of sound in the perfect gas: (kTγ/m)1/2. For nitrogen at 300 K, the speed of sound is 353 m/s; ĉ = 420 m/s,
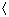 c
c
 = 478 m/s; and
= 478 m/s; and
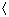 c2
c2 1/2 = 516 m/s: all are proportional to
1/2 = 516 m/s: all are proportional to
 .
.
REFERENCES
Kennard, E. H. (1938) Kinetic Theory of Gases. McGraw-Hill. New York.
References
- Kennard, E. H. (1938) Kinetic Theory of Gases. McGraw-Hill. New York.