The Legendre polynomial series is the decomposition of a function f(x) square integrable on the interval (−1, 1) into a series according to the Legendre polynomial system Pn(x) n = 0, 1,
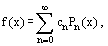
the coefficients of series cn are calculated by:

The Legendre polynomial system is orthogonal to weight 1 and is complete on the interval (−1, 1).
The orthogonality relationships for Legendre polynomials have the form


Therefore, the Legendre polynomial series is a type of Fourier Series written in the system of orthogonal polynomials. The partial sums of a Legendre series bring the functions f(x) closer in the sense of a root-mean-square deviation and the condition limn→ ∞ cn = 0 is satisfied.
The Fourier series, written in the form of Legendre polynomials within the interval (−1, 1), is similar to the trigonometric Fourier series: convergence of both series takes place, which means that a Fourier-Legendre function f(x) converges at the points x 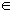 (−1, 1) when a trigonometric series of a Fourier function F(θ) =
(−1, 1) when a trigonometric series of a Fourier function F(θ) =  f(cos θ) converges at the point θ = arcsin x.
f(cos θ) converges at the point θ = arcsin x.
Near the ends of the orthogonality interval, the properties of the Fourier and Legendre series are different since at points x 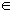 (−1, 1), the orthonormal Legendre polynomials increase infinitely.
(−1, 1), the orthonormal Legendre polynomials increase infinitely.
If a function f(x) on the interval (−1, 1) is continuous and satisfies a Lipschitz condition, then the Fourier and Legendre series converges to a function uniformly over the interval (−1, 1).
The expansion in terms of a complete orthogonal system of adjoint Legendre functions  (x),
(x),  , …,
, …,  (x) also plays an important part in problems of radiation heat transfer.
(x) also plays an important part in problems of radiation heat transfer.