The effect produced by the superposition of two or more waves is called interference. Interference appears in the case of temporally and spatially coherent waves. Therefore, waves which are able to interfere have to be generated by a monochromatic, point light source (for example, lasers). Generation by means of separate light sources is not possible i.e., the light waves have to be generated by splitting up a single beam into two separate light waves. After passing along different optical paths, their superposition causes an interference pattern.
Originated by a single light source, waves have a limited connected length known as the coherent length. The coherent length is directly connected to the monochromatic quality of the light. As a result of the beam splitting, the light is subject to a path change. However, to obtain interference the path change must be smaller than the coherent length. Below, a description of Dual Beam Interferometry is provided.
Each of the two waves is precisely described by their amplitude and phase distribution. Both waves have different amplitudes and a constant temporal phase shift. To record the phase shift the phenomenon of interference is used. As a result of the phase shift a visible and recordable brightness and darkness distribution is created. Recorded in this way, the difference of the phase angle corresponds to a local difference of the optical paths. Due to the dependency of the interference effect on the ratio of path difference Δ(n·d) to wave length λ, it is possible to use interferometry for determining path d (measurement of length), refraction n (refractometry) and wave length λ (spectroscopy), or to examine the modifications of these parameters.
In the field of heat and mass transfer, interferometry is mainly used for the determination of refraction fields which—due to their-physical dependency—can later be converted into density, temperature or concentration fields [Ladenburg (1954)].
The whole information about a phase influencing object (for example, a thermal boundary layer) is given by the distortion of an originally plane wavefront. Its structure can be made visible by one of the interference methods. Phase differences in a distorted wavefront relating to a reference wavefront cause changes in the intensity of light whereby they become visible. Two of the most important techniques used to generate interference are described below.
Normal dual beam interference (Mach-Zehnder). Figure 1 shows the interference pattern of natural, convective air cooling of printed circuit boards (PCBs) in a closed casing. An unstable thermal boundary layer exists at the cold top-wall of the casing, which interacts with the air flow rising up from the channels between the PCBs. It produces vortex flow and temperature oscillation. Interference lines are generated if the optical paths n·1 of the reference and object beams differ in multiples S of the wave length λ. Maximum intensity occurs when S is an integer, whereas minimum intensity is caused by path lengths which are odd multiples of λ/2. From this, the refraction differences Δn along a test section 1 can be determined:

![Holographic interferogram of natural convective air cooling in a closed casing with five heated plates [Mayinger (1994)].](/content/5301/InteF1.gif)
Figure 1. Holographic interferogram of natural convective air cooling in a closed casing with five heated plates [Mayinger (1994)].
In the example illustrated in Figure 1 the refraction index within the test section was influenced only by changes in temperature. As first approximation the interference lines can be interpreted as a representing important differences in temperature, and with constant reference conditions as isotherms.

Differential interference. During this process instead of a plane reference wavefront, the same distorted wavefront is used; however, with a lateral shift. In the differential interferometer, measurement and reference waves pass the measurement field with a laterally-shifted distance y and interfere afterwards. This shifting y is known in terms of its amount and direction. The interference lines provide a scale for the gradient of the distorted wavefront. As in the case of normal interference, the phase difference is proportional to the temperature difference so that ΔT/Δy can be measured directly. Heat transfer experiments in particular require knowledge of the temperature gradient dT/dy, and differential interferometry has proved to be a suitable method [Merzkirch (1987)]. In general, however, the accuracy of this measurement method is lower than that obtained with normal dual beam interference.
In an interferometer the measuring and reference beams are generated by splitting one beam of a single light source, nowadays usually a laser. A classification can be made according to the beam splitting method used. Some types are listed below.
a. Amplitude splitting. Classical mirror-interferometers use semipermeable layers (mirrors) as beam-splitting elements. Usual measuring beam diameters (0.1 to 0.3 m) require large and expensive interferometer mirrors with high surface quality.
Examples are the Mach-Zehnder Interferometer, which is suitable for transparent objects. It consists of two beam-splitting and two reflecting mirrors in a rectangle or parallelogram arrangement (Figure 2a). Furthermore, it is suitable for long models (4m) and investigation of temperature fields.
The Jamin Interferometer consists of two sloped mirrors whereby each mirror takes over the functions of beam splitting as well as beam reunification (Figure 2b). The shift between the measuring and reference beam is small. It can be used as a differential interferometer, but is also suitable for measuring refractive indices of gases.
The best known mirror-interferometer is the Michelson Interferometer. It is mainly used for measuring lengths and examining surfaces (Figure 2c). Furthermore, it is not suitable for measuring refractive indices of gases and liquids.
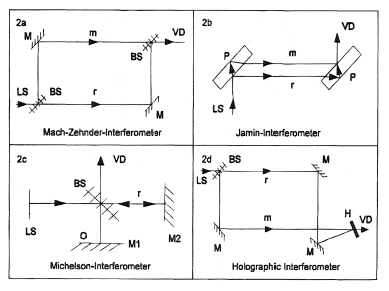
Figure 2. Different types of dual-beam interferometers.LS = light source, M = mirror, BS = beam splitter, VD = view direction, H = hologram, P = plane plate, O = object, m = measuring beam, r = reference beam.
b. Splitting of the wavefront. Lord Rayleigh developed a procedure to determine the refractive index by means of a path-shift compensating arrangement. This procedure has found widespread use in the field of measuring concentrations of two- and three- component mixtures of gases and liquids.
c. Interference-holography. The use of lasers with large coherent lengths as light sources in optical systems opened a wide field of application for holography. The possibility of storing the phase distribution of a light wave and reconstructing it later by means of holography led to several new interference techniques. An object wave can be stored on a hologram, later on released by illumination with the reference beam and superimposed on the present object wave. Thus, two waves passing the measuring object at different times interfere with each other so that the difference of comparison and measuring wave can be measured directly. In the field of transillumination interferometry, the Mach-Zehnder- and the Michelson-Interferometer have been displaced by the Holographic Interferometer (Figure 2d) which offers the advantage of largely eliminating imperfections in the optical components. Not only is it much cheaper to use, but it is also much easier and convenient to handle.
The characteristics of a real implementation of interferometry are discussed below by means of an idealized dual beam interferometer and an idealized phase object. In general, the real qualities are obtained by adding correction terms. In the case of an ideal interferometry the following assumptions, applicable to all types of interferometer,2 are made:
Strictly monochromatic light source: The light source is point shaped and is the origin of undamped spherical wavefronts, which are transformed into plane parallel wavefronts by the use of an ideal lens.
No aberration: The beam paths of the interferometer contain no optical elements at all—particularly the phase influencing object included—which can cause a deflection of the beams (aberration). The beams remain parallel during their passage through the object and no distortion is caused by the projection process.
Interferometer equations in the case of ideal interferometry: In the interference pattern the difference Si·λ of the optical paths at each point P(xi, yi) of the beam cross-section is recorded. The modification of the optical path length of the measuring beam nm(xi, yi)·1 through the test section, compared to the optical path length nr(xi, yi)·1 of the corresponding reference beam (obtained by two-dimensional measuring methods, integrated along the path through the model) is:
The locations of a constant phase difference Si in a two-dimensional object are, for example, points with a constant temperature difference ΔTi = T (xi, yi) − Tref, if the gradient of the refractive index dn/dT is assumed to be constant. Consequently, an interference pattern can be considered as a field of isotherms and the interpretation requires at least the temperature Tref of one point of the cross-section.
Interferometry is frequently used in heat and mass transfer. Figure 3 shows the interferogram of a tube bundle, where the change from laminar to turbulent flow occurs. Fluctuations in the boundary layer can be clearly seen.
The refractive index field can be determined from the interference pattern by Eq. (3). The relation between refractive index n and density ρ is given by the Lorentz-Lorenz equation, which can be simplified for gases (n ≈ 1) to the Gladstone-Dale equation:

Here, N is the molecular refractivity (property constant) and M is the molecular weight. Including the equation of state for ideal gases, Equations (3) and (4) result in:

If the temperature Tref is known at any location, a specific temperature could be assigned to each interference line. If air is used as test fluid the temperature difference between two lines is only a few degrees. In the case of liquids, a linear dependency of the refractive index on temperature is usually assumed. So Equation (3) can be transformed into:
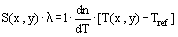
Refractive indices of gases and liquids are listed in Table 1 The sensitivity of interferometric methods for water is 100 times greater than for air.
With Equation (7), the heat transfer coefficient α is calculated from the temperature gradient at the wall (dT/dy)w, determined from the temperature profile T(y) and the temperature difference Tw − T∞:
The interference lines in Figure 3 are isotherms with a temperature difference of 2−3 K. The fringe density at the wall is proportional to the temperature gradient and hence, to the heat transfer coefficient. Therefore, the local Nusselt Number distribution can be estimated directly from the interference pattern. The evaluation of the interferogram in Figure 3 is also presented as the ratio of local and average Nusselt number for different Reynolds Numbers.
REFERENCES
Ladenburg, R. (1954) Interferometry, in Physical Measurements in Gas Dynamics and Combustion. A3. Princeton Univ. Press. Princeton, New Jersey.
Mayinger, F. and Panknin, W. (1974) Holography in Heat and Mass Transfer. 5th Int. Heat Transfer Conference. Tokyo.
Mayinger, F. and Wang, Z. (1994) Experiments on natural convective air cooling of a PCBs array in a closed casing with inclination; Kakaç, S., Yiinchli, H. and Hijikata, K. (1994) Proc. of the NATO Adv. Study Inst. on Cooling of Electr. Systems. Kluwer Academic Publishers.
Merzkirch, W. (1987) Flow Visualization. Academic Press. 2nd edn. Orlando.
Tolansky, S. (1955) An Introduction of Interferometry. McGraw-Hill. New York.
References
- Ladenburg, R. (1954) Interferometry, in Physical Measurements in Gas Dynamics and Combustion. A3. Princeton Univ. Press. Princeton, New Jersey.
- Mayinger, F. and Panknin, W. (1974) Holography in Heat and Mass Transfer. 5th Int. Heat Transfer Conference. Tokyo.
- Mayinger, F. and Wang, Z. (1994) Experiments on natural convective air cooling of a PCBs array in a closed casing with inclination; Kakaç, S., Yiinchli, H. and Hijikata, K. (1994) Proc. of the NATO Adv. Study Inst. on Cooling of Electr. Systems. Kluwer Academic Publishers.
- Merzkirch, W. (1987) Flow Visualization. Academic Press. 2nd edn. Orlando.
- Tolansky, S. (1955) An Introduction of Interferometry. McGraw-Hill. New York.

![Temperature field between three heated tubes with coaxial flow [Mayinger (1974)].](/content/5301/InteF3.gif)

