An integro-differential equation is a mathematical expression which contains derivatives of the required function and its integral transforms. Such equations are typical of those processes where a quantity of interest (a required function) at each point is not unambiguously determined by its value near the point—as on processes described by differential equations—but also depends on the function distribution all over the domain. For instance, a radiation energy intensity along the ray 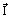 in the emitting, absorbing and scattering medium (I
in the emitting, absorbing and scattering medium (I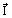 ) is described by an integro-differential equation of radiation transfer, having the form
) is described by an integro-differential equation of radiation transfer, having the form

where Ka, Ks are the absorbtion and scattering coefficients; Ke = Ka + Ks is the attenuation coefficient; and Φ is the scattering phase function. The physical meaning of Eq. (1) is that variation of intensity at a given point along a given direction depends on both the local processes of absorption, scattering (first term on right-hand side) the self-emittance of the medium (second term) and a process of radiation scattering converging to the given point from a whole volume. If only one independent variable is involved in an integro-differential equation, the latter is called an ordinary integro-differential equation. If an integro-differential equation includes derivatives of more than one independent variable, it is called a partial integro-differential equation.
The linear integro-differential equation is a relationship LD(y) + LI(y) = f, where LD is a linear differentiation operator; LI is a linear integration operator such that LD(y1 + y2) = LD(y1) + LD(y2); LI(y1 + y2) = LI(y1) + LI(y2); and f is an arbitrary function of the independent variables. A linear integro-differential equation with partial derivatives of the second order has a differential type of operator. For instance, the equation

belongs to the hyperbolic type if α = 0, β = 1; to the elliptic if α = 0, β = −1; and to the parabolic type if α = 1, β ≠ 0. An integro-differential equation is singular if the kernel of integral transform tends to infinity at one or several points of the function domain. An example is the Prandtl equation for air circulation around the plane wing

which is also common for other fields of applied mathematics. Another example is one of the forms of heat conduction equation, which takes into account a finite speed of heat transport in the medium

where τ is the relaxation time. Analytical solutions of integro-differential equations can sometimes be achieved by reducing them to differential or integral equations and applying sufficiently worked out methods to solve the latter. In some cases, a method of separation of variables can be useful for reducing a partial integro-differential equation to an ordinary one (for instance, Eq. (2)). Semianalytical solutions of ordinary linear integro-differential equations containing an integral Volterra operator with a difference kernel can be obtained by the Laplace Transform method. Nowadays, numerical methods for solution of integro-differential equations are widely employed which are similar to those used for differential equations.