The Graetz number, Gz, is a nondimensional group applicable mainly to transient heat conduction in laminar pipe flow. It is defined as
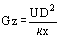
where U is the velocity of the fluid, D the diameter of the pipe, κ the fluid thermal diffusivity (λ/ρcp) and x the axial distance along the pipe.
Gz represents the ratio of the time taken by heat to diffuse radially into the fluid by conduction (sometimes called the "relaxation time"), D2/κ, to the time taken for the fluid to reach distance x, x/U, i.e.,

For small values of Gz (Gz < 20) radial temperature profiles are fully developed, but for larger values thermal boundary layer development has to be taken into account.
Note that

and Gz−1 is often used as a nondimensional form of axial distance in the representation of entrance effects on laminar flow heat transfer.
Graetz number is the reciprocal of Fourier number with time replaced by x/U, and many of the equations for transient heat conduction in laminar pipe flow are analogous to those of transient heat conduction in cylinders.
REFERENCES
Hewitt, G. F, Shires, G. L. and Bott, T. R. (1994) Process Heat Transfer, CRC Press, Boca Raton, FL, USA.
References
- Hewitt, G. F, Shires, G. L. and Bott, T. R. (1994) Process Heat Transfer, CRC Press, Boca Raton, FL, USA.