The electromagnetic flowmeter is one of the most successful nonintrusive types of flowmeter. The basic concept that an emf is induced in a conducting liquid moving through a magnetic field, in accordance with Faraday’s Law of electromagnetic induction, has been known since the early part of the last century. However, it was not until the 1950s that industrial applications became a reality. Some of the earliest applications were concerned with measuring the flow rate of blood, Kolin (1960).
The primary device consists of an electrically-insulating metering tube, typically within a nonmagnetic stainless-steel tube. The choice of liner material depends mainly on the liquid, which can range from slurries or molasses to chemically-aggressive mixtures or molten metals. Conductivity thresholds as low as 5 micro-Siemen/cm are common, with some manufacturers claiming considerably lower values. When measuring the flow rate of an electrolyte, a further problem is that because of the relatively low ion mobility, conductivity is likely to be affected by the flow, making it a function of velocity.
One or more pairs of electrodes, diametrically-opposed, are set into the wall such that the diameter on which they lie, the magnetic field and the flow direction are mutually orthogonal. If the typical electrodes, e.g., dome-headed screws, are replaced by relatively large plates, the larger measuring areas can sometimes reduce the effect of nonstandard flow patterns on the meter. Such electrodes, however, are more prone to fouling, introducing additional errors. The secondary device processes the signal from the electrodes, typically millivolts. It provides outputs which can be in volts, milliamps or pulses per second. Usually, a reference signal from the primary device—which is proportional to the magnetic flux—is compared in the secondary device with the flow signal.
The use of direct current as a means of exciting the magnet has been quickly discarded because of the difficulty of electrochemical and polarization emfs appearing at the electrodes, and for many years excitation by alternating current was the norm. However, a ‘transformer’ effect can exist since the conducting liquid, the electrodes and leads effectively form a single-turn loop, giving rise to a quadrature signal which can be of the same order of magnitude as the metering signal. It should be possible to remove the quadrature signal but complications arise when, for example, liquid conductivity is not uniform or earthing difficulties exist. Since the mid-1970s most manufacturers have used square or trapezoidal-wave excitation, operating usually at a few Hertz and minimizing most of the above difficulties. An additional benefit is that the zero is continually reestablished, avoiding the earlier problems associated with zero drift [Baker (1982)]. The impedance of the liquid path should ideally be at least two orders of magnitude less than that of the input of the secondary device. The situation has improved since the days of the voltameter thermionic valve and germanium transistor. Modern electronic components make it possible for input impedance of the secondary device to be several orders of magnitude greater than that of its predecessors. One of the most recent developments is to position the electrodes outside a dielectric liner, the system operating by capacitive coupling, with no contacts within the metering tube.
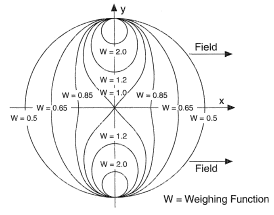
Theoretically, a uniform magnetic field can only be achieved by using an infinite magnet. This means that, for practical purposes, certain regions of the cross-section containing the electrodes will produce larger signals than others at the same velocity. Some of the earliest recorded experimental work was that by Williams (1930). He realized that since the velocity profile of a flowing liquid was rarely flat, the emf existing across the pipe diameter deriving from the central velocity would be effectively shunted by those from the slower moving flows near the pipe wall. This would give rise to circulating currents, and the measured signal would be lessened by an Ohmic drop. As it turns out, as Shercliff (1962) explains, because the induced currents flow only in the plane normal to the meter axis, the above effect is self-cancelling if the velocity distribution is axisymmetric. Shercliff (1962) has developed the very important ‘weight-function’ map, Figure 1, which assisted in the prediction of the effects of asymmetry, especially relevant in short-pattern meters. Hartmann (1937) has pointed out that a similar ‘shorting’ takes place at the ends of the necessarily finite meter, where the magnetic intensity falls to zero. This effect has been minimized by the designs of the pole pieces.
Installation requirements are given in ISO 6817 (1992) and BS 5792 Part 1 (1993) Standards. The meter should be installed in a straight pipe at a distance of at least 10 times the nominal diameter (10 DN) from any upstream disturbance and 5 DN downstream. The flow must be swirl-free and the meter should not be larger or more than 3% smaller than the connecting pipework. To prevent the formation of gas bubbles on the electrodes, these should normally be installed horizontally. In ideal conditions, such meters should be capable of measuring flow rate with an uncertainty of 0.2%.
REFERENCES
Baker, R. C. (1982) Electromagnetic flowmeters. in: Scott, R. W. W. (Ed). London and New Jersey; Applied Science Publishers Ltd.
British Standards Institution (1993) Measurement of conductive liquid flow in closed conduits - Method Using Electromagnetic Flowmeters. BS 5792, Part 1, London.
Hartmann, J. (1937) Hg-dynamics 1, Math-Fys. Medd. 15. No. 6. (Royal Danish Academy of Science and Letters).
International Organization for Standardization (1992) Measurement of conductive liquid flow in closed conduits - method using electromagnetic flowmeters. ISO 6817.
Kolin, A. (1960) Circulatory system; methods; Blood flow determination by the electromagnetic method. in: Glasser, O. (Ed). Medical Physics, 3: 141. Chicago I11: Year Book Medical Publishers.
Shercliff, J. A. (1962) The Theory of Electromagnetic Flow Measurement. Cambridge University Press.
Williams, E. J. (1930) The Induction of emfs in a moving fluid by a magnetic field and its application to an investigation of the flow of liquids. Proc. Phys. Soc., London, 42: 466.
References
- Baker, R. C. (1982) Electromagnetic flowmeters. in: Scott, R. W. W. (Ed). London and New Jersey; Applied Science Publishers Ltd.
- British Standards Institution (1993) Measurement of conductive liquid flow in closed conduits - Method Using Electromagnetic Flowmeters. BS 5792, Part 1, London.
- Hartmann, J. (1937) Hg-dynamics 1, Math-Fys. Medd. 15. No. 6. (Royal Danish Academy of Science and Letters).
- International Organization for Standardization (1992) Measurement of conductive liquid flow in closed conduits - method using electromagnetic flowmeters. ISO 6817.
- Kolin, A. (1960) Circulatory system; methods; Blood flow determination by the electromagnetic method. in: Glasser, O. (Ed). Medical Physics, 3: 141. Chicago I11: Year Book Medical Publishers.
- Shercliff, J. A. (1962) The Theory of Electromagnetic Flow Measurement. Cambridge University Press. DOI: 10.1017/S0022112063210902
- Williams, E. J. (1930) The Induction of emfs in a moving fluid by a magnetic field and its application to an investigation of the flow of liquids. Proc. Phys. Soc., London, 42: 466.