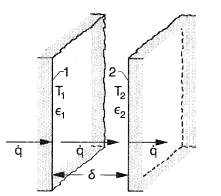
Consider two parallel plane surfaces of infinite extent that have different uniform temperatures (Figure 1). The space between the surfaces either is a vacuum or contains a material that does not interact with radiative energy; the surface properties are independent of wavelength (gray surfaces). A useful radiative exchange result is the net transfer from a unit area of surface 1 across the separation space to surface 2. This is derived in standard heat transfer texts by flux or ray tracing methods, Siegel and Howell (1992). The Emissivity (which equals the absorptivity for a gray surface) of each surface is assumed independent of the angular direction of emission. Reflected energy, however, can be diffuse, specular (mirror-like), or can have an arbitrary angular distribution, and the same result is obtained. The surface properties can depend on temperature. For these conditions, after accounting for all exchanges between the parallel boundaries, the net energy flux (W/m2) transferred by radiation from 1 to 2 is
The ε1 and ε2 are emissivities, each selected at their surface temperature. The flux  is independent of the spacing between the surfaces.
is independent of the spacing between the surfaces.
The space between the plane surfaces is now filled with a gas that does not absorb, emit, or scatter radiation, but is heat conducting. If the spacing δ is narrow, or gravity is small, free convection is suppressed. Conduction occurs and is independent of radiation so the net flux transferred is

Since the gas does not interact with radiation, convection can also be added to Equation (1a) as an independent mode of heat transfer.
If the surface properties depend on wavelength, Equation (1a) is written spectrally by using the blackbody function instead of σT4. The net radiative transfer is obtained by integrating over all wavelengths to yield
where the ε are now functions of wavelength and temperature.
A technique for reducing radiative transfer is to place a series of highly reflecting thin parallel plates (radiation shields) in an evacuated space between two boundaries. As shown in Figure 2, there are N thin plates, all with gray properties and having the same property restrictions as for Equation (1a). Each thin plate, such as the nth plate, has emissivities, εn,1 and εn,2 on its sides; for simplicity the ε are assumed independent of temperature. The net energy transfer is

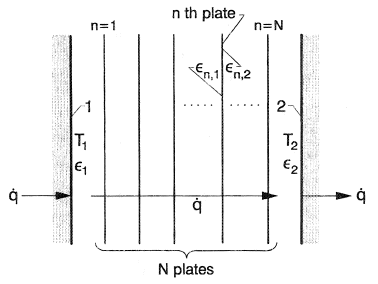
Figure 2. Radiative transfer between infinite parallel boundaries with N radiation shields between them.
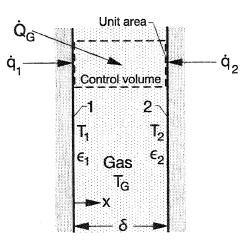
Figure 3. Infinite parallel boundaries with absorbing and emitting gas at uniform temperature TG between them.
The complexity of having an absorbing and emitting gas between the plane boundaries is now added to Equation (2). The gas is mixed, as in a furnace, so it is at uniform temperature TG (Figure 3). Energy is either being added to or removed from the gas to maintain TG at steady state in the presence of the radiative interaction with the boundaries at T1 and T2. The net radiative energy leaving surface 1 is not equal to that removed at 2 (they are equal for the conditions of Eq. (2)). A control volume is considered bounded by opposing unit areas of the boundaries and extending across the space δ (Figure 3). The  ,
,  , and
, and  are the energy quantities that must be supplied, by some means other than internal radiation, to the control volume boundaries on surfaces 1 and 2, and to the gas in the control volume, to maintain their steady temperatures. If any of these energies are negative, then energy is being removed from the corresponding surface (such as by external cooling of the boundary) or gas. From an overall energy balance,
are the energy quantities that must be supplied, by some means other than internal radiation, to the control volume boundaries on surfaces 1 and 2, and to the gas in the control volume, to maintain their steady temperatures. If any of these energies are negative, then energy is being removed from the corresponding surface (such as by external cooling of the boundary) or gas. From an overall energy balance,  , so the energy added to the gas, for example by combustion, is
, so the energy added to the gas, for example by combustion, is  . Because of energy absorption in the gas, the directional behavior of radiation leaving a surface is significant since it determines the path length through the gas; for Equations (4a) and (4b) both the reflected and emitted energies from the boundaries are diffuse. The energy fluxes supplied externally to surfaces 1 and 2 to compensate for their net radiative losses are
. Because of energy absorption in the gas, the directional behavior of radiation leaving a surface is significant since it determines the path length through the gas; for Equations (4a) and (4b) both the reflected and emitted energies from the boundaries are diffuse. The energy fluxes supplied externally to surfaces 1 and 2 to compensate for their net radiative losses are
The mean spectral transmittance accounting for all directions of diffuse radiation through the gas is  , where E3 is the exponential integral function (tabulated in Siegel and Howell (1992) and in handbooks),
, where E3 is the exponential integral function (tabulated in Siegel and Howell (1992) and in handbooks),
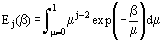
with j = 3. The radiative behavior depends on the spacing δ between boundaries; Equations (1a) and (2) are independent of spacing.
A special case is for a gray gas (aλ = a) between diffuse-gray parallel boundaries. Equations (4a) and (4b) then become
For a nonabsorbing (transparent) medium between the boundaries  , and Equations (5a) and (5b) each become the same as Equation (1a) (there is a negative sign for
, and Equations (5a) and (5b) each become the same as Equation (1a) (there is a negative sign for  as its direction is opposite to
as its direction is opposite to  ). For a highly absorbing medium
). For a highly absorbing medium  , which results in
, which results in
Since for a gray boundary ε = α, Equations (6a) and (6b) are each a local balance stating that the energy flux that must be supplied externally to a boundary to maintain its specified temperature is equal to its emission at its surface temperature minus absorption of energy emitted to it by the gas.
Now consider an absorbing and emitting stationary gas between parallel black surfaces with heat conduction in the gas. The gas attains a temperature distribution that depends on the local balance within it of radiant absorption, emission, and heat conduction. The energy balance in dimensionless form, Equation (7a), equates the gain by conduction to the loss by local radiant emission reduced by the radiant energy gained as a result of emission from the black boundaries and the other volume elements of the gas,
Equation (7a) is an Integrodifferential Equation for the temperature distribution t(κ); the solution depends on κδ, t2, and N1. The boundary conditions are t(0) = 1 and t(κδ) = T2/T1 = t2. The net transfer from boundary 1 to 2 by conduction and radiation is
Numerical solutions, Viskanta and Grosh (1962), give results for  as in Table 1.
as in Table 1.
Table 1. Heat transfer between parallel black surfaces by combined radiation and conduction through a gray medium

If the gas between the boundaries is a good absorber, the heat transfer can be obtained accurately by using a diffusion approximation. Radiation is represented as an effective heat conduction where, for a gray gas, the effective radiative conductivity depends on the local gas temperature to the third power. The energy equation is

and the heat transfer by combined radiation and conduction is obtained from

The solution for a gray medium between plane boundaries is in Siegel and Howell (1992), and a spectral analysis is in Siegel and Spuckler (1994).
Nomenclature
a absorption coefficient, 1/m
aλ spectral absorption coefficient, 1/m
Ej exponential integral function of order j
eλb spectral blackbody function, W/m3
N number of thin plates
N1 conduction-radiation parameter 
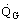 rate of energy addition to gas in control volume, W
rate of energy addition to gas in control volume, W
 heat flux, W/m2
heat flux, W/m2
T absolute temperature, K
t dimensionless temperature T/T1
x coordinate between surfaces (origin at surface 1), m
α absorptivity of surface
δ spacing between parallel surfaces, m
ε emissivity of surface
κ optical coordinate ax; κδ, optical thickness aδ
λ wavelength, m; thermal conductivity, W/m·K
σ Stefan-Boilzmann constant, W/m2·K4
 mean transmittance
mean transmittance
Subscripts
G gas
n the nth radiation shield
1,2 the two parallel surfaces
λ spectral quantity
REFERENCES
Siegel, R. and Howell, J. R. (1992) Thermal Radiation Heat Transfer, 3rd edn., Hemisphere Publishing Corporation, Washington DC.
Siegel, R. and Spuckler, C. M. (1994) Approximate solution methods for spectral radiative transfer in high refractive index layers, Int. J. of Heat and Mass Trans., 37 (Suppl. 1), 403-413. DOI: 10.1016/0017-9310(94)90040-X
Viskanta, R. and Grosh, R. J. (1962) Effect of surface emissivity on heat transfer by simultaneous conduction and radiation, Int. J. of Heat and Mass Trans., 5, 729-734. DOI: 10.1016/0017-9310(62)90203-X
References
- Siegel, R. and Howell, J. R. (1992) Thermal Radiation Heat Transfer, 3rd edn., Hemisphere Publishing Corporation, Washington DC.
- Siegel, R. and Spuckler, C. M. (1994) Approximate solution methods for spectral radiative transfer in high refractive index layers, Int. J. of Heat and Mass Trans., 37 (Suppl. 1), 403-413. DOI: 10.1016/0017-9310(94)90040-X
- Viskanta, R. and Grosh, R. J. (1962) Effect of surface emissivity on heat transfer by simultaneous conduction and radiation, Int. J. of Heat and Mass Trans., 5, 729-734. DOI: 10.1016/0017-9310(62)90203-X