Many factors are involved in determining the vapor-to-condenser surface heat transfer coefficient during condensation. The problem is even more complex when the vapor contains different molecular species which may or may not condense (see Condensation of Multicomponent Vapors). The term “pure vapor” implies that only one species is present.
In industrial Condensers, vapor and condensate flows are, in general, three-dimensional and involve effects of gravity, shear stress at the condensate surface due to vapor velocity, interface temperature difference due to nonequilibrium and inundation, i.e., condensate from higher or upstream surfaces impinging on lower or downstream surfaces. For profiled surfaces (e.g., finned tubes), surface tension effects are also important. Condensate and vapor flows may be either laminar or turbulent. The condensate may form a continuous film on the surface or, when the surface is not wetted by the condensate, form discrete droplets (see Dropwise Condensation). Condensation may occur on external surfaces, e.g., on the outside of the tubes in a shell-and-tube condenser or on internal surfaces, e.g., in-tube condensation. (See Tubes, Condensation on Outside in Cross Flow; Tube Banks, Condensation Heat-Transfer in; Tubes, condensation in.) In “direct contact” condensation, liquid at a temperature below the saturation temperature is brought into contact with the vapor. The extent to which the condensation process is understood and the accuracy with which heat transfer coefficients can be calculated depend on the circumstances. After almost a hundred years of research, accurate predictions can now be made for relatively simple geometry (e.g., flat-plate or single horizontal tube) and for well-defined flow conditions.
The fact that, during condensation, equilibrium conditions cannot prevail at the vapor-condensate interface, means that a temperature difference must occur in the vicinity of the interface. Extrapolations to the interface of the temperature distributions in the vapor and liquid would indicate a discontinuity, the “interface temperature drop.” As discussed by Niknejad and Rose (1981), the problem has been studied for many years and it is now established that the interface temperature drop is essentially confined to a region in the vapor having a thickness of a few mean free paths of the vapor molecules. Various related theoretical approaches lead to the expression
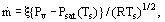
where  is the net condensation mass flux, Pv is the vapor pressure, Psat(Ts) is the saturation pressure at the liquid surface temperature, Ts and R is the specific gas constant of the vapor. ξ is a dimensionless quantity of order unity, and can be considered as an interface mass transfer coefficient. Experiment and theory show that ξ depends on
is the net condensation mass flux, Pv is the vapor pressure, Psat(Ts) is the saturation pressure at the liquid surface temperature, Ts and R is the specific gas constant of the vapor. ξ is a dimensionless quantity of order unity, and can be considered as an interface mass transfer coefficient. Experiment and theory show that ξ depends on  , ξ increasing with increasing
, ξ increasing with increasing , the dependence being most marked at low pressure. However, as tends to zero (equilibrium), ξ approaches a constant value which is independent of pressure and condensing fluid.
, the dependence being most marked at low pressure. However, as tends to zero (equilibrium), ξ approaches a constant value which is independent of pressure and condensing fluid.
A difficulty which arises in the theory of interphase matter transfer is that it is not certain that all vapor molecules striking the liquid surface remain in the liquid phase, i.e., some molecules may be reflected. Some theoretical models incorporate the parameter σ, the “condensation coefficient” defined as the fraction of those vapor molecules impinging on the liquid surface which remain in the liquid phase, σ being assumed to have a constant value. In these models, ξ0 (the value of ξ in Eq. (1) for 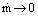 ) is a function of σ. Other approaches assume that no vapor molecules are reflected at the liquid surface when = 1 and is a constant. Various theoretical models lead, with σ= 1, to values of ξ0 between about 0.6 and about 0.8. While earlier experimental investigations gave much lower values—which were interpreted as indicating low values of σ (down to around 0.01)— more recent studies indicate a value near 0.7, confirming the validity of the theory and suggesting that σ is equal to or near unity. The most probable explanation of the earlier low values is the presence in the vapor of noncondensing gas, leading to a significant temperature drop in the vapor which was erroneously attributed to the interface.
) is a function of σ. Other approaches assume that no vapor molecules are reflected at the liquid surface when = 1 and is a constant. Various theoretical models lead, with σ= 1, to values of ξ0 between about 0.6 and about 0.8. While earlier experimental investigations gave much lower values—which were interpreted as indicating low values of σ (down to around 0.01)— more recent studies indicate a value near 0.7, confirming the validity of the theory and suggesting that σ is equal to or near unity. The most probable explanation of the earlier low values is the presence in the vapor of noncondensing gas, leading to a significant temperature drop in the vapor which was erroneously attributed to the interface.
For a saturated vapor and for moderate departure from equilibrium at the interface when the vapor temperature Tν≈Ts, Eq. (1) with the Clapeyron-Clausius Equation, leads to the following expression for the interface heat transfer coefficient αi:

where hlg is the specific latent heat of evaporation, vg is the specific volume of saturated vapor, vl is the specific volume of saturated liquid and vlg=vg-vl, and R is the specific ideal-gas constant. When the vapor is treated as an ideal gas and with vg>>vl, Eq. (2) gives:

With ξ0 = 0.7, Eq. (3) gives values of αi much higher than the heat transfer coefficient for the condensate in film condensation, except in the case of liquid metals. For example, for steam at 30°C, αi≈1.1 MW/m2 K, which may be compared with typical values of the heat transfer coefficient in the range 10–50 kW/m2 K for the condensate film during film condensation. The interface resistance is therefore, apart from the case of liquid metals, generally negligible for practical purposes.
The problem of laminar film condensation was first treated by Nusselt (1916) for condensation on a vertical plane surface and on a horizontal tube: For a saturated vapor with uniform condenser wall temperature and assuming that the motion of the condensate is controlled solely by gravity and viscosity; that acceleration of the condensate film is negligible; that shear stress on the condensate surface due to the vapor is negligible; that heat transfer across the condensate film is by pure conduction; and that the condensate properties do not vary across the film, the following expressions for local film thickness and for the local and average heat transfer coefficient and Nusselt number are obtained:
For a vertical plane surface:
local condensate thickness
(4)
local heat transfer coefficient
(5)
mean heat transfer coefficient
(6)
mean Nusselt number
(7)
where η is liquid viscosity; λ is the liquid thermal conductivity; ρ, the liquid density; Δρ is the difference between liquid and vapor density; ΔT is the vapor-to-condensing surface temperature difference; x is the distance from top of vertical plate; L is the plate height and g is the specific force of gravity.
For a horizontal tube:
local condensate thickness
(8)
where

and θ is the angle measured from the top of the tube,
local heat transfer coefficient
(10)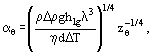
mean heat transfer coefficient
(11)
mean Nusselt number.
(12)
where d is the tube diameter.
In the treatment of horizontal tube, the additional approximation that the condensate film thickness is much less than the tube radius is required. Since Eq. (9) indicates that δθ→∞ for θ→π, this approximation is evidently invalid near the bottom of the tube. However, as the film becomes thicker, the local heat flux becomes small and the contribution of the erroneous values near the bottom of the tube are insignificant in the calculation of the total heat transfer rate or mean heat flux for the tube. For quiescent vapor, Eqs. (6), (7), (11) and (12) have been very well verified by experiment.
The advent of the computer has made possible more complete solutions to the problem of laminar film condensation. These have shown that the Nusselt assumptions lead to very accurate results for the practical range of operating conditions. A generally small correction has been proposed—i.e., that hlg in Eqs. (4–7) should be replaced by hlg+(3/8)cpΔT and in Eqs. (8–12), by hlg+0.68cpΔT, where cp is the isobaric specific heat capacity of the condensate. A satisfactory reference temperature for the evaluation of properties of condensate film is:

where Tv is the temperature of the bulk vapor and Tw that of the condensing surface, and hlg is evaluated at Tv.
The Nusselt assumptions have been used for the case where the surface heat flux, rather than surface temperature, is uniform. This leads, for the vertical plate, to the same expressions as Eqs. (6) and (7), with the uniform heat flux and mean temperature difference replacing the mean heat flux and uniform temperature difference. For the horizontal tube case, the coefficient in Eqs. (11) and (12) becomes 0.695. However, as indicated by Rose (1988), the validity of the solution is questionable since the mean value of the temperature difference is significantly affected by the erroneously large values near the bottom of the tube where the condensate film becomes thick. In practice, the surface temperature variation around a horizontal condenser tube approximates to a cosine distribution. It is interesting to note that in this case, the coefficient in Eqs. (11) and (12) (with mean heat flux and mean surface temperature) is negligibly affected [see Memory and Rose (1991)].
When the vapor velocity over the condensing surface is significant, account must be taken of the shear stress at the condensate surface. This problem is discussed and reviewed in some detail by Rose (1988).
For the case of condensation with vapor flow along a horizontal plane surface, the surface shear stress, τδ, is given by
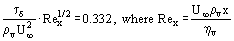
for very low condensation rates, and by

for high condensation rates, where U∞ is the free stream velocity of the vapor, ρν is the vapor density and ην, the vapor viscosity and x is distance from the leading edge. In the general case, the problem requires simultaneous solution of the conservation equations for the vapor and condensate with appropriate conditions at the interface [see Rose (1988)]. When the Nusselt assumptions are used for the condensate film, Eq. (14) leads to

where

and Eq. (15) gives

Equations (16) and (18) are both conservative, i.e., they underestimate the heat transfer coefficient; Equation (16) is more accurate when G < about 1 and Eq. (18) is more accurate when G > about 1. Solutions have also been obtained for vapor downflow on a vertical plate. The results are summarized by the interpolation formula:

where

and  .
.
For condensation on a horizontal tube, the problem is complicated by separation of the vapor boundary layer. An approximate solution, given by Shekriladze and Gomelauri (1966), uses the high condensation rate limiting value of the surface shear stress [analogous to Eq. (15) for the flat plate]. This underestimates the surface shear stress, and hence the heat transfer coefficient, and should lead to conservative results. The mean heat transfer coefficient for vertical vapor downflow on a horizontal tube, using this approach, is given to within 0.4% by the equation

where  .
.
Equation (21) is in fair agreement with experimental data for various fluids. A more detailed discussion of this problem is given in Tubes, Condensation on the Outside in Crossflow.
An additional factor affecting the performance of multitube condensers is inundation, i.e., condensate from higher or upstream tubes falling under gravity or being carried by the vapor flow onto lower or downstream tubes. For the case of negligible vapor velocity, Nusselt has extended his analysis by assuming that condensate drains from a tube as a continuous sheet onto the tube below and obtained, for the mean heat transfer coefficient for a column of n tubes,

where α1 is the heat transfer coefficient for the top tube. Experimental data are very scattered but indicate that Eq. (22) is very conservative. An index of –1/6 is frequently used in design, but this is probably also conservative.
Turbulent film condensation is much less well-understood than the laminar case, particularly in the presence of significant vapor shear stress. Transition from laminar to turbulent film condensation occurs at a film Reynolds number (4Γ/η) between 1 000 and 2 000. is the condensate mass flow rate per width of surface. Various theoretical models have been proposed which treat the turbulence and the effect of surface shear stress in somewhat different ways. Experimental data are generally for condensation inside tubes. In circumstances where the condensate forms a thin film on the tube wall (stratified flow), and particularly for the case of a vertical tube with vapor downflow, the data are suitable for validation of turbulent condensation models. Experiment and theory both indicate that the heat transfer coefficients for turbulent film condensation are appreciably higher than for the laminar case. Various models and calculation methods are described by Butterworth (1983), Marto (1991) and Stephan (1992).
Except in the case of steam and liquid metals, for condensation on the outside surface of tube, the vapor-side resistance is usually controlling owing to the low thermal conductivity of the condensate. For a water-cooled condenser tube, the coolant-side heat transfer coefficient might typically be around 5 000 W/m2K. This is of similar magnitude to that found with film condensation of steam (5 000–15 000 W/m2K). For organic vapors, condensing-side heat transfer coefficients are lower typically by a factor of 5 or more. There is therefore considerable incentive to enhance the condensing-side heat transfer, particularly for organic vapors such as refrigerants.
A commonly-used enhancement method, particularly in refrigeration and air-conditioning plant, is the use of horizontal low-finned tubes. Here, the tube diameter is typically around 20 mm while the height of the radial integral fins is normally around 1 mm. Increase in the condensing-side heat transfer coefficient by factors of 7 or more is achieved for fluids with low surface tension. The enhancement arises from the increase in surface area, the low effective height of the fins [see Eq. (6)] and surface tension-enhanced condensate drainage due to the streamwise pressure gradient set up in the film by surface curvature changes. Surface tension also has a detrimental effect due to capillary retention of condensate between fins on the lower part of the surface. For this reason enhancement factors for condensation of steam are lower (typically 2 to 3) owing to the high surface tension of water. (See also Augmentation of Heat Transfer, Two-Phase Systems.)
To date, techniques for promoting dropwise condensation have only been successful on the laboratory scale for fluids with high surface tension, notably steam. The fact that heat transfer coefficients for dropwise condensation of steam are 10 to 20 times those for film condensation continues to stimulate research in this field. More information on dropwise condensation is given in the article (Dropwise Condensation).
Direct contact condensation, where vapor and liquid are brought into contact without an intervening wall, is sometimes used for special applications. Liquid may be sprayed into an atmosphere of vapor or vapor may be injected into a pool of liquid. In both cases, the limiting heat transfer mechanism is conduction in the liquid. Direct contact condensation has been discussed by Jacobs (1985).
REFERENCES
Butterworth, D. (1983) Film Condensation of a Pure Vapour. Heat Exchanger Design Handbook, Ed. E. U. Schlunder, Hemisphere, New York, 1989.
Jacobs, H. R. (1985) Direct Contact Condensers. Heat Exchanger Design Handbook, Ed. E. U. Schlunder, Hemisphere, New York, 1989.
Marto, P. (1991) Heat Transfer in Condensation, in Boilers, Evaporators and Condensers. Ed. S. Kakac, Wiley, 525-570.
Memory, S. B. and Rose, J. W. (1991) Free Convection Laminar Film Condensation on a Horizontal Tube with Variable Wall Temperature. Int. J. Heat Mass Transfer. 34, 2775-2778. DOI: 10.1016/0017-9310(91)90236-8
Niknejad, J. and Rose, J. W. (1981) Interphase Matter Transfer—an Experimental Study of Condensation of Mercury. Proc. R. Soc. Lond. A 378, 305-327.
Nusselt, W. (1916) Die Oberflachenkondensation des Wasserdampfes. Z Vereines Deutch. Ing. 60, 541-546, 569-575.
Rose, J. W. (1988) Fundamentals of Condensation Heat Transfer: Laminar Film Condensation. JSME Int. Journal, Series II, 31 (3), 357-375.
Shekriladze, I. G. and Gomelauri, V. I. (1966) Theoretical Study of Laminar Film Condensation of Flowing Vapour. Int. J. Heat Mass Transfer, 9, 581-591. DOI: 10.1016/0017-9310(66)90092-5
Stephan, K. (1992) Heat Transfer in Condensation and Boiling. Springer-Verlag.
References
- Butterworth, D. (1983) Film Condensation of a Pure Vapour. Heat Exchanger Design Handbook, Ed. E. U. Schlunder, Hemisphere, New York, 1989.
- Jacobs, H. R. (1985) Direct Contact Condensers. Heat Exchanger Design Handbook, Ed. E. U. Schlunder, Hemisphere, New York, 1989.
- Marto, P. (1991) Heat Transfer in Condensation, in Boilers, Evaporators and Condensers. Ed. S. Kakac, Wiley, 525-570.
- Memory, S. B. and Rose, J. W. (1991) Free Convection Laminar Film Condensation on a Horizontal Tube with Variable Wall Temperature. Int. J. Heat Mass Transfer. 34, 2775-2778. DOI: 10.1016/0017-9310(91)90236-8
- Niknejad, J. and Rose, J. W. (1981) Interphase Matter Transfer—an Experimental Study of Condensation of Mercury. Proc. R. Soc. Lond. A 378, 305-327. DOI: 10.1098/rspa.1981.0154
- Nusselt, W. (1916) Die Oberflachenkondensation des Wasserdampfes. Z Vereines Deutch. Ing. 60, 541-546, 569-575.
- Rose, J. W. (1988) Fundamentals of Condensation Heat Transfer: Laminar Film Condensation. JSME Int. Journal, Series II, 31 (3), 357-375.
- Shekriladze, I. G. and Gomelauri, V. I. (1966) Theoretical Study of Laminar Film Condensation of Flowing Vapour. Int. J. Heat Mass Transfer, 9, 581-591. DOI: 10.1016/0017-9310(66)90092-5
- Stephan, K. (1992) Heat Transfer in Condensation and Boiling. Springer-Verlag. DOI: 10.1002/cite.330650508