Boiling is the process of turning a liquid at its saturation temperature into vapor by applying heat. A similar process occurs when the pressure applied to a hot liquid is reduced: this would normally be called flashing. Production of cavities in a cold liquid by the application of negative pressures (tensions) is called cavitation.
In the popular imagination, boiling is associated with the rapid formation of vapor bubbles in a rather chaotic manner. This is normally correct, though boiling can also occur by evaporation at large liquid–vapor interfaces without the appearance of vapor bubbles: in particular, in high velocity annular flows where there is only a thin liquid film on the heated surface. In both cases, there is liquid in contact with the surface and the heat transfer is good. When the temperature of the heated surface is very high, the characteristics of the boiling process change. It is no longer possible for the liquid to come into good contact with the surface. There is a film of vapor separating solid and liquid, preventing good heat transfer. If there is plenty of liquid present, this vapor film may be quite smooth and orderly.
Boiling is a widespread phenomenon in industry. The reasons for using the process vary. In a power station using steam turbines, the vapor itself is the desired product (for a description of boilers as equipment see Boilers). When cooling electronic components, it is the good heat transfer characteristics of boiling that are important. On the other hand, in the analysis of hypothetical loss of coolant accidents in water-cooled nuclear power stations, it is the rather poorer heat transfer that can occur at high surface temperatures that is of interest.
It is usual to base more detailed discussion of the types of boiling on a boiling curve such as that shown in Figure 1. The boiling curve is a graph of heat flux  versus wall superheat ΔTSAT, the difference between the wall temperature and the saturation temperature (or boiling point). The curve is often drawn with log scales to accommodate the rather large range of variables. The general shape of the curve remains much the same for a variety of boiling situations. The actual values of
versus wall superheat ΔTSAT, the difference between the wall temperature and the saturation temperature (or boiling point). The curve is often drawn with log scales to accommodate the rather large range of variables. The general shape of the curve remains much the same for a variety of boiling situations. The actual values of  and ΔTSAT will depend on other details, in particular, what fluid is being boiled and what the flow rate is. For the moment, Pool Boiling is assumed, i.e., there is no pump causing large-scale convection of the liquid.
and ΔTSAT will depend on other details, in particular, what fluid is being boiled and what the flow rate is. For the moment, Pool Boiling is assumed, i.e., there is no pump causing large-scale convection of the liquid.
![Boiling curve for a heated, 0.14 mm diameter, platinum wire in water at atmospheric pressure [(Nukiyama (1934)].](/content/5012/90BFig1.gif)
Figure 1. Boiling curve for a heated, 0.14 mm diameter, platinum wire in water at atmospheric pressure [(Nukiyama (1934)].
Before discussing the boiling curve in any detail, two observations must be made. Firstly, it is not easy to do an experiment to get results resembling Figure 1; if one attempts a simple experiment with an electrical heater immersed in a pool of liquid and varies the power supplied to the heater, one might obtain a curve that looks markedly different. Nukiyama did not obtain any results in the region of negative slope in Figure 1, but he argued that such a region must exist. Prior to his work, there was disagreement as to whether there was a maximum on the curve — very high heater powers are needed to reach it. The second observation is that, for many practical purposes, the entire curve to the right of Point e in the figure can be ignored. The reason for this is that the designer is normally interested in good heat transfer, i.e., high heat removal rates at low temperature differences. This can be achieved using the portion of the curve to the left of Point e.
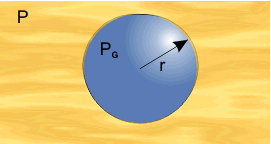
Consider now the boiling curve in more detail. Starting on the left at a low temperature difference, in the region a–b, there is no boiling taking place; heat transfer is by convection. It might seem odd that there is no boiling when the wall superheat ΔTSAT is positive, i.e., the temperature of the wall and of the liquid in contact with the wall are both above the saturation temperature. However, it turns out that there is a problem of nucleating the phase change, connected with the existence of surface tension. Suppose that somehow a small spherical vapor bubble had appeared in the liquid.
It is a standard result that mechanical equilibrium of the vapor bubble requires:

where pG is the vapor pressure, p the external pressure, s the surface tension, and r the radius of the bubble. But the definition of saturation temperature is that pG = p (i.e., the requirement for thermal equilibrium is pG = p). Even with pG slightly greater than p, the vapor region cannot grow. In the initial stages of bubble formation r will be small and the 2σ/r term very large.
In practice, two conditions have to be met for nucleation. Firstly, pG must be greater than p, and secondly, a pre-existing vapor region is needed to provide a nucleation site, such that Eq. (1) can be satisfied. It is generally considered that these nucleation sites are cavities or cracks in the solid surface which have not been completely filled with liquid. They are too small to be seen by the naked eye and anyway, in boiling, things happen too quickly to be easy to follow. (However, the process of dissolved gas coming out of solution is in principle similar, but occurs more slowly. The stream of bubbles of gas, that seem to all come from the same point on the inside of a glass of beer or lemonade, have been nucleated at a surface cavity.)
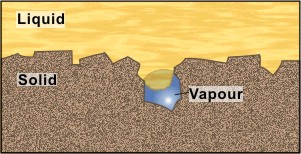
The reason that some surface cavities always contain a vapor embryo is also connected with surface tension. The analogy between the two cases in Figure 3 is not particularly close. The window sill design is clearly strongly influenced by gravity — one would not install it upside down. Active surface cavities have dimensions of around 1 μm; gravity is now unimportant compared with surface tension. Surface tension will oppose liquid entry, in the intervals between bubble nucleation, provided the curvature of the meniscus is as shown, i.e., concave on the liquid side. For further information the article on Nucleation should be consulted.
|  |
| (a) |
|  |
| (b) |
Figure 3. a) Macroscopic. The cavity prevents rain running under the windowsill. b) Microscopic. Surface tension opposes liquid entering cavity.
Returning to the boiling curve, e.g., Figure 4, the significance of Point b can now be understood. The liquid superheat, ΔTSAT is high enough to initiate boiling at the first surface cavities, i.e., the ones with the largest radius r. As the temperature or power are raised further, the number of active sites increases until at Point c boiling is in evidence all over the surface. The region c–d is called the nucleate boiling region. Initially, the role of the individual nucleation sites is fairly clear. At higher power levels, the rate of generation of vapor bubbles is such that they coalesce to form vapor columns streaming away from the surface. Nucleate boiling is the type of boiling familiar in the kitchen; for example, on the element of an electric kettle.

Figure 4. Pool boiling of water on a horizontal plate at 1 atm. (data points from Abbassi et al. 1989).
By Point d (Figure 4), the rate of vapor generation is such that it is starting to impede the flow of fresh liquid onto the surface. At Point e a crisis is reached. In pool boiling, this crisis is interpreted as a maximum possible flow rate in the counterflow of vapor away from the surface and liquid towards the surface. This is the critical heat flux. If the power to the heater is increased further then, in the steady-state, the only point on the boiling curve corresponding to this higher power level is at g and the wall temperature will jump to a much higher value. In pool boiling, and with normal heater construction, this jump in temperature may well be several hundred degrees and sufficient to destroy the heater. For this reason, the critical heat flux is often referred to as Burnout. Alternative names are departure from nucleate boiling, DNB and dryout. An ability to predict the critical heat flux is clearly very important.
Rather than considering region e–f, it seems appropriate to consider region f–g next. As already mentioned, the full curve of Figure 4 is not easy to obtain experimentally and in a power (i.e., heat flux) controlled experiment, an increase in heat flux above the critical value lead to Point g. This is in the film boiling region. The heated surface is now covered with a film of vapor, which impedes the heat transfer. Once film boiling is established, the entire film boiling region can be covered by increasing or reducing the power supplied to the heater. Point f is known as the minimum film boiling point.
The region e–f is known as transition boiling (sometimes called unstable film boiling). It has the very unusual characteristic of a negative slope, i.e., as the driving temperature difference increases, the heat transfer rate worsens, contrary to all experience of single-phase heat transfer. The physical explanation is that as the surface temperature increases, the situation changes rapidly from near-complete liquid contact with the surface in nucleate boiling to near-complete vapor contact in film boiling. Liquid contact leads to good heat transfer and vapor contact to poor heat transfer. Measurements of the extent of liquid–solid contact have been made by, amongst others, Alem Rajabi et al. (1988). They have found, in pool boiling of methanol, that the degree of liquid-solid contact decreases rapidly from 65% at the critical heat flux to less than 1% at minimum film boiling point.
The instability of transition boiling in a heat flux-controlled experiment follows directly from the negative slope. The system cannot recover from small, random, excursions in temperature. Suppose that a fluctuation caused the surface temperature to increase slightly. The heat flux removed by the boiling process reduces. Since the heat supplied continues at the same level, there is a net input of heat to the surface and the surface temperature rises, i.e., the initial small fluctuation is reinforced. The process continues until the point on the film boiling curve corresponding to the given heat flux is reached. Equally, a small negative fluctuation in temperature would have taken the boiling process all the way to the nucleate boiling curve.
How then can be transition boiling part of the curve be studied? Either by controlling the temperature of the surface instead of the heat flux, or by doing transient experiments. If the temperature is controlled — either by using a fluid at a given temperature as the heat source or by using an electrical heater with a temperature controller — then any temperature can be set and the boiling curve is single-valued — there is only one heat flux corresponding to any set temperature. Alternatively, in a transient experiment, the thermal capacity of the heater means that there cannot be instantaneous jumps in the wall temperature. All wall temperatures and all points of the boiling curve must be passed through during the transient. Transient cooling assumes some importance in quenching, when a hot solid object is immersed in a bath of cold liquid, and in the related phenomenon of Rewetting, i.e., the point during cooling when transition boiling is reached, liquid starts to contact the surface again, and heat transfer starts to improve.
Mention has already been made of the difference between a surface with a constant heat flux and one with a constant temperature. It is worth stressing the difference this makes when considering the critical heat flux. With the constant heat flux boundary condition, arising, for example, from electrical heating or from nuclear fission in a fuel rod in a nuclear reactor, exceeding the critical heat flux will lead to a large and possibly dangerous increase in temperature, i.e., the possibility of burnout. Consider now the steam generator in a sodium-cooled fast nuclear reactor (where the boundary condition on the boiler tube wall approximates the constant temperature case). The steam generator is supplied with liquid sodium at, say, 500°C. This temperature might be sufficient to place the operating point on the appropriate boiling curve for water slightly to the right of Point e; in other words, the temperature corresponding to the critical heat flux has been exceeded. Operation in this mode, in transition boiling, might be considered perfectly acceptable. There is no possibility of the wall temperature exceeding that of the heat source, 500°C. (The above examples relate to flow boiling but the principle is unchanged.)
The main features of the pool boiling curve are now considered in a more quantitative way. Large numbers of correlations and prediction methods have been suggested over the years. Here, just a few simple equations are given. In the case of nucleate boiling, all the heat transfer mechanisms increase in effect as the number of bubbles increases, i.e., as the number of active nucleation sites increases. This leads to important practical problem in predicting the heat transfer, since predicting the number of nucleating cavities is difficult. One approach is to experimentally determine a surface constant appropriate to different heater materials. Another is to relate this effect to surface roughness. In particular, because of the steepness of the nucleate boiling curve, any prediction of heat flux based on known temperatures is liable to show large errors.
Many studies of nucleate pool boiling are consistent with the heat flux 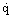 being proportional to ΔT3SAT, although in individual measurements the exponent can vary considerably from 3. Cooper (1984) analyzed data from over a hundred experiments and concluded that the accuracy of the data was insufficient to justify the complexity of many of the equations that had previously been proposed for predicting the heat transfer. Arguing that the physical properties of the boiling liquid that appear in the earlier correlations are themselves functions of parameters like the molecular weight M and the reduced pressure pr, he succeeded in producing a correlation that does not require values of surface tension, enthalpy, density, etc., as follows:
being proportional to ΔT3SAT, although in individual measurements the exponent can vary considerably from 3. Cooper (1984) analyzed data from over a hundred experiments and concluded that the accuracy of the data was insufficient to justify the complexity of many of the equations that had previously been proposed for predicting the heat transfer. Arguing that the physical properties of the boiling liquid that appear in the earlier correlations are themselves functions of parameters like the molecular weight M and the reduced pressure pr, he succeeded in producing a correlation that does not require values of surface tension, enthalpy, density, etc., as follows:

where R is the roughness in μm. Rearranging the equation, with regard to the dependence of 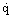 on ΔTSAT, gives
on ΔTSAT, gives 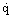 = αΔTSAT or
= αΔTSAT or 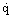 proportional to
proportional to  or
or 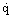 varying as
varying as 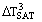 . If the roughness of the surface is unknown, one could assume R = 1 μm, i.e., log R = 0.
. If the roughness of the surface is unknown, one could assume R = 1 μm, i.e., log R = 0.
Commercial heat transfer surfaces exist on which the number of nucleation sites has been increased, e.g., by the deposition of a thin porous coating. These give better heat transfer. A fuller discussion of this topic is given in the article on Nucleate Boiling.
Often more important than the level of nucleate boiling heat transfer is the value of the critical (or burnout) heat flux. Zuber (1958) used the idea of instability in the counterflow of liquid and vapor to derive the following expression for the pool boiling critical heat flux on a flat plate:

For water at atmospheric pressure, this gives 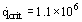 Wm–2.
Wm–2.
In general, the Zuber theory works well, although there is evidence for much lower values of 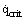 on nonwetted surfaces, e.g., for water on surfaces coated with silicon grease or PTFE [Gaertner (1965)]. Also for normal, well-wetted surfaces some authors recommend values that are 10 to 20% higher. A further discussion of the area is given in the article on Burnout (Pool Boiling).
on nonwetted surfaces, e.g., for water on surfaces coated with silicon grease or PTFE [Gaertner (1965)]. Also for normal, well-wetted surfaces some authors recommend values that are 10 to 20% higher. A further discussion of the area is given in the article on Burnout (Pool Boiling).
The next region of the boiling curve is transition boiling. Methods of predicting the heat transfer here are not well developed. A common approach is to locate the critical heat flux and minimum film boiling points and say that transition boiling follows a straight line linking the two (on a log  versus log ΔTSAT plot).
versus log ΔTSAT plot).
One method of predicting the heat flux at the minimum film boiling point was developed by Zuber (1958). Previous work had shown that the liquid-vapor interface in film boiling can become unstable, with waves appearing. These waves develop and, in practice, lead to vapor mushrooms which grow and detach from the film at regular intervals. The theory leads to a prediction for the growth rate of the vapor region. Zuber had argued that a minimum heat flux is required to evaporate this amount of liquid and provide this amount of vapor, otherwise the film would collapse. This gives a minimum film boiling heat flux of:
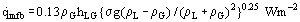
This works reasonably for a number of liquids, but measurements on hydrocarbons support Berenson’s (1960) suggestion that the constant should be 0.09.
A completely different approach is to say that at the minimum film boiling point, the liquid is at the homogeneous nucleation temperature. In general, as explained earlier, vapor cannot spontaneously nucleate in pure bulk liquid. However, as the temperature approaches the critical temperature, the distinction between liquid and vapor is becoming less pronounced (at the thermodynamic critical temperature, there is no difference between the phases). A complete and quite complex theory of homogeneous nucleation exists (see article on Nucleation). It is sufficient here to point out that one would expect the homogeneous nucleation temperature to be close to the critical temperature, Tc, and that detailed calculations give results close to:
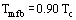
The physical argument is that once the liquid temperature reaches Tmfb, the boiling process is no longer constrained by the availability of surface cavity nucleation sites and liquid in contact with the surface will spontaneously flash into vapor, i.e., film boiling has started. There is evidence that Eq. (5) gives a reasonable estimate of the minimum film boiling point at high pressures, but Eq. (4) works better at low pressures. Of course, neither equation is enough to completely define the minimum film boiling point by itself: additional information, such as the film boiling heat transfer coefficient, is needed.
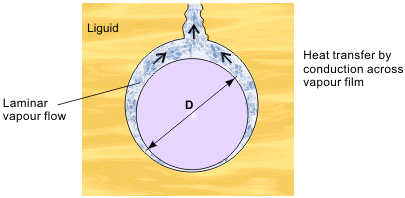
Analysis to find the film boiling heat transfer coefficient is possible, in simple geometries at least. A laminar layer of vapor builds up on the surface, with the evaporation rate at the liquid-vapor interface controlled by heat conduction and radiation through the vapor layer. The inefficiency of these processes accounts for the low heat transfer coefficients. Film boiling on a horizontal cylinder, diameter D as shown in Figure 5, has been analyzed by Bromley in 1950. The theory is the same as Nusselt’s earlier analysis for laminar film condensation on a cylinder.
The film boiling heat transfer coefficient is:

This equation assumes purely conduction heat transfer and is likely to be valid near the minimum film boiling point. At higher temperatures, the effect of radiation must be included. For a short vertical plate, of height L, D, in Eq. (6) is replaced by L and the constant becomes 0.94 instead of 0.62 (for a tall vertical plate, the film tends to break up).
A number of refinements to the theory behind Eqs. (3), (4), and (6) have been made over the years. Lienhard is particularly associated with this work, and a summary of many of the results is given in the chapter of boiling in his book (1981).
Thus far, the discussion has centered on pool boiling. Figure 6 for Forced Convective Boiling shows that in most cases, the basic shape of the boiling curve is retained. All the different regions still exist although the terminology may not be exactly the same. An improvement in heat transfer due to the forced convection is seen in all parts of the boiling curve; though it is often scarcely noticeable in nucleate boiling. A parameter that assumes a greater importance in flow boiling is the subcooling, i.e., the difference between the saturation temperature and the liquid bulk temperature. Increasing the subcooling has a similar effect to increasing the flow rate. For saturated boiling, the amount of vapor in the flow, i.e., the quality, becomes important (quality = x = vapor mass flow rate/total mass flow rate).
![Effect of mass flux (68, 136 and 203 kgm–2s–1) on the flow boiling of saturated water at 1 atm. [Cheng et al. (1978)].](/content/5012/94BFig6.gif)
Figure 6. Effect of mass flux (68, 136 and 203 kgm–2s–1) on the flow boiling of saturated water at 1 atm. [Cheng et al. (1978)].
Although it is simplest, and usual, to continue to refer to the nucleate boiling region, a better name might be the wet wall region, i.e., where the liquid is in good contact with the heat transfer surface. In subcooled boiling, and also in saturated boiling at low flow rates and qualities, bubble formation close to the wall still dominates the heat transfer, and macroscopic parameters such as subcooling and flow velocity have little effect. At higher qualities, when an annular flow pattern exists, the layer of liquid on the wall can become very thin. Also, the flow velocities are now much higher than in the single-phase liquid case (because of the presence of low density vapor). In this situation, suppression of nucleate boiling can occur. With high velocities in both vapor and liquid, the convective heat transfer in the thin liquid layer becomes very effective due to the intense turbulent mixing. Heat is transferred through the liquid layer to cause evaporation at the bulk liquid–vapor interface. This cooling process can be sufficiently effective to reduce the wall temperature below the minimum needed to activate the largest nucleation sites, i.e., nucleate boiling is suppressed, as shown in Figure 7 below.
The heat transfer mechanism when nucleate boiling is fully suppressed is called forced convection vaporization. The existence of two very different mechanisms of heat transfer makes prediction a little involved. The most successful approach appears to be the superposition approach, i.e., contributions from the two mechanisms are combined. An early correlation of the type has been published by Chen in 1966. Although this division into two mechanisms — nucleate boiling and forced convection vaporization — is widely accepted, it must be recognized that in the vast majority of cases where heat transfer measurements have been made there have been no visual observations of the boiling process.
The equations required for some of these predictions methods are quite lengthy. In addition, there is often the need for a wide range of fluid property values. A simpler method, in reasonable agreement with a large amount of data, has been suggested by Liu at al. in 1991. The two-phase heat transfer coefficient is given by:

The nucleate boiling term, αpool, is given by Eq. (2) with R = 1. The forced convection term is given by the Dittus–Boelter equation:

based entirely on liquid properties and with the total mass flow considered to be flowing as liquid, S and F, the empirical suppression and enhancements factors, as given by:

The correlation is valid for saturated boiling in vertical tubes and also horizontal tubes if the Froude Number is over 0.05. Simple extensions to lower flow rates in horizontal tubes, to flow in annuli and to subcooled boiling are explained in the original paper. A further discussion of heat transfer in the region is given in the article Forced Convection Boiling.
Prediction of the burnout point is covered in a separate article [Burnout (Forced Convection)]. Again, it may be sufficient in many cases to know the value of the critical or burnout heat flux, ensure that there is no danger of exceeding it, and then the higher temperature part of the boiling curve can be ignored. The negative slope portion of the curve is again called transition boiling.
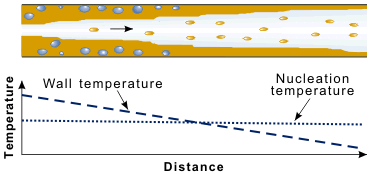
The last part of the boiling curve is normally called the post-dryout or Post Burnout region. Certainly, the term film boiling is no longer universally appropriate. The heat transfer situation may not be that of a thin vapor film between the heat transfer surface and bulk liquid; indeed, there may well not be any continuous bulk liquid present, only liquid drops. This situation is shown in Figure 8. The critical heat flux, or burnout, corresponds physically to the drying out of the thin liquid film on the wall in annular flow (hence the term dryout). Direct confirmation of this effect was achieved by Hewitt et al. in 1963. The flow rate in the liquid film was measured by drawing it off through a porous section of wall. The critical heat flux was shown to correspond to the liquid film flow rate falling to zero. Beyond the dryout position, there is a tendency for the vapor, being directly in contact with the wall, to superheat.
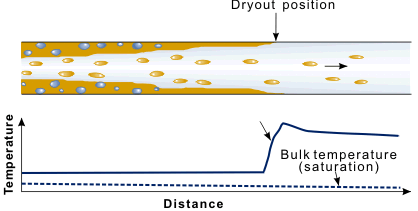
Figure 8. In high quality flows the critical heat flux is equivalent to dryout of the annular liquid film.
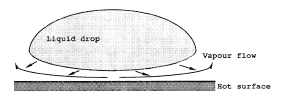
There is a sudden increase in the wall to bulk temperature difference once the critical heat flux (burnout or dryout) point is passed. The size of the temperature jump is likely to be larger if heat flux is the controlling parameter, rather than surface temperature. Although there are still liquid drops present in the flow, there is evidence that they do not contribute much to the heat transfer. At these high wall temperatures, vapor formation, as the drop approaches the wall, may be sufficient to prevent contact (Figure 9). The flow of vapor out of the narrow gap creates a pressure drop. The raised pressure in the gap prevents contact. For the simple case of a drop resting on a hot horizontal surface, this phenomenon is known as the Leidenfrost effect (observed by Leidenfrost in 1756) (see article on Leidenfrost Phenomena). In fact, unless the surface is slightly dish-shaped, the drop will not stay there. Drops of water spilt on a very hot surface, such as the heating element of an electric cooker, shoot off in all directions. They are not in contact with the solid surface; they are floating on a film of vapor. These topics are further discussed in the article in Post-Dryout Heat Transfer.
Although the mechanism at the critical heat flux in flow boiling may often be dryout of the annular liquid film, there are other possibilities. At sufficiently high heat fluxes the critical heat flux may occur in low quality or even subcooled flows. Bulk liquid continues past the critical heat flux point, separated from the wall by a vapor film, i.e., a type of film boiling.
The above discussion of forced convection boiling implicitly assumed vertical flow. Provided the flow rate is reasonably high, all parts of the tube are still well wetted in horizontal flow, and the heat transfer behavior is very similar. At sufficiently low flow rates in horizontal tubes, the liquid will tend to flow along the bottom of the tube and, roughly speaking, only the bottom wetted portion of the circumference will be cooled. Burnout is likely to occur earlier and will appear on the top of the tube. Even at higher flow rates, premature burnout may occur in annular flow if the annular film becomes thinner on the top of the tube.
REFERENCES
Abbassi, A., Alem Rajabi, A. A., and Winterton, R. H. S. (1989) Effect of confined geometry on pool boiling at high temperature, Experimental Thermal and Fluid Science 2:127–133. DOI: 10.1016/0894-1777(89)90026-5
Alem Rajabi, A. A. and Winterton, R. H. S. (1988) Liquid-solid contact in steady-state transition pool boiling, Int. J. Heat and Fluid Flow 9:215–219. DOI: 10.1016/0142-727X(88)90074-4
Berenson, P. J. (1961) Film boiling heat transfer from a horizontal surface, Trans. ASME J. Heat Transfer 83:351–358.
Bromley, L. A. (1950) Heat transfer in stable film boiling, Chem. Engng. Progress 46:221–227.
Chen, J. C. (1966) Ind. Eng. Chem. Process Design and Development, 5:322–329.
Cheng, S. C. Ng, W. W. L., and Heng, K. T. (1978) Measurements of boiling curves of subcooled water under forced convective conditions, Int. J. Heat and Mass Transfer 21:1385–1392. DOI: 10.1016/0017-9310(78)90202-8
Cooper, M. G. (1984) Saturation Nucleate Pool Boiling — A Simple Correlation. 1st U.K. National Conf. on Heat Transfer, Inst. Chemical Engineers 785–793.
Gaertner, R. F. (1965) Photographic study of nucleate pool boiling on a horizontal surface, J. Heat Transfer 87:17–29.
Hewitt, G. F., Kearse, H. A. P., Lacey, M. C., and Pulling, D. J., (1965) Burnout and nucleation in climbing film flow, Int. J. Heat and Mass Transfer 8:793–814. DOI: 10.1016/0017-9310(65)90025-6
Lienhard, J. L. (1981) A Heat Transfer Textbook, Prentice-Hall, New York.
Liu, Z. and Winterton, R. H. S. (1991) A general correlation for saturated and subcooled flow boiling in tubes and annuli based on a nucleate pool boiling equation. Int. J. Heat and Mass Transfer 34:2759–2766. DOI: 10.1016/0017-9310(91)90234-6
Nukiyama, S. (1966) The maximum and minimum values of the heat Q transmitted from metal to boiling water under atmospheric pressure, Int. J. Heat and Mass Transfer 9:1419–1433. DOI: 10.1016/0017-9310(84)90112-1
Zuber, N. (1958) On the stability of boiling heat transfer, Trans. ASME, 80:711–720.
ADDITIONAL REFERENCES
The following are three recently published books on the subject:
J. G. Collier and J. R. Thome (1994) Convective Boiling and Condensation, 3rd edition, Oxford.
K. Stephan (1992) Heat Transfer in Condensation and Boiling, Springer-Verlag.
P. B. Whalley (1987) Boiling, Condensation and Gas–Liquid Flow, Oxford.
References
- Abbassi, A., Alem Rajabi, A. A., and Winterton, R. H. S. (1989) Effect of confined geometry on pool boiling at high temperature, Experimental Thermal and Fluid Science 2:127–133. DOI: 10.1016/0894-1777(89)90026-5
- Alem Rajabi, A. A. and Winterton, R. H. S. (1988) Liquid-solid contact in steady-state transition pool boiling, Int. J. Heat and Fluid Flow 9:215–219. DOI: 10.1016/0142-727X(88)90074-4
- Berenson, P. J. (1961) Film boiling heat transfer from a horizontal surface, Trans. ASME J. Heat Transfer 83:351–358.
- Bromley, L. A. (1950) Heat transfer in stable film boiling, Chem. Engng. Progress 46:221–227.
- Chen, J. C. (1966) Ind. Eng. Chem. Process Design and Development, 5:322–329.
- Cheng, S. C. Ng, W. W. L., and Heng, K. T. (1978) Measurements of boiling curves of subcooled water under forced convective conditions, Int. J. Heat and Mass Transfer 21:1385–1392. DOI: 10.1016/0017-9310(78)90202-8
- Cooper, M. G. (1984) Saturation Nucleate Pool Boiling — A Simple Correlation. 1st U.K. National Conf. on Heat Transfer, Inst. Chemical Engineers 785–793.
- Gaertner, R. F. (1965) Photographic study of nucleate pool boiling on a horizontal surface, J. Heat Transfer 87:17–29.
- Hewitt, G. F., Kearse, H. A. P., Lacey, M. C., and Pulling, D. J., (1965) Burnout and nucleation in climbing film flow, Int. J. Heat and Mass Transfer 8:793–814. DOI: 10.1016/0017-9310(65)90025-6
- Lienhard, J. L. (1981) A Heat Transfer Textbook, Prentice-Hall, New York.
- Liu, Z. and Winterton, R. H. S. (1991) A general correlation for saturated and subcooled flow boiling in tubes and annuli based on a nucleate pool boiling equation. Int. J. Heat and Mass Transfer 34:2759–2766. DOI: 10.1016/0017-9310(91)90234-6
- Nukiyama, S. (1966) The maximum and minimum values of the heat Q transmitted from metal to boiling water under atmospheric pressure, Int. J. Heat and Mass Transfer 9:1419–1433. DOI: 10.1016/0017-9310(84)90112-1
- Zuber, N. (1958) On the stability of boiling heat transfer, Trans. ASME, 80:711–720.