A binary system is a particular case of the more general Multicomponent System in which only two components are present. Such systems are sometimes called mixtures, with the implication that both substances present are to be treated on equal footing, and sometimes as solutions, in which the excess component is called the solvent and the other, the solute. The thermodynamics, however, contain much in common and for the most part, one need not distinguish between them.
The general characteristic of binary systems is that when, say, two liquids are mixed together at the same pressure and temperature, the extensive properties (volume, enthalpy, entropy, etc.) of the mixture are not the sum of those of the unmixed components. Nevertheless, it is convenient to ascribe part of the volume, say, to component 1 and the rest to component 2. There is no unique way in which this can be done, but one way which is useful to thermodynamics is via partial molar quantities. For example, the partial molar volume of component i is defined as:

where ni is the amount of component i present in the mixture, and the nj constraint to the partial derivative means that all amounts of components other than i, are to remain fixed. On this basis, the total volume of the (binary) mixture is:

A similar set of equations exists for all other extensive thermodynamic quantities.
Expressed in molar terms, this last equation becomes:

where 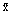 are the mole fractions. If we differentiate this equation, partially with respect to each of the mole fractions and invoke the Gibbs-Duhem Equation, it becomes:
are the mole fractions. If we differentiate this equation, partially with respect to each of the mole fractions and invoke the Gibbs-Duhem Equation, it becomes:
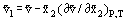

providing a means of determining the partial molar quantity from experimentally observable results. A similar set of equations can be obtained for the other extensive thermodynamic properties, but the quantities involved are usually less experimentally accessible.
One partial molar quantity of particular importance is the Chemical Potential:

where G is Gibbs free energy.
The thermodynamics of binary systems is intimately linked with the desire to predict the thermodynamic properties of such systems. There exists a hierarchy of methods for making these predictions, ranging from the extremely simple, but limited in scope, to the highly complex, but of wide applicability.
The simplest case is that of the ideal mixture. This is defined as one for which:

for each component i in the mixture. (μi is the chemical potential of component i in the mixture of mole fraction composition  , μjc is the chemical potential of pure component i.)
, μjc is the chemical potential of pure component i.)  is the universal gas constant.
is the universal gas constant.
It follows from this definition that: the equation for Gibbs free energy, entropy, enthalpy and volume, respectively are:


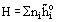
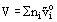
where  ,
,  , and
, and  are the molar entropies, enthalpies and volumes of the pure components i and ni are the number of moles of each component present in the mixture. Note that whereas enthalpies and volumes are additive, this is not true for G and S. It can be shown from the above that Cp and Cv, the heat capacity at constant pressure and at constant volume, respectively, are also additive.
are the molar entropies, enthalpies and volumes of the pure components i and ni are the number of moles of each component present in the mixture. Note that whereas enthalpies and volumes are additive, this is not true for G and S. It can be shown from the above that Cp and Cv, the heat capacity at constant pressure and at constant volume, respectively, are also additive.
In the gas phase, it is often sufficient to work at a low enough pressure, say ambient, in order for the approximation of an ideal mixture to be adequate. However, more stringent conditions apply for the liquid phase. In general, the ideal mixture approximation only applies when the molecular species present are very similar.
When the ideal mixture approximation is inadequate, more precise expressions must be used for the partial molar quantities. See, for example, Activity Coefficient, Fugacity.