Bessel’s series is the expansion of a function f(x) square integrable and weight integrable in the interval (0, a) into a series in terms of Bessel Functions of order λ, Jλ(μkax), where k = 1 ÷ ∞

Here, μk are the positive roots of Bessel’s function Jλ arranged in an increasing order (λ > -½). The coefficients of a series have the form:

A system of Bessel’s functions is orthogonal to weight x and is complete on the interval (0, a). This means that a sequence of partial sums of the series converge on the interval (0, a) in a root-mean-square (with weight x) to the function f(x).
The orthogonality relationships for the Bessel function have the following form:


A Bessel’s series for a function f(x) can be obtained by expanding a function 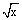 f(x) into a Fourier series with respect to an orthogonal system
f(x) into a Fourier series with respect to an orthogonal system 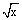 Jλ(μkx/a); k = 1 ÷ ∞, which makes it possible to transfer onto the Fourier-Bessel series the results known for the Fourier series from orthogonal functions.
Jλ(μkx/a); k = 1 ÷ ∞, which makes it possible to transfer onto the Fourier-Bessel series the results known for the Fourier series from orthogonal functions.