Aerodynamics is the branch of hydrodynamics that deals with the laws of air motion and with the forces acting on the surfaces of streamlined bodies. Aerodynamics generally studies motion with velocities which are far short of the sound velocity (340 m/s, 1200 km/h). This is in contrast to gas dynamics, which deals with the motion of compressible gaseous media and with their interaction with solids.
One of the major problems facing aerodynamics is to determine forces acting on bodies when they move through an atmosphere. It is, therefore, a part of the science concerned with external flows. Nevertheless, the methods and results of classical “force” aerodynamics also enjoy wide use in investigating heat transfer between a body and a fluid flowing around the body and in analyzing the structure of single- and multi-phase flows.
Aerodynamics developed in response to the demands of practical applications. Aerodynamics as a branch of hydrodynamics appeared early in the 20th century with the advent of aircraft construction. The aerodynamics of aircraft and, in general, of a flying vehicle deals with the definition of aerodynamic forces and moments acting on the entire vehicle and on its parts, wing, fuselage and tail unit.
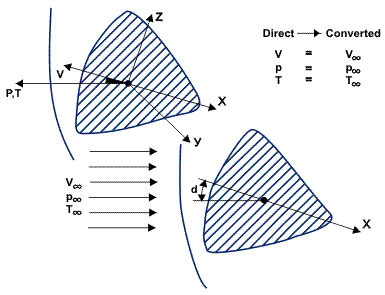
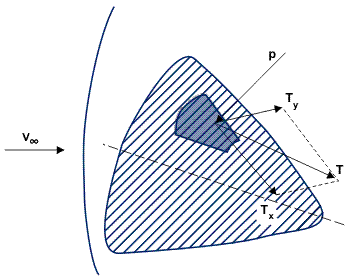
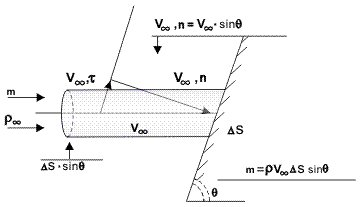
Depending on the methods of solving aerodynamics problems, these are classified as experimental or theoretical. The basis for the experimental methods is the reversibility principle of motion, which states that “the force acting on a body when the fluid moves around it with constant velocity is equivalent to the force which a body experiences in uniform and translatory motion in a stationary atmosphere.” In this case, it is obvious that the velocity V of flight must correspond in magnitude and direction relative to the body axis, with the velocity of an incoming (converted) flow V∞ (Figure 1). The effect of the gaseous flow around the body manifests itself as a pressure p and a friction (shear force) τ (Figure 2). The pressure p is directed along the normal to an elementary area on the surface of the body, and the friction (shear) τ lies in the plane tangent to the body surface. The friction results from the viscosity of the air flow and from the adhesion of particles of gas to the body surface.
The pressure forces and the frictional forces acting on the surface of a body can be reduced to the resultant
 of these forces, called the aerodynamic force, and to a couple with a moment
of these forces, called the aerodynamic force, and to a couple with a moment
 , called the aerodynamic moment. The aerodynamic moment plays a leading role in designing air vehicles, defining their stability and controllability. Both the aerodynamic force
, called the aerodynamic moment. The aerodynamic moment plays a leading role in designing air vehicles, defining their stability and controllability. Both the aerodynamic force
 and the aerodynamic moment
and the aerodynamic moment
 can be resolved into components in a rectangular Cartesian coordinate system, associated either with the vector of flight velocity
can be resolved into components in a rectangular Cartesian coordinate system, associated either with the vector of flight velocity
 (wind coordinate system) or with the body itself (body axis system).
(wind coordinate system) or with the body itself (body axis system).
In the wind coordinate system, the force directed along the flow opposite to the direction of motion is called the drag force X; the force perpendicular to it and lying in the vertical plane, the lift force Y; and the force perpendicular to both, the lateral force Z. The projections of the moment
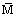 onto the axes of the body axis coordinate system are called the roll moment Mx, the yawing moment My and the pitching moment Mz.
onto the axes of the body axis coordinate system are called the roll moment Mx, the yawing moment My and the pitching moment Mz.
The shape of a body which when it moves in air results in a lift exceeding the force which impedes the flight (for instance, gravity) is called the aerodynamic profile (or lifting surface). The lift-drag ratio is called the aerodynamic efficiency K. Aerodynamic efficiency depends on the profile of the air vehicle. Thus, the aerodynamic efficiency of the spherical spacecraft Vostok, piloted by Yu. A. Gagarin, was close to zero. The spacecrafts Soyuz and Apollo were symmetrical vehicles of low efficiency (of the order of 0.3). The aerodynamic efficiency of such space vehicles as the Space Shuttle and Buran is considerably higher. Aerodynamic efficiency also depends on the angle of attack α, formed by the vehicle axis or the chord of its wing and the direction of velocity of the undisturbed flow of air.
To simulate the motion of a body in a stationary air, special experimental set-ups called wind tunnels are used. The simulation method is based on the similarity theory, according to which the aerodynamic forces and moments acting on a flying vehicle can be determined from the test results of a small-scale model of this object. In this case, conditions which will ensure the possibility of transferring the results obtained on a laboratory set-up to a full-scale object should be met.
In addition to the geometrical similarity of the natural object and the model, the Mach number and the Reynolds number found from the parameters of the incoming flow must be the same. The results of measurement of forces and moments are represented in the form of dimensionless ratios:
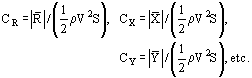
The dimensionless quantities CR, CX and CY, …, which characterize aerodynamic forces and moments acting on the body moving through a gaseous atmosphere are called the aerodynamic coefficients, CX being the drag coefficient (see also Drag Coefficient).
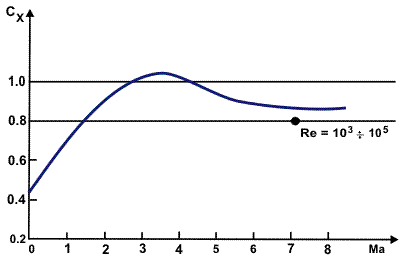
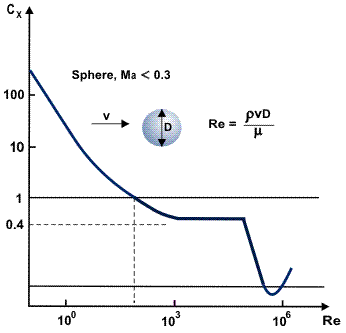
A typical dependence of aerodynamic coefficients on the Mach and Reynolds numbers is given in Figures 3, 4. The use of the velocity head of the air flow (ρν2/2) and of typical cross-sectional area S of the vehicle is of prime importance for making and planning aerodynamic investigations. The aerodynamic force can vary by several orders of magnitude, while the aerodynamic coefficient may remain constant. In this case, the possibility exists of generalizing as single parameters all varieties of vehicles and their models and of obtaining convenient relationships for predicting coefficients.
For subsonic velocities pf large-sized vehicles, the aerodynamic coefficients depend mainly on the shape of the vehicle and on the angle of attack. In general, the achievement of two similarity criteria, the Mach and the Reynolds number, in wind tunnels is next to impossible. Because of a reduction of the model dimensions, in order to satisfy the Reynolds number condition, there is a need either to increase the velocity V (but then the Mach number condition is not met) or to increase the density of gas or to decrease the viscosity of air. In practice the problem can be overcome if the aerodynamic coefficient is independent of Re or Ma over a sufficient range. Thus, the drag coefficient of a sphere is practically independent of the Reynolds number in the range of 103 < Re < 106 (see Figures 3, 4).
The presentation of test results as functional equations between dimensionless similarity criteria, on the one hand, reduces the number of independent variables, and on the other, allows us to find the range of self-similarity and thus to increase the reliability of transferring the laboratory test data to natural conditions.
There has been a tremendous growth in modern theoretical aerodynamics. Based on the hypothesis suggested by Prandtl in 1904, the entire space around the streamlined body is divided into two areas: the boundary layer (see Boundary Layer), where the effect of air viscosity and thermal conductivity and also of thermal condition of the body is significant; and the area outside the boundary layer, where the air can be considered as an ideal gas (see Inviscid Flow).
Analyzing the basic laws of hydrodynamics (see Conservation Laws) formulated in the form of equations by Euler, Lagrange, Stokes, and Prandtl, one can obtain the solution for a large number of problems on the motion of a body through the atmosphere of the Earth and of the other planets. In many cases, however, the intricate design of the vehicle and the proximity of the Earth surface presents difficulties in the theoretical analysis even with the use of modern computers. Therefore, approximate methods of analysis are extensively employed.
The first theoretical definition of the law of the atmosphere resistance through which a body moves was formulated by Isaac Newton, who suggested that it is associated with the impact of particles against the frontal surface of the body. He showed that resistance is proportional to the square of the body velocity and the angle of inclination θ of its surface to the direction of motion (Figure 5). In this case, for instance, for a wedge with an apex angle 2θ we have CX = 2 sin2θ. For bodies of irregular shape, the quantity CX can be estimated by approximating the real contour of the body to a certain cone or wedge. Therefore, for a cylinder with a plane end face, CX = 2 and for a sphere, CX = 1. The experimental data, however, are in good agreement with the Newton model only for supersonic velocities. Nevertheless, Newton laid the foundation for explaining the problems of aerodynamics on the basis of the laws of mechanics.
Modern aerodynamics has gained experience in defining the aerodynamic characteristics of a large set of simple casings and wings, and also of their combinations. This substantiated the proposed principle of separating a flying vehicle into components or constituents for which the definition of aerodynamic coefficients presents no problem, and integral parameters are calculated by the additivity principle. In some cases, a second approximation is used in which interference corrections are defined.
This principle is also used as the basis for the calculation of nonstationary aerodynamic characteristics using additional terms of the series defining the aerodynamic characteristics reflecting the nonstationary flows.
Aerodynamic design has assumed an independent significance in connection with the production of vehicles of the “flying-wing” type. Of special interest is the study of casings of body-of-revolution type, because among these are the majority of rocket-type units. As to the velocities of irregular shape, experimentation shows that as the flight velocity increases (especially in the supersonic range), the effects of the interference interaction become less significant. This is because the zones of mutual effect become narrower. It should be remembered, however, that this conclusion cannot be extended to heat transfer problems.
Modern controlled flying vehicles have numerous aerodynamic, gasdynamic (jet) and combined controls. To find the control force is the key element in the aerodynamic calculation; because in this case, the arrangement and flying characteristics of the vehicle are defined. Nevertheless, this problem is rather intricate and can often be solved only by experimentation.
On increasing the velocity of flight and on its approach to sound velocity, consideration must be given to the compressibility of the atmosphere. The supersonic flight of the body is characterized by a number of peculiarities: shock waves arise (see Shock Tubes) which increase the drag, the flying body warms up through air friction and due to radiation from the highly compressed gas behind the shock wave. In flights with high supersonic (or hypersonic) velocity, dissociation and ionization of air molecules occur. All these problems are usually referred to a branch of hydrodynamics called “gas dynamics.”
A broad field of non-aviation applications of aerodynamics represents a science called industrial aerodynamics. It deals with the problem associated with the design of blowers, wind motors, fans and air conditioners and also ejectors.
A blower is designed to compress and to feed air at moderate pressures. The air produced by blowers is mainly consumed in ferrous metallurgy. To produce 1 ton of pig iron, 2 tons of compressed air at a pressure of up to 0.5 MN/m2 is required. Modern blowers have compressors driven by gas or steam turbines, with a power of 20 MW and higher. Their capacity is 5000-10,000 m3/min of air at a temperature of 500°C.
A fan is the machine designed to deliver air or other gases at an excess pressure not higher that 12-15 kN/m2 (0.12-0.15 atm). Fans serve to ventilate buildings and mines, to deliver air to boiler rooms and furnace apparatuses, to remove flue gases, to dry materials, to cool machine parts and mechanisms, to produce air screens, to transport pheumatically loose and fibrous material, etc.
The centrifugal or radial fan has a wheel located in a volute casing; on rotating the wheel, the gas delivered through an inlet enters into the channels between the plates and, acted upon by the arising centrifugal force, moves into the volute casing and is directed into the outlet along the tangent to the casing (Figure 6).
The axial-flow fan has a blade wheel located in a cylindrical casing (Figure 7). When the wheel rotates, the supplied gas moves in the axial direction. The axial-flow fan, as compared to the centrifugal one, is more simple, has a higher efficiency, but cannot achieve high pressures. To increase the fan capacity and pressure, the fans are connected in either series or in parallel.
As a preliminary estimate of the optimum conditions for fan operation, we can use the generalized plot given in Figure 8. Presented in the pressure p [N/m2] ѕ capacity
 [m3/s] coordinate system are the angular velocities ω [rad/s] and the efficiency η. From the given
[m3/s] coordinate system are the angular velocities ω [rad/s] and the efficiency η. From the given
 and p, we can find the point on the plot which defines the required velocity ω and the efficiency η, from which the required power is calculated.
and p, we can find the point on the plot which defines the required velocity ω and the efficiency η, from which the required power is calculated.
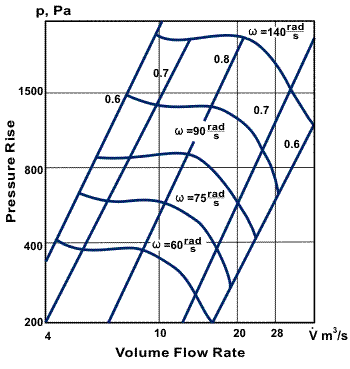
Figure 8. Angular velocity (ω) and efficiency (η) for fans providing a given volume flow rate
 at a given pressure rise (p).
at a given pressure rise (p).
The air screw or propeller can also be used as the motor for subsonic aircraft, helicopters or transport air cushion vehicles (ground-effect machines, hovercraft). Two methods of air cushion formation are recognized: the static and dynamic. In the static method, the pressure in the air cushion is built up by a fan or a compressor, in the dynamic method, it is created by the relative velocity of the air flow. The schemes of air cushion formation that have enjoyed the widest application are the: (a) chamber; (b) nozzle; (c) slit; and (d) wing (Figure 9).
In a chamber scheme, the lift is produced by the static pressure of the air delivered by the fan under the casing base. The chamber is raised by the lift and the air flows out through a clearance formed between the chamber edges and the bearing surface. Since the efflux area is rather large, a considerable body of air is required even with considerably small clearances.
In a nozzle scheme, the air cushion is formed because of the air efflux from the nozzle located along the periphery of the nozzle unit. The lift is the sum of the static pressure at the cut of the nozzle unit and the reactive force of the air efflux from the nozzle. This scheme allows larger clearances between the apparatus and the bearing surface with smaller air expenditure.
In a slit scheme, the air cushion is formed in a thin clearance through which the air flows out in all directions. In order to form the slit clearance, both the lifting and the bearing surfaces are shaped. An increased pressure in the air cushion is maintained due to the viscosity of the air passing through the slit.
In a wing scheme, the air cushion is formed under the wing of the air vehicle when it moves with an angle of attack near the bearing surface.
The air ejector is the device in which the total pressure of air flow is increased under the action of the jet of another high-pressure flow. The energy from one flow is transferred to another flow through turbulent mixing. The ejector is simple in design, can operate in a wide range of change of gas parameters, permits easy control of the operating process and a change from one mode of operation to the other. Depending on the purpose, ejectors are made by different ways.
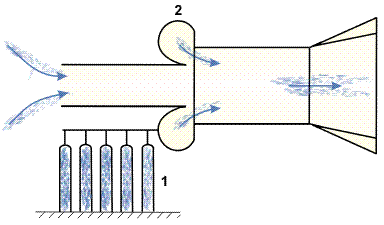
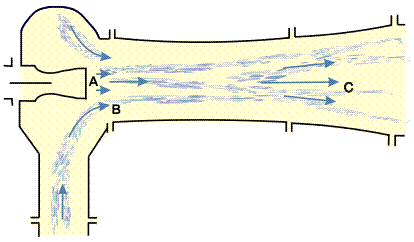
In some wind tunnels, a number of ejectors functioning as pumps may be set in series as illustrated in Figure 10. Bottles (1) contain air at high pressure. The ejector (2) sucks in atmospheric air as shown in the figure. This leads to a volumetric flow rate
 which is many times the flow from the bottles, thus allowing larger models to be tested.
which is many times the flow from the bottles, thus allowing larger models to be tested.
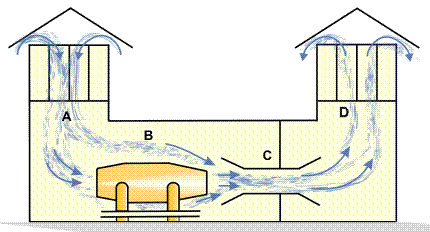
Figure 11 shows a schematic diagram of a jet engine used to feed an ejector to create airflow in the test stand for the engine. The exhaust gas jet flowing out of the propulsive nozzle draws in the air from the pit A into the ejector C, thus ensuring ventilation of the stand location and cooling of the engine B. Hot gases intermix with the atmospheric air, which results in the drop of the gas temperature in the pit D and improves the conditions of the noise suppressor operation.
Finally, in vacuum systems, the vacuum ejector functions as an exhauster (Figure 12). Especially high vacuum (down to one millionth of an atmosphere) can be obtained, mercury vapor is used as the ejecting gas. The ejecting A and the ejected B gas enter into a mixing chamber as two separate flows: in general, they can differ in chemical composition, velocity, temperature and pressure. Mixing of flows results in the equalizing of gas parameters across the entire section C of the jet outlet section. For other versions of ejector application, in condensation systems of steam power plants, in particular, see Jet Pumps and Ejectors