Methods used for drop size measurement can be classified under four main groups: photographic methods, optical methods, sampling methods, electrical contact methods and acoustic methods.
These methods are widely-used and they allow a wide range of information to be obtained as size, form and concentration in a given flow field. Drop trajectories and breakdown and coagulation phenomena can also be studied. High-speed cameras and objectives with high resolution are utilized and stroboscopic light sources are often used to light the zone being investigated. Localized lighting is often obtained using light guides.
The optical methods which have gained ground are: method of scattering indicatrix, method of small angles, polarization method of scattering light, method of light attenuation and methods related to Laser-Doppler anemometry.
The method of scattering indicatrix is used for measuring drops within the radius range of 0.01 to 100 μm. When a light beam is incident on an individual particle, the particle becomes a second source of radiation, scattering light all around in a way characterized by the scattering indicatrix—which is defined as the distribution of light scattered over all solid angles relative to the direction of the incident beam.
The angular distribution of light scattering from the particle depends on its radius. If the particle radius rd is considerably less than the wavelength of the incident light λ, the scattering indicatrix is symmetric relative to the plane that is perpendicular to the incident beam. The scattering indicatrix changes considerably for larger particles (rd ≥ λ). In this situation, it is not symmetric and scattering in the direction of the incident beam predominates.
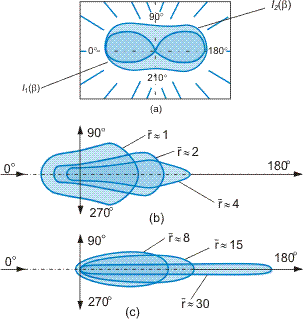
Typical indicatrices as calculated for different diameters of water drops are presented in Figure 1. Figure 1a shows light scattering by particles with very small radius
 (where
(where
 is the dimensionless drop radius). The curve I2(β) represents the component of scattering light in the plane parallel to the observed plane and the curve I1(β), the plane perpendicular to it. Figure 1b shows the growing asymmetry of light scattering in the plane normal to the incident beam as drop size increases. The ratio of scattered light intensities measured for two angles relative to the plane perpendicular to the incident beam is a function of rd and can be used for determining rd. Figure 1c represents the change in the scattering indicatrix with an increase in particle size. The asymmetry grows, the tongue of the scattering indicatrix becomes narrow and is extended and light reflection is attenuated (at
is the dimensionless drop radius). The curve I2(β) represents the component of scattering light in the plane parallel to the observed plane and the curve I1(β), the plane perpendicular to it. Figure 1b shows the growing asymmetry of light scattering in the plane normal to the incident beam as drop size increases. The ratio of scattered light intensities measured for two angles relative to the plane perpendicular to the incident beam is a function of rd and can be used for determining rd. Figure 1c represents the change in the scattering indicatrix with an increase in particle size. The asymmetry grows, the tongue of the scattering indicatrix becomes narrow and is extended and light reflection is attenuated (at
 , reflected light is equal to 1/10 of the transmitted light; at
, reflected light is equal to 1/10 of the transmitted light; at
 , the ratio is 1/10000).
, the ratio is 1/10000).
The intensity of light scattering by a particle at different angles to the incident beam direction is determined by the equation

where rd is the drop radius; m, the refractive index of the particle material; λ, the wave length of the incident light; z, the distance from the particle to the detection device; I0, the incident light intensity; and β, the angle to incident beam direction. If there are n particles with different sizes with the volume sampled V, the expression for Ir reduces to the form

where

and f(r) is the distribution function of particle size.
Secondary scattering need not be accounted for until the distance between particles is less than their radius; this corresponds to a range of liquid fractions of 0 < εL < 6%. At high liquid fractions (εL ≈ 20-30%), it is necessary to take into account secondary scattering.
The method of small angles is used for determining particle sizes ranging from 1 to 300 mm. It is based on measurement of the scattering indicatrix of radiation at small angles. The limitations of this method are two-fold, as follows:
Particle concentration in the translucent volume cannot be too high; otherwise the effect of secondary scattering becomes significant.
The thickness of the translucent volume is limited by the value δ = lnI'0/I0 ≤ 0.3, where I'0 is the transferred light intensity without scattering particles and I0, light intensity transferred through the investigated volume with scattering particles.
The polarization of scattered light in the visible part of the spectrum, for range of drop radius rd = 0.05-0.025 μm and observation angle β = 90°, changes smoothly with rd. Drop radius is determined by measuring the intensity of the polarized light. As a result of the presence of particles, the intensity maximum for the polarized light is shifted in the direction of angles more than 90°.
According to Bouguer's law, light beam intensity I on outlet from dispersed medium is bounded to the intensity I0 on inlet by dependence

where k is the index of light beam attenuation and l is the path length of the light beam.
Index k takes account of the scattering (ks) and absorption (ka) of light in medium

For λ = 0.5 μm, light absorption by water particles is very small and it can be supposed that k ≈ ks. The equation of light attenuation in the dispersed medium stress has the form

where kλπr2 characterizes the effective scattering surface for each particle with radius r and n is the number of particles per unit volume. This method measures, at the same point in a two-phase medium, the attenuation of radiation with wavelengths λ1 and λ2 and stress, determines the ratio kλ1/kλ2. One can then find the particle size using the relationships

and

.
A number of methods for drop size determination based on laser/Doppler anemometry have been developed [see Hewitt (1982) for a review]. These methods use a variety of principles, which include:
Measurement of "visibility", which is the ratio of the maximum to minimum value of the fluctuating signal in the Doppler burst.
Measurement of the amplitude of the Doppler burst from a given drop.
Measurement of the phase behavior of the Doppler signal ("phase Doppler anemometry").
Though quite expensive, the last of these methods appears to be finding the widest use.
The sampling method is realized by using glass plate that is coated with a layer of viscous liquid and is inserted briefly into the flow. Drop sizes are determined from photographs or with the aid of a microscope. In an alternative version of this method, the plate is covered by magnesium oxide. Pits are formed in the soft magnesium layers by the drop impact and their size is related to drop size.
Water drops can also be collected and inserted into oil for determination of their sizes with the aid of a microscope. The drops can also be frozen when they are inserted into a low-temperature liquid. In this case, the particle size distribution can be determined with the help of sieves.
Wicks and Dukler have proposed a method that is based on recording the drop contact frequency between an inline pair of needles where tips have an adjustable distance. The electric contact between needles arises if the drops touch them simultaneously. The counter is used to monitor closure frequency. The distance between the needles is changed and the closure frequency measured again. Drop size distribution can be determined from the obtained results, using probability theory. In the case of high velocity flow, the amplitudes of useful pulses are small and the effect of false pulses, which are created by charged drops that do not close the electrodes, is important. Circuits with amplitude limitation are used to exclude the effect of these pulses. Useful pulses that have amplitudes less than critical value are eliminated. This method can be used at a flow velocity of more than 40-50 m/s. At low velocity, the liquid drop can adhere to the electrodes and the accuracy of measurement decreases sharply.
A circuit with high-frequency correction has been applied to measure the drop distribution at very high flow velocities (up to 180 m/s). Upon contact of the electrodes with the drop, the current increases in the first winding of a transformer. The pulse number is determined by a counter. This method allows the use of different designs of clocks. The drop size distribution function is determined by the following equation:

where
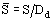 is the distance between the electrodes; Dd, the drop diameter; f, the closure frequency; S, the cross-section area of the investigated volume;
is the distance between the electrodes; Dd, the drop diameter; f, the closure frequency; S, the cross-section area of the investigated volume;
 , where Dkm is the maximum drop diameter.
, where Dkm is the maximum drop diameter.
A comparison of the different methods for drop size measurement shows that their usability depends on flow conditions. For example, at high velocities (150-180 m/s), the optical and electric methods give similar results. At small velocities, the methods of Wicks-Dukler, optical method and method of prints give compatible results.
REFERENCES
Hewitt, G. F. and Hall-Taylor, N. S. (1970) Annular Two-Phase Flow. Pergamon Press, Oxford.
Hewitt, G. F. (1982) Measurement of Drop and Bubble Size. Chapter 10.2.2.6 of the Handbook of Multiphase System (Ed. G. Hetsroni). McGraw Hill, New York.