EMISSIVITY OF TWO-PHASE COMBUSTION PRODUCTS IN A SOLID-PROPELLANT ROCKET ENGINE
Following from: Radiation heat transfer in a solid-propellant rocket engine.
In this article, we consider the effect of particle size, volume fraction, and temperature on spectral and integral emissivity of an isothermal volume of combustion products. Following Dombrovsky (1996), the main results are given for the simplest geometrical model of a homogeneous plane-parallel layer of the medium. This model has been employed in early papers by Dombrovsky and Ivenskikh (1973) and Dombrovsky (1974, 1976). One can find a similar problem statement in papers by Pearce (1978), Modest (1981), Popov (1984), Der and Nelson (1985), Kuzmin et al. (1989), Lee (1989), Brewster (1989), and Thynell (1990), where infinite cylindrical volume was considered side by side with the plane-parallel layer. Papers by Pearce (1978), Der and Nelson (1985), and Kuzmin et al. (1989) are also concerned with the thermal radiation of aluminized propellant combustion products. The simple model of isotropic scattering was assumed by Pearce (1978). More accurate calculations for anisotropic scattering were performed by Dombrovsky and Ivenskikh (1973) and Der and Nelson (1985). The results by Dombrovsky and Ivenskikh (1973) are more general, i.e., Der and Nelson (1985) performed calculations at only one radius of particles, a = 2.5 μm, without taking into account any spectral dependence of aluminum oxide optical constants. A simplified approximate method of the spectral emissivity calculations for combustion products of an aluminized propellant has been proposed by Kuzmin et al. (1989). The papers mentioned do not give the complete notion about the main thermal radiation regularities for two-phase combustion products under consideration. Following the monographs by Dombrovsky (1996) and Dombrovsky and Baillis (2010), a complete discussion of thermal radiation from a cloud of molten aluminum oxide particles is presented in this article.
Consider the thermal radiation of a layer containing monodisperse droplets of aluminum oxide melt. Obviously, the spectral hemispherical emissivity of the layer of thickness H depends on the particle radius a, temperature T, and mass of the particles per unit area of the disperse layer surface ρH, where ρ is the mass concentration of particles. Computational results for the spectral emissivity ελ at T = 3000 K are presented in Fig. 1. Calculations were made by use of the DP1 analytical solution (see the article, “The simplest approximation of double spherical harmonics”). Similar dependences for the values of T = 2500 K and 3500 K can be found in the book by Dombrovsky (1996). The density of an aluminum oxide melt was determined by use of linear approximation of the experimental temperature dependence (Kirshenbaum, and Cahill, 1960; Mitin and Nagibin, 1970) [see Eq. (8) from the article, “Near-infrared properties of droplets of aluminum oxide melt”].
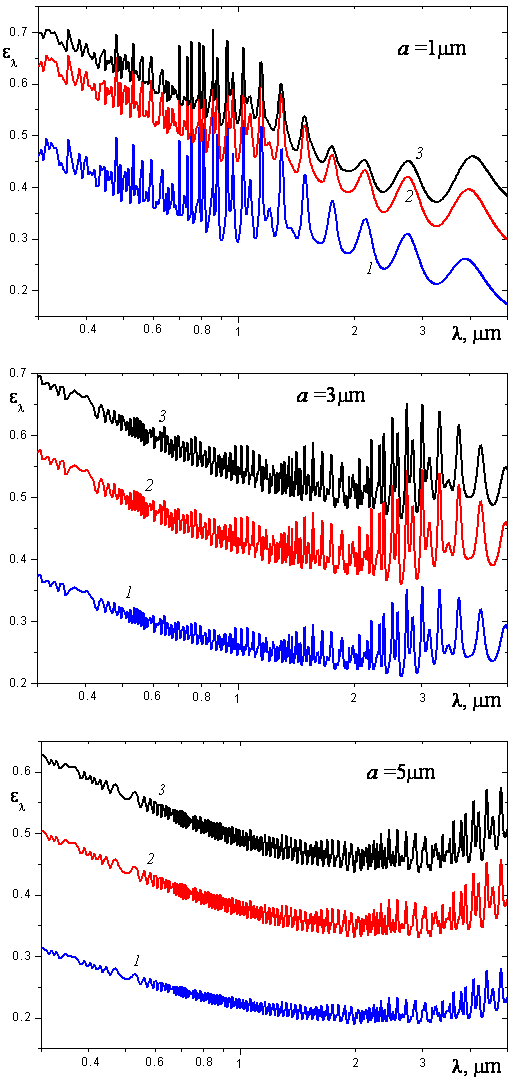
Figure 1. Spectral hemispherical emissivity of a plane-parallel layer containing monodisperse alumina particles at T = 3000 K: 1-ρH = 5g/m2; 2-10g/m2; 3--20g/m2
One can see that the emission spectrum depends on the particle radius. In any case, the greatest emissivity takes place in the visible spectral range where the diffraction parameter x = 2πa/λ is large and transport albedo of a single particle ωtr = Qstr/Qtr is relatively small (see article, “Near-infrared properties of droplets of aluminum oxide melt”). Strong oscillations of the curves ελ(λ) observed at the wavelength λ ≈ a can also be explained by consideration of single particle radiative properties. The results for integral hemispherical emissivity defined as

are presented in Fig. 2.
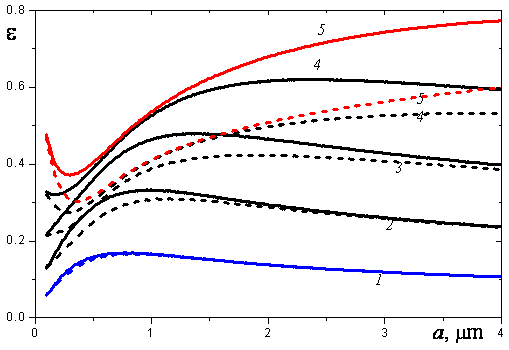
Figure 2. Integral hemispherical emissivity of a plane-parallel layer containing monodisperse alumina particles at T = 3000 K (dashed lines--by ignoring the anisotropy of scattering): 1-ρH = 2 g/m2; 2-5 g/m2; 3-10 g/m2; 4-20 g/m2; 5-5 0g/m2
The integral emissivity increases monotonically with the particle concentration. But the value of ε has a limit, whose value depends substantially on the particle radius (see red curves in Fig. 2). Concentrations at which the limiting value of ε is reached are different for various radii. For instance, the layer with ρH > 20-30 g/m2 is quite thick at a = 0.5 μm, but the concentration over 50 g/m2 is necessary to reach this limit at a = 0.2 μm or 4 μm. The use of the concept of the limiting particle concentration, for which the additional particles do not result in any variation of the disperse layer emission, enables us to introduce the thickness of the effective radiating layer H*, which depends on ρ and a. To understand the physical sense of the limiting curve in Fig. 2, one should consider the spectral dependences of the particle optical properties. With the variation of the particle radius, the different regions of particle properties’ dependences on the diffraction parameters correspond to the wavelength of the blackbody radiation maximum,

Equation (2) is known as Wien’s displacement low, becauase it was developed independently by Wilhelm Wien (1894) before the publication of Plank’s emissive power law (Modest, 2003). For very small particles (a < 0.1 μm), the Rayleigh scattering takes place at λ = λm and the scattering coefficient is small in comparison to the absorption one. Therefore, the optically thick layer of such particles should be almost absolutely black. With increasing the particle radius, the maximum of transport scattering coefficient occurs near λm. For this reason, even the optically thick layer of such particles has a low integral emissivity. The role of scattering decreases with a further increase of the particle radius. As a result, the radiation of an optically thick layer increases with the further increase of the particle size. It should be noted that the limiting emissivity of the optically thick disperse system is not so sensitive to the particle transport albedo ωtr. This fact is quite obvious from the formula of the DP0 approximation (see the articles, “The simplest approximation of double spherical harmonics” and “Two-flux approximation”),
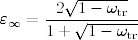
At ωtr << 1, this equation reduces to
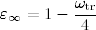
This means that comparatively low values of ε∞ for a cloud of molten alumina particles are explained by relatively high scattering of radiation by the particles. At low particle concentrations, the character of dependence ε(a) is determined by the absorption coefficient variation, since the role of scattering is negligible at small optical thickness of the particle layer (see blue curves in Fig. 2). The maximum of ratio Qa(x)/x at diffraction parameter x ≈ 6 leads to appearance of the corresponding maximum of ε(a) located near a = 1 μm at ρH > 10 g/m2.
The integral emissivity calculations for a monodisperse layer were performed also by assumption of isotropic scattering (see dashed-line curves in Fig. 2). This enables us to estimate the role of scattering anisotropy. At low optical thickness, the scattering does not influence the value of ε. If the layer has a large optical thickness, the anisotropy of scattering leads to a considerable increase in the integral radiation of the disperse system. In this case, the isotropic scattering model yields an integral emissivity about 25% lower than that in the exact solution.
The shape of a radiating volume (particle cloud) affects the emissivity when the particle cloud is not optically thick. This effect can be easily estimated by comparison of the analytical solutions to the following boundary-value problems (see the articles, “Differential approximations,” “Two-flux approximation, and “P1 approximation of spherical harmonics method”):


for n = 0 (plane-parallel layer), n = 1 (infinite cylinder), and n = 2 (sphere). These solutions can be written in the form (Dombrovsky and Baillis, 2010)

where
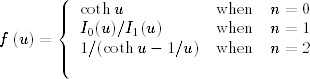
Here, I0 and I1 are the modified Bessel functions (Abramowitz and Stegun, 1965). In the limit of large optical thickness, we have f →1, and the above solutions are indistinguishable. In the opposite case of optically thin cloud, the limiting expressions for ελ are as follows:

A typical difference between integral emissivity of a plane-parallel layer and a cylindrical volume containing monodisperse alumina particles is shown in Fig. 3.
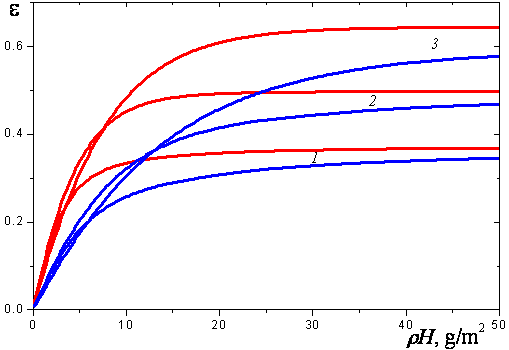
Figure 3. Comparison of integral emissivities of plane-parallel and cylindrical clouds of alumina particles at T = 3000 K: red curves--plane-parallel layer of thickness H; blue curves-cylindrical volume of diameter H; 1-a = 0.5 μm, 2-a = 1 μm, 3-a = 2 μm
The limiting value of integral hemispherical emissivity of optically thick volumes containing the particles of an aluminum oxide melt is often used in engineering calculations of radiative heat transfer in combustion chambers. This value depends on the particle temperature and size distribution. The dependences ε∞(a) for monodisperse particles are shown in Fig. 4. These computational results for particles of radius a > 0.5 μm can be approximated with high accuracy by the simple function
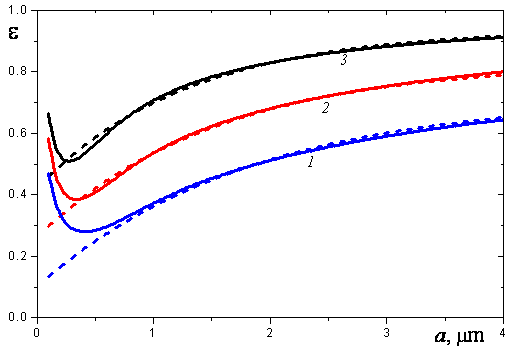
Figure 4. Integral hemispherical emissivity of an optically thick cloud containing monodisperse aluminum oxide particles: 1-T = 2500 K, 2-T = 3000 K, 3-T = 3500 K; solid lines--numerical solution, dashed lines--approximation (9)


where a is expressed in microns, R is expressed in degrees Kelvin.
The radiation calculations for polydisperse systems are much more complicated than those for monodisperse systems. Therefore, it is of interest to analyze a possibility of changing the polydisperse layer to a monodisperse one in the calculations. The problem of determination of the equivalent mean particle radius a*, for which the integral emissivity of the monodisperse layer at a = a* is approximately equal to that of the polydisperse one, has been considered by Dombrovsky (1976). It was assumed that an equivalent monodisperse layer has the same mass concentration of particles as that in the real medium. The calculations for large optical thickness showed the following value:

In the case of a two-parameter gamma-distribution (10) from the article “Radiative properties of polydisperse systems of independent particles,” Eq. (10) can be written as

By using Eqs. (9)-( 11), one can find the integral emissivity ε∞ with an error of <2% in the temperature range 2600 ≤ T ≤ 3600 K and typical size distributions (see Table 1). The emission spectrum of a polydisperse layer is also similar to the smoothed spectrum of the monodisperse with a = a* even for wide size distributions (Dombrovsky, 1976, 1996).
Table 1. Integral emissivity of an optically thick cloud of alumina particles
T, K | ε∞ | |||
| A = 2 μm-1, B = 2 | A = 3m-1, B = 2 | ||
| Complete calculation | Monodisperse approximation (numerical)/Eq. (9) | Complete calculation | Monodisperse approximation (numerical)/Eq. (9) |
2600 | 0.567 | 0.565/0.574 | 0.492 | 0.484/0.483 |
2800 | 0.634 | 0.636/0.638 | 0.557 | 0.552/0.552 |
3000 | 0.699 | 0.702/0.701 | 0.625 | 0.622/0.618 |
3200 | 0.760 | 0.764/0.761 | 0.690 | 0.691/0.683 |
3400 | 0.814 | 0.821/0.820 | 0.750 | 0.753/0.745 |
3600 | 0.861 | 0.869/0.876 | 0.806 | 0.811/0.806 |
For optically thin disperse systems containing molten alumina particles, one can use the value of a* = a43. But the monodisperse approach appears to be not applicable for intermediate optical thicknesses in the vicinity of the maximum of ε(a) (Dombrovsky, 1976).
A computational analysis of thermal radiation in typical combustion chambers showed that it is not important to take into account the absorption coefficient of gases by determination of the integral emissivity of the two-phase combustion products of aluminized solid propellants. For example, the calculated integral emissivity of an optically thick volume of combustion products at temperature 3460 K, pressure 5M Pa, mass fraction of condensed phase 0.34, and mole fractions of H2O-6.8%, CO2-0.6%, CO-25.9% is only 0.4% greater than the emissivity of the condensed phase without gases (Dombrovsky, 1996).
The combustion products of aluminized propellants may contain some optically inhomogeneous particles such as alumina particles with a core of aluminum, solidifying particles of alumina, alumina particles covered by a thin layer of soot, and even hollow solid alumina particles. The optical properties of these particles and their effect on the thermal radiation of combustion products have been analyzed in the book by Dombrovsky (1996) and are not reproduced here.
The qualitative results of the above computational analysis of thermal radiation of isothermal clouds of alumina particles may be of interest not only for heat transfer problems in solid rocket engines or in special power plants. These results are also applicable in general terms for disperse systems containing Mie particles of other weakly absorbing substances. The monodisperse approximation with appropriate choice of the equivalent particle size is also general enough. The latter will be illustrated for quite different disperse systems considered in another section of this chapter.
It should be noted that radiation heat transfer in a combustion chamber of a solid-propellant rocket engine is not a simple problem described by the only characteristic - the emissivity of an isothermal cloud of alumina particles. Particularly, the radiation flux to the burning surface of aluminized solid propellant as well as the radiation flux to the combustion chamber wall cannot be determined without in-depth analysis of conjugated combined heat transfer processes.
REFERENCES
Abramowitz, M. and Stegun, I. A. (eds.), Handbook of Mathematical Functions, Dover Publ., New York, 1965.
Brewster, M. Q., Radiation-stagnation flow model aluminized solid rocket motor internal insulator heat transfer, J. Thermophys. Heat Transfer, vol. 3, no. 2, pp. 132-139, 1989.
Der, J. J. and Nelson, D. A., Internal radiative heating from aluminum oxide particles in solid propellant rocket motors, AIAA Paper No. 1397, 1985.
Dombrovsky, L. A. and Ivenskikh, N. N., Radiation of homogeneous plane-parallel layer of spherical particles, High Temp., vol. 11, no. 4, pp. 818-822, 1973 (in Russian).
Dombrovsky, L. A., Radiation of plane-parallel layer of hollow spherical aluminum oxide particles, High Temp., vol. 12, no. 6, pp. 1316-1318, 1974 (in Russian).
Dombrovsky, L. A., Radiation of isothermal polydisperse layer, High Temp., vol. 14, no. 4, pp. 733-737, 1976.
Dombrovsky, L. A., Radiation Heat Transfer in Disperse Systems, Begell House, New York and Redding, CT, 1996.
Dombrovsky, L. A. and Baillis, D., Thermal Radiation in Disperse Systems: An Engineering Approach, Begell House New York and Redding, CT, 2010.
Kirshenbaum, A. D. and Cahill, J. A., The density of liquid aluminium oxide, J. Inorg. Nucl. Chem., vol. 14, no. 3-4, pp. 283-287, 1960.
Kuzmin, V. A., Maratkanova, E. I., and Dautov, E. A., Engineering method for disperse system thermal radiation calculations, Trans. High School, Aviat. Eng., vol. 1, pp. 74-78, 1989 (in Russian).
Lee, H., Scaled total hemispherical emittance of particle-gas layers, J. Thermophys. Heat Transfer, vol. 3, no. 1, pp. 61-67, 1989.
Mitin, B. S. and Nagibin, Yu. A., Density of liquid aluminum oxide, Russian J. Phys. Chem., vol. 44, no. 5, pp. 1325-1326, 1970 (in Russian).
Modest, M. F., Radiative heat transfer in a plane-layer mixture of non-gray particulates and molecular gases, J. Quant. Spectrosc. Radiat. Transfer, vol. 26, no. 6, pp. 523-533, 1981.
Modest, M. F., Radiative Heat Transfer, 2nd ed., Academic Press, New York, 2003.
Pearce, B. E., Radiative heat transfer within a solid-propellant rocket motor, J. Spacecraft Rockets, vol. 15, no. 2, pp. 125-128, 1978.
Popov, Yu. A., Calculation of infrared radiation of gas-particle medium, High Temp., vol. 22, no. 1, pp. 95-98, 1984 (in Russian).
Thynell, S. T., Radiation due to CO2 or H2O and particles in cylindrical media, J. Thermophys. Heat Transfer, vol. 4, no. 4, pp. 436-445, 1990.
Wien, W., Temperatur und Entropie der Strahlung, Annal. Phys., vol. 52, pp. 132-165, 1894.
References
- Abramowitz, M. and Stegun, I. A. (eds.), Handbook of Mathematical Functions, Dover Publ., New York, 1965.
- Brewster, M. Q., Radiation-stagnation flow model aluminized solid rocket motor internal insulator heat transfer, J. Thermophys. Heat Transfer, vol. 3, no. 2, pp. 132-139, 1989.
- Der, J. J. and Nelson, D. A., Internal radiative heating from aluminum oxide particles in solid propellant rocket motors, AIAA Paper No. 1397, 1985.
- Dombrovsky, L. A. and Ivenskikh, N. N., Radiation of homogeneous plane-parallel layer of spherical particles, High Temp., vol. 11, no. 4, pp. 818-822, 1973 (in Russian).
- Dombrovsky, L. A., Radiation of plane-parallel layer of hollow spherical aluminum oxide particles, High Temp., vol. 12, no. 6, pp. 1316-1318, 1974 (in Russian).
- Dombrovsky, L. A., Radiation of isothermal polydisperse layer, High Temp., vol. 14, no. 4, pp. 733-737, 1976.
- Dombrovsky, L. A., Radiation Heat Transfer in Disperse Systems, Begell House, New York and Redding, CT, 1996.
- Dombrovsky, L. A. and Baillis, D., Thermal Radiation in Disperse Systems: An Engineering Approach, Begell House New York and Redding, CT, 2010.
- Kirshenbaum, A. D. and Cahill, J. A., The density of liquid aluminium oxide, J. Inorg. Nucl. Chem., vol. 14, no. 3-4, pp. 283-287, 1960.
- Kuzmin, V. A., Maratkanova, E. I., and Dautov, E. A., Engineering method for disperse system thermal radiation calculations, Trans. High School, Aviat. Eng., vol. 1, pp. 74-78, 1989 (in Russian).
- Lee, H., Scaled total hemispherical emittance of particle-gas layers, J. Thermophys. Heat Transfer, vol. 3, no. 1, pp. 61-67, 1989.
- Mitin, B. S. and Nagibin, Yu. A., Density of liquid aluminum oxide, Russian J. Phys. Chem., vol. 44, no. 5, pp. 1325-1326, 1970 (in Russian).
- Modest, M. F., Radiative heat transfer in a plane-layer mixture of non-gray particulates and molecular gases, J. Quant. Spectrosc. Radiat. Transfer, vol. 26, no. 6, pp. 523-533, 1981.
- Modest, M. F., Radiative Heat Transfer, 2nd ed., Academic Press, New York, 2003.
- Pearce, B. E., Radiative heat transfer within a solid-propellant rocket motor, J. Spacecraft Rockets, vol. 15, no. 2, pp. 125-128, 1978.
- Popov, Yu. A., Calculation of infrared radiation of gas-particle medium, High Temp., vol. 22, no. 1, pp. 95-98, 1984 (in Russian).
- Thynell, S. T., Radiation due to CO2 or H2O and particles in cylindrical media, J. Thermophys. Heat Transfer, vol. 4, no. 4, pp. 436-445, 1990.
- Wien, W., Temperatur und Entropie der Strahlung, Annal. Phys., vol. 52, pp. 132-165, 1894.