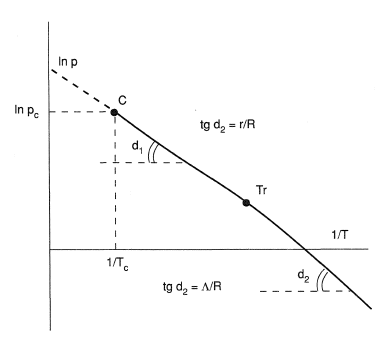
Any substance in a solid or liquid phase at any temperature is characterized by an equilibrium vapor pressure. As a first approximation this vapor pressure is a function only of the temperature and is defined by the Clapeyron-Clausius equation. The equilibrium pressure above a solid becomes zero at temperature 0 K and increases monotonically up to the triple point. The equilibrium vapor pressure for the liquid increases from the triple point until the critical point.
For most substances the triple point pressure is lower than atmospheric pressure. These substances can exist at atmospheric pressure as liquids. If the triple point pressure is higher than the atmospheric pressure, the liquid phase does not exist at atmospheric pressure and the solid substance directly evaporates (sublimates) (Figure 1a and 1b).
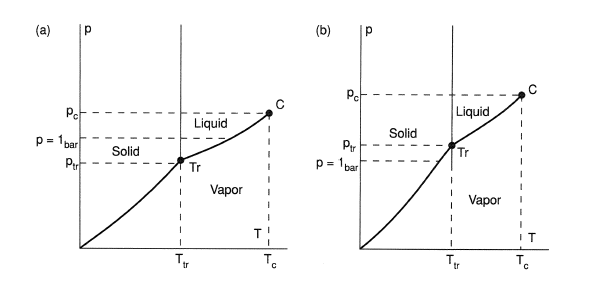
Figure 1. Vapor pressure as a function of temperature, (a) case where triple point lies below 1 bar (atmospheric pressure), (b) case where triple point lies above 1 bar (solid sublimates).
For most pure substances the equilibrium vapor pressures are defined experimentally and tabulated.
Usually as a first approximation the equilibrium vapor pressure ps for a liquid at any temperature T can be calculated if the normal boiling temperature (Tn.b.) (the temperature at which the equilibrium vapor pressure is equal to 1 phys.atm = 0.1033MPa) as well as the heat of evaporation r at this temperature are known:

This equation is plotted in Figure 2. It is a segment of straight line between the critical point K and triple point Tr, which has a slope r/R.
The equilibrium vapor pressure for a solid substance can be described by a similar equation:

here the subscript tr refers to the tripple point; Λ is the heat of sublimation.
At the triple point

where L is the heat of fusion.
In the case where condensed (liquid or solid) substance is not only under its equilibrium vapor pressure but sustains an additional positive or negative pressure, the equilibrium pressure itself becomes a function of this additional pressure.
The influence of the additional pressure can be accounted for by taking advantage of the thermodynamic phase equilibrium condition saying that the specific Gibbs functions of phase being in equilibrium have to be equal:
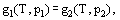
where the subscripts 1 and 2 refer to the respective phases.
If, at constant temperature, the pressure upon the phase 1 (condensed phase) will be changed, the equation has to be valid:

As for as the derivative
 , one can derive from (5):
, one can derive from (5):
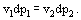
This equation is known as the Pointing equation.
At moderate pressures v1 can be regarded as independent from the pressure; whereas v2 can be expressed via the perfect gas equation of state: v2 = RT/p2.
With these assumptions the Pointing equation will be expressed as

which after integration gives

where p0 is the equilibrium vapor pressure at the temperature T, without any additional pressure, i.e., when the pressures in both phases are equal.
Equation (7) can be rearranged:
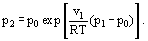
This equation is in particular of interest when the equilibrium vapor pressure above a curved liquid surface is defined. In this case, according to Laplace equation, a spherical liquid surface sustains an additional pressure
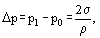
where σ is the surface tension; ρ is the radius curvature of the surface. In this equation, if the liquid surface is convex, ρ is positive, for a concave surface ρ is negative.