Convective nucleate boiling on a tube differs considerably from that on a flat plate. In the latter case, bubbles are formed at scattered nucleation sites and depart taking part of the superheated boundary layer with them and causing an in-rash of fresh liquid to the surface. The convective effects are often characterized using the bubble diameter at departure.
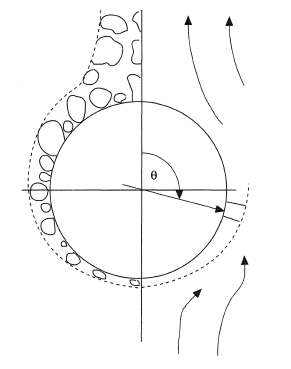
In the case of a horizontal tube, observation shows that nucleation occurs primarily at the underside of the tube and that the bubbles then slide parallel to the surface to a point near the top before they depart. Thus a bubble-layer is formed around the tube as shown in Figure 1 and analysis [Cornwell and Einarsson (1990)] of a radial control volume shows a voidage varying from virtually zero at the base to around 0.5 at the sides with a corresponding rapid increase in velocity. There is a considerable peripheral variation of heat transfer coefficient on the tube. (This is largely smoothed out in most experiments by the peripheral conduction in the tube.)
Typical test results for a 27 mm diameter tube are shown in Figure 2 where U is the vertical liquid velocity, with pool boiling therefore at U = 0. The value of α increases from the base to the sides in direct opposition to that for single-phase flow where it drops. This increase is caused by the increase in bubble layer velocity from the base and by the additional latent heat transport from the thin layers formed under the bubbles as they slide around the surface. This latter mechanism becomes more important as the liquid velocity increases and accounts for the bulge which develops at higher velocities at the sides.
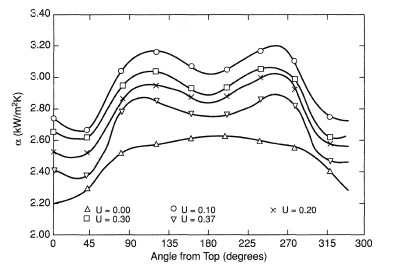
Figure 2. Peripheral variation of heat transfer coefficient at various approach velocities (in m/s) for boiling R113 at 1 atmosphere at
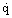 = 25 kW/m2K.
= 25 kW/m2K.
Estimation of boiling heat transfer coefficients for tubes have generally relied on pool boiling correlations developed from flat plate nucleation concepts (although it is known that tubes can yield higher values). This may be a reasonable approach at high heat fluxes (q > 0.5 qcrit) where the boiling is vigorous but at lower fluxes where most industrial systems operate the difference can be considerable. The following general correlation [Cornwell and Houston (1994)] is based on the convective nature of tube boiling with Reynolds number, Reb, representing the vapor production rate into the bubbly layer from a tube, diameter D,
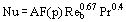
Here
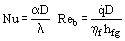
The pressure dependence is the same as that for pool boiling [from Mostinski (1963)]

where pr is the critical pressure ratio

The constant A is fluid dependent and the best fit for the available world data is given by
 This correlation indicated by the line in Figure 3 applies to pool boiling (no imposed flow) and on tube diameters in the range 8–50 mm, with a natural or "as-machined" surface and normal industrial fluids (not liquid metals or cryogenic fluids). The considerable scatter is to be expected for boiling correlations which cover a wide range of fluids, surfaces and pressures, particularly where data extending back over 50 years are included.
This correlation indicated by the line in Figure 3 applies to pool boiling (no imposed flow) and on tube diameters in the range 8–50 mm, with a natural or "as-machined" surface and normal industrial fluids (not liquid metals or cryogenic fluids). The considerable scatter is to be expected for boiling correlations which cover a wide range of fluids, surfaces and pressures, particularly where data extending back over 50 years are included.
Boiling on a column of tubes has been shown to yield progressively enhanced heat transfer from the lowest tube upwards due to the liquid velocity and presence of bubbles in the flow. The effect of the liquid flow is evident from Figure 2, but the influence of the vapor is complicated by the form of flow which may range from bubbly to separated in nature. Figure 4 shows the influence of variation in the dryness fraction λ, κ, of the approaching flow for the same tube used for Figure 2 (at a constant flow rate equivalent to u = 0.1 m/s). Most industrial equipment with boiling outside tubes operates at low quality where the strong enhancement of heat transfer at the sides of the tubes is important.

Figure 4. Peripheral variation of heat transfer coefficient (under similar conditions to those in Figure 2) with dryness fraction, Cornwell (1990).
The complex nature of the flow in bundles is well illustrated in Figure 5 where there is high velocity bubbly flow upwards between the tubes and relatively motionless liquid in the horizontal gaps. Tubes in the upper part of a bundle usually experience a high-voidage pseudo-annular flow and the space above may be filled with foam which may result in liquid carry-over problems.
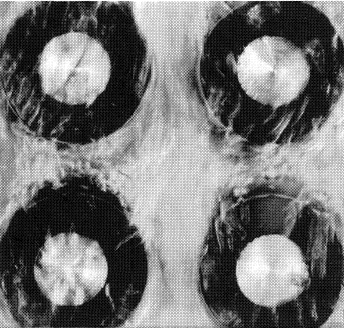
Since 1829, when George Stephenson first boiled water on the outside of a tube bundle in his "Rocket" locomotive, boiling on the shell-side of bundles has been a common process in the power and process industries. Fire-tube and waste heat boilers which raise steam from hot gases generally have well spaced, large diameter tubes and the primary resistance to heat transfer is on the gas side. Natural circulation reboilers and once-through evaporators as used in process industries have more compact bundles as shown in Figure 6 (see also Evaporators; Reboilers.) The liquid forced convection or condensation on the tube-side can result in more equal matching of the heat transfer resistances on the tube and shell sides.
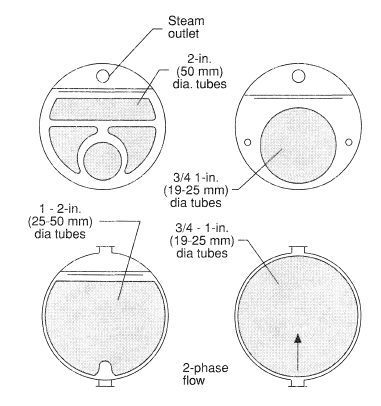
Figure 6. Sections through shell and tube boilers; clockwise from top left, fire-tube boiler, kettle reboiler, full-bundle evaporator, waste heat boiler.
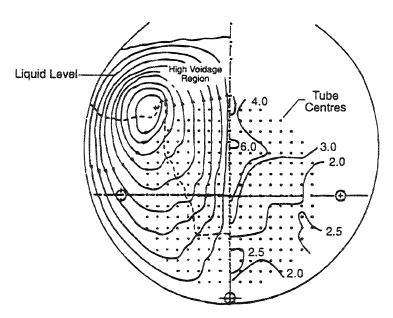
Of these arrangements, the close-packed bundle in a liquid reservoir, as found, for example, in shell-side refrigeration chillers and in distillation reboilers, is the most difficult to analyze. The general flow of the liquid and entrained vapor and the resultant variation of heat transfer coefficients within the bundle are typically as shown in Figure 7. Analytic methods used until the 1960s were excessively conservative and led to overdesigned equipment. Later approaches were generally based on the pool boiling heat flux on a single tube of the type used in the bundle. However, Figure 8 shows that the mean heat flux for the bundle is greater than that for an isolated tube, although the critical heat flux (at which the surface is blanketed by vapor) is lower.
The large range of variables involved in the complex fluid flow and heat flow processes in boiling outside bundles make it unlikely that the gap between the understanding of the local mechanisms at the tube and the estimation of the overall bundle heat transfer coefficient, αb, can be bridged. However, knowledge of the mechanisms has successfully highlighted the most viable approaches for developing design correlations.
Palen (1983) essentially recommends adaption of the single-tube nucleate boiling heat transfer coefficient αnb by a bundle boiling factor Fb, a mixture correction factor Fc and natural convection αnb in the form

Factor Fb may be calculated, but when data is not available a conservative value of 1.5 is recommended. Fc is unity for pure fluids, but less for mixtures and αnc is around 0.25kW/m2K (small compared to αnb).
More recent work [by Fujita et al. (1986), Jensen (1989), Cornwell et al. (1992), for example)] has shown that both the pressure drop and the heat transfer through the bundle can be estimated using two-phase flow theory for in-tube flow, suitably modified for the different geometry and the different flow regimes. Under normal conditions bundles operate in the bubbly flow regime with the upper tubes in a pseudo-annular flow. Calculation of the pressure drop is needed to determine circulation rates and readers are referred to Schrage et al. (1988) for voidage and two-phase friction multiplier data for vertical crossflow over horizontal bundles.
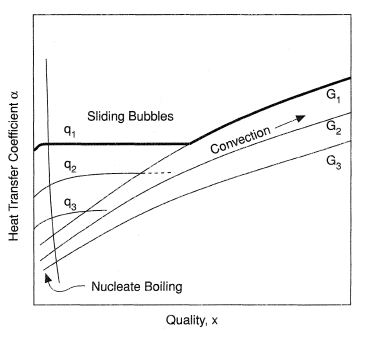
Variation of the heat transfer coefficient up the bundle with the dryness fraction x (typically from x = 0 to 0.2 in a submerged bundle) is shown in Figure 9. Correlations for in-tube evaporation such as Chen (1966) which sum the nonconvective part (at low x) and the convective part have been successfully adapted for this geometry. Alternatively, bearing in mind the bubbly-flow sliding bubble mechanism at low x and the very different forced convective evaporation mechanism at higher x, appropriate relationships may be applied separately to the two regimes so that for each tube (suffix t)

or

whichever is the larger. Here αnb is as before and F is the Chen two-phase convective flow factor which is a function of x (see section on Forced Convective Boiling). The liquid-only crossflow heat transfer coefficient αio may be found from Žukauskas and Ziudzda (1985) or ESDU (1973) (See also Tube Banks, Single-Phase Heat Transfer in):

This approach will lead to conservative values because, as explained earlier, the single tube value αt is likely to be more than αnb The mean bundle value αb may be estimated by integration over the x range or averaging the αt values for the bundle.
Process intensification has led to increasing use of plate and narrow channel geometries of heat exchangers in place of shell and tube arrangements. Where manufacturing processes and fouling rates allow, the use of smaller diameter tubes and lower pitch/diameter ratios can lead to compact and effective evaporator bundles [Cornwell et al. (1992)]. Enhancement of heat transfer on the outer, boiling side of the tube using porous or grooved surfaces to increase the nucleation site density or by using low-fin tubes can increase αb for a tube by up to 10 times (see Augmentation of Heat Transfer, Two-Phase Systems.) Use of these tubes lead to an overall increase in bundle performance of typically around 2 owing to the predominance of convective boiling rather than nucleate boiling and the resistance of the inner tube side [see review by Thome (1989)].
Mixture boiling on bundles, as for boiling generally, leads to lower heat transfer rates owing to the local composition gradients. The critical (maximum) heat flux for a bundle is generally around 0.5 to 1 times the single tube value and Leroux and Jensen (1992) have shown that it is highly mass flux dependent. The influence of mechanical features, corrosion, fouling, cleaning and maintenance of horizontal-tube boilers and samples of design calculations are covered by Smith (1986).
REFERENCES
Chen, J. (1966) A correlation for boiling heat transfer to saturated fluids in convective flow, I & EC Proc. Des. Dev. 5, 322–329.
Cornwell, K. (1990) The role of sliding bubbles in boiling on tube bundles, Heat Transfer 1990, 9th Int. Heat Transfer Conf. Proc., 1, 455–460, Hemisphere.
Cornwell, K., Dewar, R. G., and Ritchie, J. M. (1992) A new approach to the determination of boiling heat transfer coefficients outside tube bundles, heat transfer, I Chem E, 3rd UK National Heat Transfer Conference 1, 51–64.
Cornwell, K., Duffin, N. W. and Schuller, R. B. (1980) An Experimental Study of the Effects of Fluid Flow on Boiling Within a Kettle Reboiler Tube Bundle, ASME Paper 80-HT-45.
Cornwell, K. and Einarsson, J. G. (1990) The influence of fluid flow on nucleate boiling from a tube, Exp. Heat Transfer, 3, 101–116.
Cornwell, K. and Houston, S. D. (1994) Nucleate pool boiling on horizontal tubes: a convection-based correlation, Int. J. Heat Mass Trans., 37, 303–309. DOI: 10.1016/0017-9310(94)90031-0
ESDU (1973) Convective Heat Transfer During Crossflow of Fluids Over Plain Tube Banks, Item No. 73071, ESDU, London.
Fujita, Y., Ohta, H., Hidaka, S. and Niskikawa, K. (1986) Nucleate boiling on horizontal tubes in bundles, 8th International Heat Transfer Conference, San Francisco, 5, 2131–2136.
Jensen, M. K. (1989) Advances in shellside boiling and two-phase flow, ASME, HTD, 108, 1–11.
Kern, D. Q. (1950) Process Heat Transfer, McGraw Hill, New York.
Leroux, K. M. and Jensen, M. K. (1992) Critical heat flux in horizontal tube bundles in vertical crossflow of R113, J. Heat Trans., 114, 179–185.
Mostinski, I. L. (1963) Calculation of heat transfer and critical heat flux in boiling liquids based on the law of corresponding states, Teploenergetika, 10, 66–71.
Palen, J. W. (1983) Shell and tube reboilers, Heat Exchanger Design Handbook, Hemisphere, New York.
Schrage, D. S., Hsu, J.–T., and Jensen, M. K. (1988) Two-phase pressure drop in vertical crossflow across a horizontal tube bundle, AICHEJ, 34, 107–115.
Smith, R. A. (1986) Vaporisers, Longman, Harlow, UK.
Thome, J. R. (1989) Enhanced Boiling Heat Transfer, Hemisphere, NY.
Žukauskas, A. and Ziugzda (1985) Heat Transfer in a Cylinder in Crossflow, Hemisphere, NY.
References
- Chen, J. (1966) A correlation for boiling heat transfer to saturated fluids in convective flow, I & EC Proc. Des. Dev. 5, 322–329.
- Cornwell, K. (1990) The role of sliding bubbles in boiling on tube bundles, Heat Transfer 1990, 9th Int. Heat Transfer Conf. Proc., 1, 455–460, Hemisphere.
- Cornwell, K., Dewar, R. G., and Ritchie, J. M. (1992) A new approach to the determination of boiling heat transfer coefficients outside tube bundles, heat transfer, I Chem E, 3rd UK National Heat Transfer Conference 1, 51–64.
- Cornwell, K., Duffin, N. W. and Schuller, R. B. (1980) An Experimental Study of the Effects of Fluid Flow on Boiling Within a Kettle Reboiler Tube Bundle, ASME Paper 80-HT-45.
- Cornwell, K. and Einarsson, J. G. (1990) The influence of fluid flow on nucleate boiling from a tube, Exp. Heat Transfer, 3, 101–116. DOI: 10.1080/08916159008946380
- Cornwell, K. and Houston, S. D. (1994) Nucleate pool boiling on horizontal tubes: a convection-based correlation, Int. J. Heat Mass Trans., 37, 303–309. DOI: 10.1016/0017-9310(94)90031-0
- ESDU (1973) Convective Heat Transfer During Crossflow of Fluids Over Plain Tube Banks, Item No. 73071, ESDU, London.
- Fujita, Y., Ohta, H., Hidaka, S. and Niskikawa, K. (1986) Nucleate boiling on horizontal tubes in bundles, 8th International Heat Transfer Conference, San Francisco, 5, 2131–2136.
- Jensen, M. K. (1989) Advances in shellside boiling and two-phase flow, ASME, HTD, 108, 1–11.
- Kern, D. Q. (1950) Process Heat Transfer, McGraw Hill, New York.
- Leroux, K. M. and Jensen, M. K. (1992) Critical heat flux in horizontal tube bundles in vertical crossflow of R113, J. Heat Trans., 114, 179–185. DOI: 10.1115/1.2911244
- Mostinski, I. L. (1963) Calculation of heat transfer and critical heat flux in boiling liquids based on the law of corresponding states, Teploenergetika, 10, 66–71.
- Palen, J. W. (1983) Shell and tube reboilers, Heat Exchanger Design Handbook, Hemisphere, New York.
- Schrage, D. S., Hsu, J.–T., and Jensen, M. K. (1988) Two-phase pressure drop in vertical crossflow across a horizontal tube bundle, AICHEJ, 34, 107–115. DOI: 10.1002/aic.690340112
- Smith, R. A. (1986) Vaporisers, Longman, Harlow, UK.
- Thome, J. R. (1989) Enhanced Boiling Heat Transfer, Hemisphere, NY.
- Žukauskas, A. and Ziugzda (1985) Heat Transfer in a Cylinder in Crossflow, Hemisphere, NY.