The principal difference in the behavior of a fluid as its temperature is raised above the critical temperature is evident from the pressure-volume diagram shown in Figure 1. Below the critical temperature Tc the variation of pressure p and volume v along an isotherm shows discontinuities where the isotherm intersects the saturation line. Phase change occurs at the saturation line, and the horizontal constant pressure segment of the isotherm represents the presence of vapor and liquid in varying proportions. The critical temperature isotherm has zero slope at one point, the pressure there being the critical pressure, pc. Above the critical temperature, isotherms show no discontinuity and from a macroscopic standpoint there is a continuous variation from a liquid-like fluid to a gas-like fluid.
Since the pressure variation across most thermal boundary layers is negligible, it is the variation of properties along an isobar that is important. The variation of specific volume v, specific heat cp, absolute viscosity η, thermal conductivity λ and specific enthalpy h for water at pressure of 245 bar is shown in Figure 2 The temperature at which the specific heat reaches a peak is known as the pseudocritical temperature, Tpc. As the pressure is increased this temperature increases, the maximum value of the specific heat falls, and the variation of the other properties becomes less severe.
Convective heat transfer near the critical point is characterized by properties having rapid variation with temperature. As a consequence, the flow and heat transfer processes are linked. Moreover, the equation describing the temperature distribution in the fluid is essentially nonlinear, so that the proportionality between heat flux and temperature difference no longer exists; in these circumstances heat transfer coefficient is a parameter of doubtful utility which can take widely differing values depending on the conditions.
Forced convection heat transfer measurements in pipes to fluids at supercritical pressure have been made using a wide range of fluids: water, carbon dioxide, nitrogen, hydrogen and helium are examples. By far the most extensive collections of data are for water and carbon dioxide, and fortunately the accuracy of physical property data for these fluids is good. The incentive for work on water has been its use in supercritical pressure "boilers" for power stations, particularly in the U.S.A. and the U.S.S.R. For the experimentalist carbon dioxide is an easier fluid to handle because of its lower critical temperature and pressure (31°C and 73.8 bar, compared with 370°C and 221 bar for water).
Several reviews of supercritical pressure forced convection have been written: for example, Petukhov (1970), Hall (1971) and Hall, Jackson (1978). This account is largely based on the last of these.
At very low heat fluxes, and therefore with small temperature variations in the fluid, one approaches the case of constant properties. Their actual value in this small temperature range will, of course, depend upon where the temperature lies in relation to the critical temperature. Thus, while the physical properties may remain almost uniform throughout the fluid, they may be made to traverse a wide range of values by adjusting the bulk mean temperature of the fluid in the limiting case of a very small heat flux. There is no reason why constant property equations should not work. Consider the well-known expression

where Nu is the Nusselt Number (= αD/λ), Re is the Reynolds Number (=
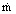 D/η), and Pr is the Prandtl Number (=ηcp/λ), in which α is Heat Transfer Coefficient and
D/η), and Pr is the Prandtl Number (=ηcp/λ), in which α is Heat Transfer Coefficient and
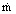 is mass flow rate per unit area.
is mass flow rate per unit area.
From this it follows that

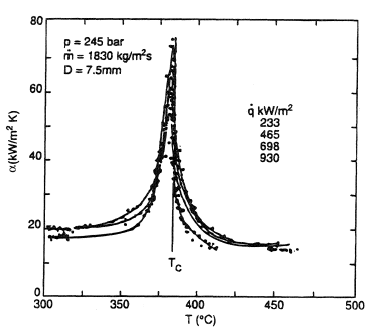
Noting that the variations with temperature, of the thermal conductivity λ, and the viscosity η are rather similar in form (Figure 2), one would not expect a major effect on the heat transfer coefficient on this account. The specific heat, on the other hand, becomes very large in the vicinity of the pseudocritical temperature, and one might expect the heat transfer coefficient to behave in a similar manner. This, in fact, happens, as is well illustrated by the data of Yamagata et al. for water (Figure 3). It will be noted that as the heat flux
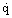 increases the magnitude of the peak in the heat transfer coefficient decreases. This is because the region of fluid at high Prandtl Number contracts as the heat flux, and hence the temperature gradient, increases.
increases the magnitude of the peak in the heat transfer coefficient decreases. This is because the region of fluid at high Prandtl Number contracts as the heat flux, and hence the temperature gradient, increases.
Heat flux is not the sole determinant of the effects, which are about to be described. However, for a given size and orientation of pipe and a given flow rate, the effects are very largely determined by heat flux. Under some conditions the orientation of the pipe becomes important, and very different results are obtained depending upon whether the pipe is horizontal or vertical, and whether in the latter case the flow is upwards or downwards.
In cases where orientation is not important the deterioration in heat transfer coefficient with heat flux that was evident in Figure 3 becomes more marked both with decreasing mass velocity and increase of heat flux. Figure 4 shows the water data of Vikhrev et al. for a constant mass flow and three levels of heat flux, the highest of which results in virtually no enhancement of a as the bulk temperature traverses the pseudocritical temperature.
Turning to data in which the orientation of the pipe is important, we find that under some conditions of pipe diameter, mass flow and heat flux, heat transfer to a fluid is much better in a vertical pipe when the flow is in the downward rather than upward. When it was first observed, this behavior was difficult to reconcile with the currently held view that forced and free convection reinforced each other when they acted in the same direction. An example of this behavior is shown in Figure 5 where the data of Jackson and Evans-Lutterudt for carbon dioxide at two different heat fluxes are shown for both upward and downward flow. It will be seen that there is a rapid deterioration in heat transfer following a relatively small increase in heat flux with upward flow but not with downward flow.
An interesting comparison between carbon dioxide data that is unaffected by the direction of flow and with data that is so affected is shown in Figure 6. All three sets of data have been selected so that, in the absence of any gravitational effect, they would be expected to yield similar distributions of wall temperature against bulk enthalpy. In the case of one set of data (due to Shiralkar and Griffith), no difference between upward and downward flow was found, whereas the other two sets (due to Jackson and Evans-Lutterudt and Bourke et al.) showed such a difference. The sharp temperature peaks appear to be characteristic of upward heated flows in which gravitation is important. Note that, following these peaks, heat transfer is better than it would have been in the absence of gravitational effects, and also that in downward flow there is substantially improved heat transfer with no wall temperature peaks.
The examples of the effect of orientation of the pipe that have been quoted above confirm the importance of interactions between forced and free convection. The sharp peaks in the wall temperature that occur with upward heated flows were first attributed to "pseudofilm boiling". The true nature of the phenomenon was revealed when results for both upward and downward flow became available, and it is now possible to say with some confidence whether it is likely to occur in given circumstances. The exclusion of data affected by buoyancy is clearly necessary preliminary before any attempt can be made to correlate data for pure forced convection.
An explanation of the mechanism by which buoyancy affects heat transfer has been proposed by Hall and Jackson (1969). The dominant factor is the modification of the shear stress distribution across the pipe, with a consequential change in turbulence production.
It can be shown that a criterion for negligible buoyancy effects is

where
 is the Grashof Number (= g(ρb −
is the Grashof Number (= g(ρb −
 )D3/
)D3/
 ), in which
), in which
 is the integrated mean density and the subscript b indicates physical properties evaluated at the local bulk temperature.
is the integrated mean density and the subscript b indicates physical properties evaluated at the local bulk temperature.
The application of the above criterion is made difficult by the fact that evaluation of the Grashof Number requires that the wall temperature Tw is known, so that in applications where the wall heat flux is specified a correlation describing forced convection heat transfer (with negligible buoyancy effects) must be used in conjunction with the criterion.
The enhancement of heat transfer coefficient at small temperature differences when the bulk temperature is close to the pseudocritical temperature has already been noted and attributed to the large value of cp in this region. As the temperature difference is increased, the proportion of the flow experiencing this high specific heat shrinks, and the heat transfer coefficient is reduced. If we take the temperature difference as the main factor affecting enhancement of the heat transfer coefficient (for a given fluid and bulk temperature) then it follows that the effect should be characterized by a quantity such as
 . Attempts have been made to express the ratio of the heat transfer coefficient to that for constant properties in terms of the quantity
. Attempts have been made to express the ratio of the heat transfer coefficient to that for constant properties in terms of the quantity
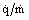 ; typical of these are the generalized curves of Lokshin for water at 250 bar (Figure 7). It is seen that above a value of
; typical of these are the generalized curves of Lokshin for water at 250 bar (Figure 7). It is seen that above a value of
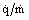 ≈ 0.7 no enhancement occurs and there is a monotonic decrease in a as the fluid bulk temperature traverses the pseudocritical temperature.
≈ 0.7 no enhancement occurs and there is a monotonic decrease in a as the fluid bulk temperature traverses the pseudocritical temperature.
Many attempts have been made to correlate forced convection data in terms of conventional dimensionless groups with modifications to allow for the effect of physical property variation. Jackson et al. (1975) have made a study of virtually all known correlations and have compared their performance when tested against forced convection data for water and for carbon dioxide. The fact that they were able to exclude data that may have been affected by buoyancy constituted an important advance over earlier attempts to correlate forced convection data. They found that by far the most effective correlation was that published in 1965 by Krasnoschekov and Protopopov (1966). This utilizes the Petukhov-Kirrillov equation for constant properties forced convection and accounts for property variation by additional terms involving wall to bulk density ratio and integrated to bulk specific heat ratio, each raised to suitable powers. It correlated 80% of the data points to within ± 15% and 91% to within ± 20%. Because the Petukhov-Kirrillov equation was rather cumbersome to use Jackson and Fewster also tried the following simpler version in which a Dittus-Boelter form of constant properties forced convection equation is used instead:

where suffix w refers to conditions at the wail,

and




In this form the equation correlated 77% of the data points to ± 15% and 90% to within ± 20%. Approximately 2000 data points were tested against the correlation.
This topic has already received some discussion and a criterion for the onset of buoyancy effects has been given. Also the tendency towards the sudden occurrence of localized peaking of the wall temperature in upward flow with increase of heat flux has been noted. In view of this instability it is not surprising that the magnitude of the subsequent increase in wall temperature (for conditions of specified heat flux) has proved difficult to predict. For a detailed picture of the influences of buoyancy on heat transfer to fluids in vertical pipes, including fluids at supercritical pressure, see Jackson and Hall (1980).
For a downward heated flow there is a continuous enhancement in heat transfer as buoyancy becomes relatively stronger. This behavior has been found with many fluids at supercritical pressure and also with other fluids. Not only is the heat transfer improved, but wall temperatures are less sensitive to heat flux.
As might be expected, buoyancy in uniformly heated horizontal pipes causes a progressive increase in the temperature of the upper surface relative to the lower surface of the pipe. This is undoubtedly due in part to a stratification of the flow, the hotter and less dense fluid occupying the upper part of the pipe; there may also be an effect due to the damping effect of the stabilizing density gradient on turbulence near the upper surface of the pipe. At the lower surface heat transfer is frequently better than for forced convection alone, suggesting that there may be some amplification of turbulence by the destabilizing density gradient in this region. For a detailed review of the effects of buoyancy on heat transfer to fluids flowing in horizontal tubes, including fluids at supercritical pressure, see Jackson (1983).
A considerable number of measurements on horizontal pipes have been made using fluids at supercritical pressure. A typical set of data presented by Belyakov et al. is reproduced in Figure 8. The deterioration of the upper surface occurs progressively along the pipe and does not show the sharp peaks that are obtained with upward flow.
Free convection in supercritical pressure fluids has received a good deal less attention than has forced convection, presumably because there have been fewer pressing industrial applications. The situation was reviewed by Hall (1971), and little further data have been reported since that time.
The general picture is one of enhancement of heat transfer at low heat fluxes with surface and fluid temperature spanning the pseudocritical temperature. As with forced convection, the enhancement is greatest when the bulk temperature is close to the critical temperature, but there is no evidence of the impairment of heat transfer that is found at high heat fluxes with forced convection.
Nucleation at a boiling site of a given size becomes easier as the pressure of a boiling liquid increases. The decrease of surface tension means that a smaller difference between vapor and liquid pressure is required in order to make a nucleus grow; moreover, a given pressure difference can be achieved with a smaller superheat as the pressure level increases. For a given superheat, therefore, it will be possible to activate smaller nuclei at higher pressures.
In addition to this effect, there is the possibility of spontaneous nucleation occurring as a result of thermal fluctuations in a superheated liquid at a surface as p/pc approaches unity. Indeed, it may be that the very "quiet" transition to film boiling that occurs at high pressure may be a consequence of spontaneous nucleation.
The effect of pressure on nucleate boiling is well established: as the pressure is raised towards the critical pressure the heat transfer coefficient increases, and the limiting heat flux for transition from nucleate to film boiling first increases, reaches a maximum at a value of p/pc of about 0.35, and then decreases.
Pool boiling experiments at high pressures show very clearly how the range of conditions under which nucleate boiling occurs is contracted by transition to film boiling.
Following transition to film boiling at pressures close to the critical value, a highly regular flow of vapor from the heated surface is observed. At p/pc ≈ 0.9 uniformly spaced columns of bubbles are observed to rise from a heated wire. As the critical pressure is approached these columns change into "tubes" of vapor, again with very regular spacing, and finally change further into what appears to be a sheet of vapor rising from the wire.
As indicated earlier, the general picture of supercritical pressure forced convection has become comparatively clear. In contrast, very few detailed investigations have been made at high subcritical pressures.
Figure 9 shows data for water flowing upwards in a 20-mm diameter pipe for pressures extending from subcritical to slightly supercritical, taken from the work of Herkenrath et al. It is of interest to compare the subcritical curves, each of which involves a local heat transfer crisis, with the curve for supercritical pressure, which does not. Note that the conditions are such that buoyancy induced temperature peaks would not be expected in the case of the supercritical data.
It will be seen from Figure 9 that as the pressure is increased the position of the heat transfer crisis shifts towards the region of lower quality; the magnitude of the wall temperature step at first decreases, then increases and finally decreases as the critical pressure is approached. Furthermore, the shape changes from a sharp to a more gradual increase in wall temperature. Some data obtained by the present author and co-workers using carbon dioxide at a reduced pressure, p/pc = 0.99, for both upward and downward flow showed an increase in wall temperature following transition which was rather gradual (the curve for p = 215 bar in Figure 9) and that in upward flow peaks develop due to buoyancy influence as they do at supercritical pressure. It was also apparent that at high subcritical pressures downward flow was advantageous, just as at supercritical pressures: transition occurred later in downward flow and the consequences were less severe. Experiments with carbon dioxide at lower pressure show a sharp transition rather similar to those illustrated in Figure 9.
The beneficial consequences of buoyancy in downward flow do not appear to persist as the pressure is dropped further, where the above mentioned trend appears to be reversed.
REFERENCES
Hall, W. B. (1971) Heat transfer near the critical points, Advances in Heat Transfer, Vol. 6, Academic Press, New York.
Hall, W. B. and Jackson, J. D. (1969) Laminarisation of a turbulent pipe flow by buoyancy forces, ASME Paper No. 69-HT-55.
Hall, W. B. and Jackson, J. D. (1978) Heat transfer near the critical point, Keynote Lecture, Sixth International Heat Transfer Conference, Toronto, Canada.
Jackson, J. D. (1983) Effects of Buoyancy on Heat Transfer to Fluids Flowing in Horizontal Heat Tubes, Proc. H.T.F.S. Research Symposium, University of Bath, Paper RS 471, 97-115.
Jackson, J. D., Hall, W. B., Fewster, J., Watson, A., and Watts, M. J. (1975) Heat Transfer to Supercritical Pressure Fluids, H.T.F.S. Design Report No. 34, Part 1—Summary of design recommendations and equations, Part 2—Critical reviews with design recommendations, AERE-R8157 and R8158, U.K.A.E.A., AERE, Harwell.
Jackson, J. D. and Hall, W. B. (1980) Influences of buoyancy on heat transfer to fluids flowing in vertical tubes under turbulent conditions, 563-611, Turbulent Forced Convection in Channels and Rod Bundles, published by Hemisphere Publishing Corporation, USA (S. Kakacs and D.B. Spalding, Eds.)
Krasnoschekov, E. A. and Protopopov, V. S. (1966) Experimental study of heat exchange in carbon dioxide in the supercritical range at high temperature drops, Teplofizika Vysokikh Temperatur, Vol. 4, No. 3.
Petukhov, B. S. (1970) Heat transfer and friction in turbulent pipe flow with variable physical properties, Advances in Heat Transfer, Vol. 6, Academic Press, New York.
References
- Hall, W. B. (1971) Heat transfer near the critical points, Advances in Heat Transfer, Vol. 6, Academic Press, New York.
- Hall, W. B. and Jackson, J. D. (1969) Laminarisation of a turbulent pipe flow by buoyancy forces, ASME Paper No. 69-HT-55.
- Hall, W. B. and Jackson, J. D. (1978) Heat transfer near the critical point, Keynote Lecture, Sixth International Heat Transfer Conference, Toronto, Canada.
- Jackson, J. D. (1983) Effects of Buoyancy on Heat Transfer to Fluids Flowing in Horizontal Heat Tubes, Proc. H.T.F.S. Research Symposium, University of Bath, Paper RS 471, 97-115.
- Jackson, J. D., Hall, W. B., Fewster, J., Watson, A., and Watts, M. J. (1975) Heat Transfer to Supercritical Pressure Fluids, H.T.F.S. Design Report No. 34, Part 1—Summary of design recommendations and equations, Part 2—Critical reviews with design recommendations, AERE-R8157 and R8158, U.K.A.E.A., AERE, Harwell.
- Jackson, J. D. and Hall, W. B. (1980) Influences of buoyancy on heat transfer to fluids flowing in vertical tubes under turbulent conditions, 563-611, Turbulent Forced Convection in Channels and Rod Bundles, published by Hemisphere Publishing Corporation, USA (S. Kakacs and D.B. Spalding, Eds.)
- Krasnoschekov, E. A. and Protopopov, V. S. (1966) Experimental study of heat exchange in carbon dioxide in the supercritical range at high temperature drops, Teplofizika Vysokikh Temperatur, Vol. 4, No. 3.
- Petukhov, B. S. (1970) Heat transfer and friction in turbulent pipe flow with variable physical properties, Advances in Heat Transfer, Vol. 6, Academic Press, New York.