When a straight duct rotates about an arbitrary axis, rotation influences an internal pressure-driven flow via Coriolis and centripetal forces. These forces must be included in the momentum conservation equations in order to predict the resulting flow field as a precurser to the evaluation of heat transfer. Coriolis forces generate relative vorticity in the duct via a vector product coupling of the angular velocity and the flow field. In other words complex secondary flows may be generated. With unheated flow, the centripetal force field is hydrostatic. However, with heated flow, where the density of the fluid is temperature dependent, a centripetal buoyancy force is created analogous to natural convection in the earth’s gravitational field. The result of this is a mechanism which causes the warmer fluid (i.e., less dense) to move towards the axis of rotation. Again this will modify the nonrotating flow field and the heat transfer. A detailed description of how Coriolis and centripetal buoyancy terms may be incorporated into the momentum conservation equations is given by Morris (1981).
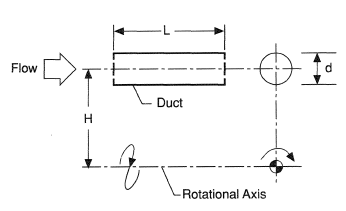
Although an infinite variety of rotating duct systems may be envisaged, reflecting the relative location of the duct to the axis of rotation, two important configurations have been seriously researched. These are commonly referred to as "parallel-mode" and "orthogonal-mode" rotation, respectively. With parallel-mode rotation the axis of the duct is parallel to, but displaced from the axis of rotation. Similarly, with orthogonal-mode rotation the axis of the duct and the axis of rotation are mutually perpendicular. In this entry heat transfer with parallel-mode rotation will be discussed. The case of orthogonal-mode rotation is discussed in the previous entry.
Figure 1 shows a typical straight duct rotating in the parallel-mode. Theoretical and experimental studies of heat transfer with this geometry have been extensively reviewed by Morris (1980) for laminar and turbulent flow and readers are referred to this text for full details. A brief summary of heat transfer data for circular-sectioned ducts follows by way of illustration of the general results.
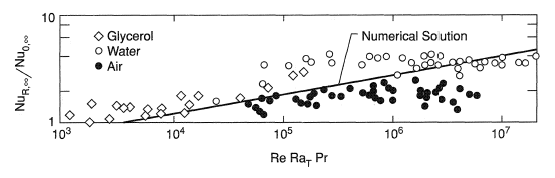
With developed laminar flow, a numerical solution for the Nusselt Number for the special case of very high Prandtl Numbers, Woods and Morris (1981), has been shown to be quite satisfactory even when applied to fluids with a Prandtl number as low as unity. Figure 2 shows a comparison of this high Prandtl number solution for heat transfer enhancement with experimental data obtained with glycerol, water and air. In this context enhancement is defined as the ratio of the developed Nusselt number with rotation, NuR,∞ with the stationary counterpart, Nuo,∞. This figure is recommended for assessing the effect of rotation with gases and liquids. Note that the effect of Coriolis force vanishes identically and rotation influences heat transfer via a centripetal buoyancy mechanism alone. The enhancement in heat transfer relative to the stationary case is dependent on the product of the through flow Reynolds Number, Re, a rotational Rayleigh number Rar, (which uses the product of the axial wall temperature gradient and the tube radius as a characteristic temperature difference in the customary definition) and the Prandtl number, Pr.
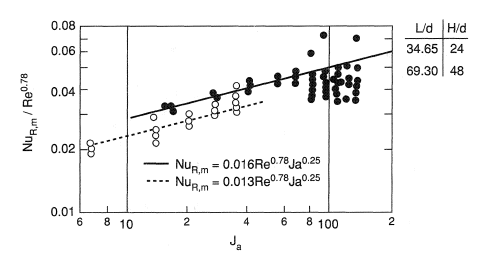
With developing flow, Coriolis forces are produced due to an interaction between the axial velocity gradient and the rotation. In this region, when the heating rates are moderate, buoyancy probably has a lesser influence and rotation may be quantified nondimensionally in terms of a rotational Reynolds number, Ja, (Ωd2ρ/4η) which may be thought of as a ratio of Coriolis to viscous forces. Morris and Woods (1978) have presented experimental data for two parallel-mode rotation geometries and recommended the following empirical correlations for the mean rotating Nusselt number, NuR,m


These equations were based on experiments with Ja values up to 150. At high rotational speeds, where buoyancy will become more important, it is not expected that these correlations will be particularly good. Figure 3 compares the actual test data with these correlations. Further details are available from Morris (1981).
With turbulent flow rotation still modifies the flow field to produce heat transfer enhancement. Nakayama (1968) used a momentum integral analysis to calculate developed turbulent Nusselt number and the following equations for determining this enhancement in heat transfer were proposed.
Case 1: Gas-like fluids with Pr close to unity.

where
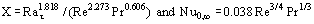
Case 2: Liquid-like fluids with Pr > 1
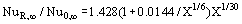
where

As with laminar flow, the effect of buoyancy has been found to be small in the turbulent entrance regions, see Morris (1981).
A relatively small number of experimental studies have been reported for air and Morris and Woods (1978) proposed the following correlation, very similar to that suggested for laminar flow, with which to estimate the mean rotating Nusselt number:

Figure 4 compares this equation with their actual experimental data. The data appears to be relatively insensitive to the aspect ratio of the tube and also the eccentricly. There is evidence, however, that this equation can overpredict the enhancement in heat transfer when compared to some data, see Morris (1981).
REFERENCES
Nakayama, W., (1968) Forced convective heat transfer in a straight pipe rotating about a parallel axis (turbulent region) Int. J. Heat Mass Trans., 11, 1185. DOI: 10.1016/0017-9310(68)90034-3
Morris, W. D. and Woods, J. L. (1978) Heat transfer in the entrance region of tubes that rotate about a parallel axis, J. Mech. Eng. Sci., 20–6, 1185 .
Morris, W. D. (1981) Heat Transfer and Fluid Flow in Rotating Cooling Channels, Research Monograph, Research Studies Press, A Division of J, Wiley and Sons, Ltd, ISBN 0471101214, 1–228.
Woods, J. L., and Morris, W. D. (1980) A study of heat transfer in a rotating cylindrical tube., Trans. A.S.M.E., J. Heat Trans., 102, 4, 612.
References
- Nakayama, W., (1968) Forced convective heat transfer in a straight pipe rotating about a parallel axis (turbulent region) Int. J. Heat Mass Trans., 11, 1185. DOI: 10.1016/0017-9310(68)90034-3
- Morris, W. D. and Woods, J. L. (1978) Heat transfer in the entrance region of tubes that rotate about a parallel axis, J. Mech. Eng. Sci., 20–6, 1185 DOI: 10.1243/JMES_JOUR_1978_020_057_02.
- Morris, W. D. (1981) Heat Transfer and Fluid Flow in Rotating Cooling Channels, Research Monograph, Research Studies Press, A Division of J, Wiley and Sons, Ltd, ISBN 0471101214, 1–228.
- Woods, J. L., and Morris, W. D. (1980) A study of heat transfer in a rotating cylindrical tube., Trans. A.S.M.E., J. Heat Trans., 102, 4, 612.