"Risk" and related terms, such as "risk assessment", "risk estimation", "risk evaluation" and "risk analysis" do not have universally agreed definitions, although there is a measure of consensus as to their meaning. A useful glossary and discussion on the use of the terms are given in an HSE document1. The glossary draws heavily upon a booklet published by the Institution of Chemical Engineers2 and The Royal Society Study Group (RSSG) on Risk Assessment3. The Institution of Chemical Engineers definition of risk is: "The likelihood of a specified undesired event occurring within a specified period or in specified circumstances. It may be either a frequency (the number of specified events occurring in unit time) or a probability (the probability of a specified event following a prior event), depending on the circumstances." This parallels the common usage definition.
It follows that to describe fully a risk it is necessary to
specify the event or outcome of interest,
estimate the probability of the event or outcome and, possibly,
estimate the severity or magnitude of the outcome or consequences.
Examples of risk are the probability of all-engine failure in an aircraft during a given flight, the frequency of toxic release from a chemical plant, the loss of power steering in a car when cornering or the probability of a major radioactive release from a nuclear power station.
As noted by HSE4 risk should not be reduced to a single quantity and its components need to be separately identified. There are examples in the literature, however, when the term "risk" is specifically defined by combining consequences with their probability.
The HSE1 also observes that "risk assessment" is a term used by both The Institution of Chemical Engineers and the RSSG to mean a process that includes the estimation of risk and a determination of the significance of the estimated risks. Significance is determined either by those most likely to be affected or by those making political decisions. The RSSG suggests the terms "risk estimation" and "risk evaluation" for the two parts of the process.
When the risk in question is one which causes harm, then it may either be to an individual, and termed "individual risk", or to the population, when it is termed "social-" or "societal risk". An individual risk can be expressed as an annual probability of death, or of contracting a disease. Societal risk is often expressed as the relationship between frequency and the number of people experiencing various specified levels of harm.
In the UK, the topic of risk evaluation (sometimes termed "risk appraisal") was debated at the Sizewell "B" Public Inquiry and one of the Inspector’s recommendations was that the HSE should formulate and publish guidance on the tolerable level of risk. This led to the publication of the HSE document4 which considered risks from nuclear and nonnuclear industries. The topics of risk evaluation and criteria to be applied are, however, outside the scope of this article.
This article is limited to estimation. When the estimate is quantified it is common to refer to it, in the nuclear industry, as a probabilistic safety assessment, PSA, or probabilistic risk assessment, PRA, and in the nonnuclear industry as a quantitative risk assessment, QRA. Whatever term is used the methods of analysis are the same.
Risk estimation or analysis is a process of forecasting the likelihood or probability of future events using data from previous events and/or details of the design of the plant in question. At its simplest level it can be the estimation of the unreliability of essential equipment. Reliability techniques have been under development for most of this century particularly in the aircraft and defence industries. However, since the 1970s the nuclear industry has taken the lead in developing risk analysis techniques. An early example was NRC’s Reactor Safety Study5 in which the probability of nuclear accidents and their consequences were estimated. Since then, probabilistic techniques have been used as part of the design process, as at Sizewell "B" for example, and as an aid to determining the acceptability of a given design or design change.
Failure modes and effects analysis (FMEA)
Event tree analysis
Fault tree analysis
The first step in any analysis, however, is to set down details of the overall plant, possibly in functional block diagram form if the system is complex. In a functional block diagram each part of the plant carrying out a particular function is represented by a single building block, the diagram then showing the interrelationships between the various blocks. All activities and processes need to be understood including details of any protective features.
The next step carefully and systematically identifies all the potential hazards and all the ways that the hazard can be generated. FMEA can be used to determine the initiating events or causes which could lead to the hazard. The technique is described as "bottom-up" since individual failures are traced forward to the final effect.
The results of an FMEA are summarized in truth or decision tables. The results are categorized according to their severity and estimates obtained of their probability of occurrence. This enables priorities for corrective action to be undertaken at the design stage. In practice, however, FMEA is primarily used to determine the effect of component failures, whether electrical, mechanical or structural, on a single system and not on the whole of a complex plant. The significance of failure of each component is then studied in turn. FMEA is an effective way of identifying all single faults which could cause system failure.
The event tree approach is used on a complex plant and is similar to an FMEA in that all possible sequences, following any postulated initiating event, are constructed. It is often convenient to group together similar initiating events. A simple event tree can be illustrated by considering the example shown in Figure 1.
Figure 1 represents a hypothetical fire protection system provided to extinguish any fire which might occur in a particular room in a building. Two electric pumps are provided to deliver water to a sprinkler system through an electrically operated valve. Water is taken from a reservoir. An automatic fire sensing system starts the pumps. The design intent is that one pump suffices. In this example the nonreturn valves in the system are assumed always to work. As a further line of defence to stop any fire spreading and causing extensive damage outside the room a fire door is provided, electrically driven, but manually operated. The fire door and the sprinkler system are each assumed to be 100% effective if they operate. Note, the example is not meant to be representative of any practical arrangement. One way of drawing the corresponding event tree is shown in Figure 2.
Along the top are listed all the items which should work. Starting with the initiating event, the fire, the first question asked is whether the automatic fire sensing system has worked. If it has then that is a success and the branch continues straight across; a step down indicates failure. Each branch then leads to a further question. The top branch leads do the question "does the spray system work?" The answer "yes" leads straight across; the answer "no" is represented by the branch which steps down. In this way is developed a tree of all possible sequences. In this example, the sequences whose end points are marked with a circle are deemed a success, although any success states claimed have to be demonstrated by calculation or other evidence. Those with a cross are failures. The probability of failure at each branch could also be added and hence the probability of each sequence evaluated. The total probability of failure is then obtained by summing all the failure sequence probabilities. In this example the failure probability of the overall spray system has to be input; this can be obtained from a fault tree analysis or, if desired, the event tree can be expanded to represent individual components. In general, the event tree is particularly useful in identifying those sequences which have to be shown by subsequent analysis to be acceptable because of their high probability.
Event trees, however, are usually constructed at a level with systems represented by blocks. Care has to be exercised to ensure that dependencies are correctly represented. In the example shown, if electrical failure is the main cause of spray system failure then it would equally stop the fire door from being closed, and an optimistic result could occur if the two events were assumed unrelated. The problem could be overcome by giving the question of electrical failure its own branch point in the tree. Dependencies are, however, automatically taken into account in the fault tree approach discussed later.
It may be, however, that the consequences are not defined in such a simplistic way as in the above example. Sequences are continued until any risk is fully identified. In the case of a chemical plant or nuclear power station the risk to be established could be the risk of death to an individual, or societal risk from a release of toxic chemicals or radioactive material. The aim of any risk analysis would be to show that any residual risk was sufficiently low as to be deemed tolerable. Methods of analyzing the probability of release of harmful releases are specific to particular industries.
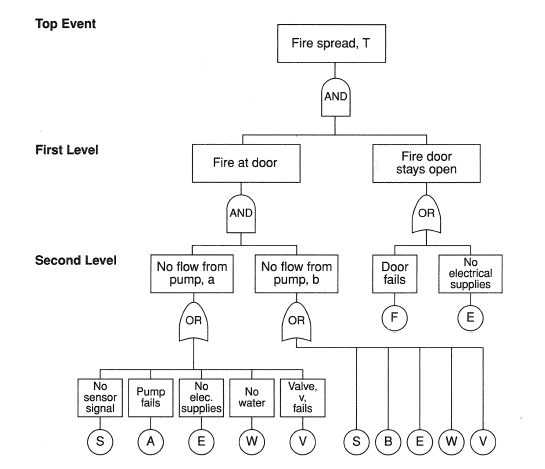
The fault tree approach treats any problem in a "top-down" manner. Whereas event trees identify a range of possible outcomes, fault trees identify ail contributors towards one specified outcome—the "top event". It is a logic diagram used to determine how a defined risk can occur either at the component level or at the system level. Consider again the system shown in Figure 1. Using capital letters to designate failure states a fault tree can be drawn for this system as shown in Figure 3, using symbols based upon those used in the NRC study5. The top event is the event we are interested in—the possibility of fire spread outside the equipment room. The AND gate underneath shows that the top event will only occur if all the input events, namely, the fire door not having been closed and the sprinkler system having failed to extinguish the fire. The AND gate at the next level down shows that the sprinkler system is only ineffective if there is no flow from pump "a" and no flow from pump "b". An OR gate defines the situation if one or more of the input events exist. Thus, the tree shows that the fire door remains open if either the electrical supply fails or if it fails because it jams (or because the operator failed to act). The branches end at a "basic" event which needs no further development because failure rate data are known or are assumed.
Using capital letters to represent the failure probability of the corresponding item, the probability of the top event, T, can be set down using the notation of Boolean algebra.6 The symbol for "and" is a dot, and for "or" the plus sign, +. This gives

This expression can be simplified by applying the logical rules of Boolean algebra6. For example, A.A = A = A + A.B and so on. In this way the expression is reduced to

Boolean reduction automatically takes into account the fact that loss of electrics is a contributing factor to the failure of a number of items. Component failure probabilities can be substituted to obtain system failure probability. (F.A.B), (F.W), (F.V), (F.S) and (E) are "Minimal Cut Sets" of components. In any minimal cut set all the component failures of which it consists must occur to result in system failure, but no other simultaneous failure is necessary. A "Non-minimal Cut Set" includes components whose failures can be tolerated. Boolean algebra identifies all the minimal cut-sets.
Only relatively simple systems can be analyzed by hand. Complex systems require the use of computer codes. Such codes can have a significant commercial value and new codes offering greater flexibility are continually appearing.
The value of any risk analysis obviously depends upon its completeness and whether all important initiating events and fault sequences have been identified. Certain aspects are difficult to model, such as the effect of human intervention, which may be either beneficial or harmful. When low probability risks are being evaluated the contribution from outside hazards such as aircraft crashing on the plant, earthquakes or extreme environmental conditions may be important. Failure rate data may not always be available or directly applicable and so judgements regarding its applicability may have to be applied. A particular difficulty can be the treatment of common cause failures. A common cause failure is an event which could cause simultaneous failure on a number of similar components and hence eliminate any benefit from redundancy or even diversity. A failure mode affecting similar components is sometimes referred to as a common mode failure. Methods for treating such failures are under continuous review.
It follows that there can be uncertainties associated with any risk analysis, and that judgement need to be exercised in using the results. As noted above, a risk calculation may be carried out at the design stage or on a completed plant or piece of equipment. The mere process of carrying out a risk assessment at the design stage is valuable, however, since it can identify ways of improving the design and reducing the risk.
REFERENCES
Health and Safety Executive, Risk criteria for land-use planning in the vicinity of major industrial hazards, 1989, ISBN 0 11 885491 7
Institution of Chemical Engineers, Nomenclature for hazard and risk assessment in the process industries 1985, ISBN 0 85 295184 1
Royal Society Study Group, Risk assessment, 1983, ISBN 0 85 403208 8.
Health and Safety Executive, The tolerability of risk from nuclear power stations, 1992, ISBN 0 11 886368 1.
NRC, WASH 1400 Reactor Safety Study.
Rueff, M. and Jeeger, M., (1970) Sets and Boolean Algebra. Allen and Unwin.
References
- Health and Safety Executive, Risk criteria for land-use planning in the vicinity of major industrial hazards, 1989, ISBN 0 11 885491 7
- Institution of Chemical Engineers, Nomenclature for hazard and risk assessment in the process industries 1985, ISBN 0 85 295184 1
- Royal Society Study Group, Risk assessment, 1983, ISBN 0 85 403208 8.
- Health and Safety Executive, The tolerability of risk from nuclear power stations, 1992, ISBN 0 11 886368 1.
- NRC, WASH 1400 Reactor Safety Study.
- Rueff, M. and Jeeger, M., (1970) Sets and Boolean Algebra. Allen and Unwin.