The convective transport of mass, momentum and heat normally occurs through a thin boundary layer close to the wall. The equations governing the transport of these quantities are analogous and are exact [Incropera & DeWitt (1990)] for laminar flow if the pressure gradient is equal to zero and the Prandtl Number (Pr) and Schmidt Number (Sc) are equal to unity. Under these conditions, their nondimensional convective transport coefficients are related by

where f is the Fanning friction factor, Re is the Reynolds Number, Nu is the Nusselt Number representing heat transfer and Sh the Sherwood Number representing mass transfer. Equation (1) is known as the Reynolds analogy, and enables the calculation of, for example, the heat transfer coefficient if either the friction factor or the mass transfer coefficient is known. (See also Analogy Between Heat, Mass and Momentum Transfer.)
For turbulent flow in a pipe or over a flat plate, the exchange of momentum, heat and mass occurs mainly by turbulent eddies in the bulk of the flow. However, very close to the wall, the exchange must occur by molecular diffusion across the velocity, temperature and concentration boundary layers, respectively. When Pr and Sc are equal or close to unity, the boundary layer thicknesses are roughly equal and Eq. (1) is applicable. When this is not so, which is often the case for liquids, proper account must be taken of the relative thicknesses of the boundary layers. A modified Reynolds analogy, also known as the Chilton-Colburn analogy, is found to be applicable under these conditions:
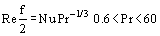

Equations (2) and (3) are applicable for both laminar and turbulent flow [Hewitt et al. (1994)].
REFERENCES
Hewitt, G. F., Shires, G. L., and Bott, T. R. (1994) Process Heat Transfer, McGraw-Hill.
Incropera, F. P. and DeWitt, D. P. (1990) Fundamentals of Heat and Mass Transfer, John Wiley and Sons.
References
- Hewitt, G. F., Shires, G. L., and Bott, T. R. (1994) Process Heat Transfer, McGraw-Hill.
- Incropera, F. P. and DeWitt, D. P. (1990) Fundamentals of Heat and Mass Transfer, John Wiley and Sons.